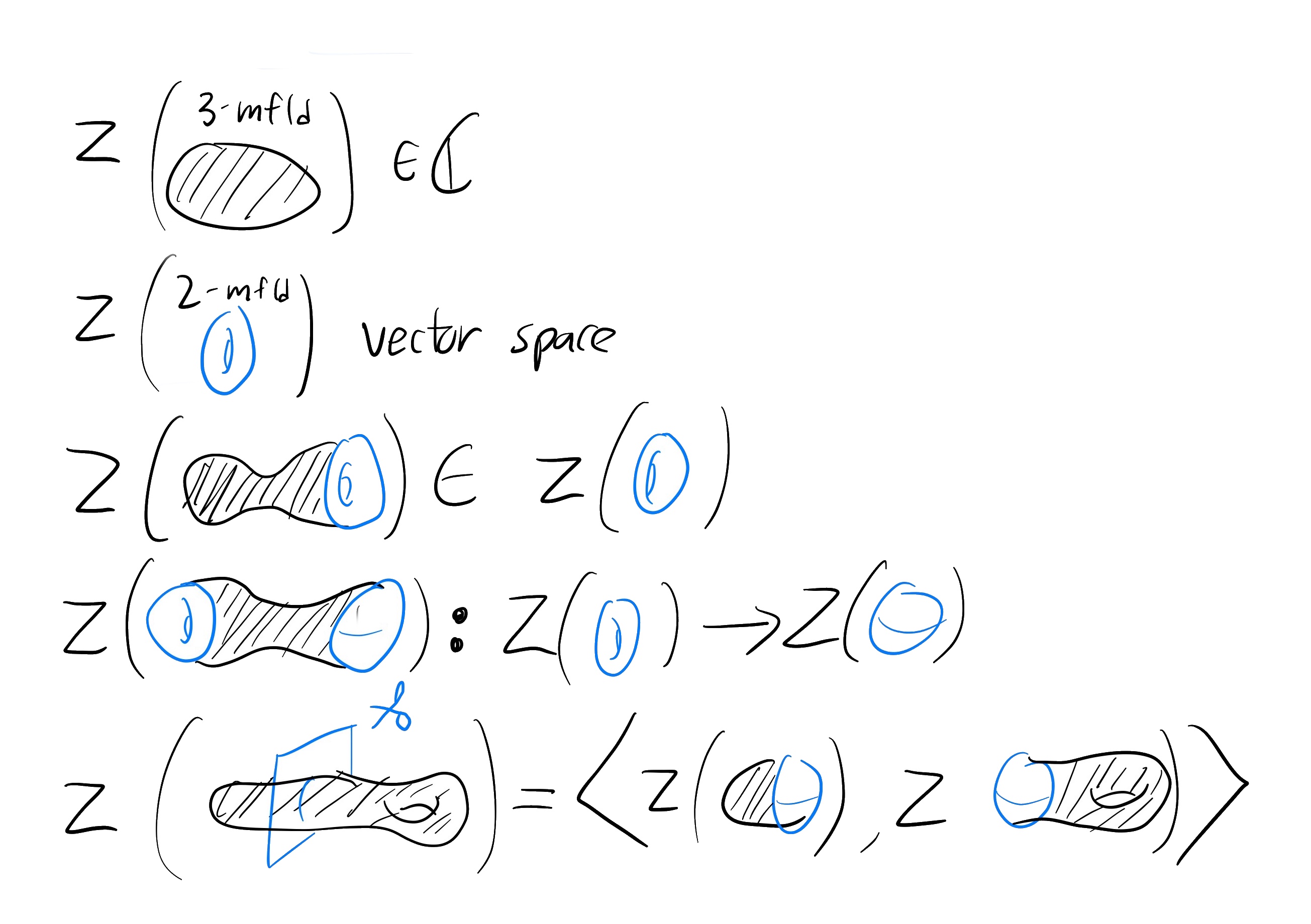Presentations
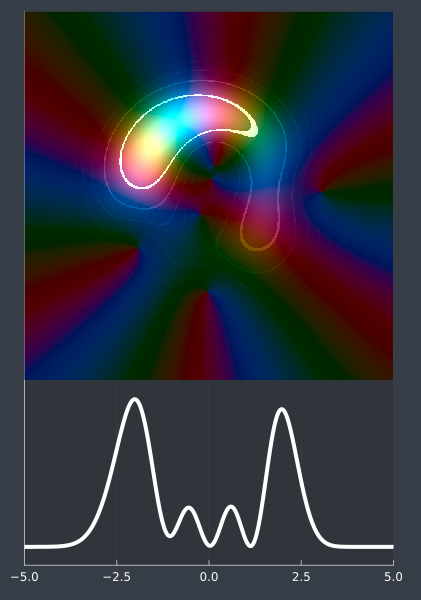
Uncertianty principles on Segal-Bargmann space
Summary:
The Fourier transform can be localized to encode the component frequencies of a signal at a particular time. This defines a function on a two dimensional “phase space”, with one dimension time and the other frequency. I will introduce my favorite phase space representation, the Segal-Bargmann transform, which takes a function on $L^2(\mathbb{R})$ and outputs a holomorphic function on $\mathbb{C}$. We will see how the phase space representation geometrically encodes the spectral properties of the original function, and build a dictionary between these two function spaces. Then, we manifest the uncertainty principle, stating that a holomorphic function in phase space cannot be too localized. First we will discuss coherent states, which have the largest possible $L^\infty$ norm for a fixed $L^2$ norm - a “minimal uncertainty” function. Then, we will prove a recent result of Nicola and Tilli, proving that the $L^2$ concentration of a holomorphic function on a set is maximized by coherent states on a ball.
Presented at:
- UC Berkeley student harmonic analysis, Fall 2025
🔗 Link to file
Packing stability, ECH capacity asymptotics, and simplicity of the Hamiltonian diffoemorphism group
Summary:
Recently, Oliver Edtmair posted to arxiv a pair of papers proving packing stability for all symplectic four-manifolds with smooth boundary. The proof relies on a refinement of an old theorem by Banyaga, stating that the group of hamiltonian diffeomorphisms is simple. I start by describing the ethos of ball packing problems, and discuss how symplectic ball packing controls the asymptotics of ECH capacities. Then, I introduce the the toy example from the introduction of Oliver’s paper, a class of manifolds where the simplicity of the Hamiltonian diffeomorphism group provides an explicit decomposition of the manifold into balls and polydiscs.
Presented at:
- UC Berkeley Symplectic Geometry Seminar, Fall 2025
🔗 Link to file
Cursed geometry with a pointless compass
Summary:
A pointless compass is a compass without a center. It can only make circles of a fixed radius passing between two points. Can you construct a perfect hexagon with only a pointless compass? The pursuit of the pointless hexagon led me to a perversion of sacred geometry, where symmetry is broken yet shapes still manage to close up.
Presented at:
- Many cheerful facts, Fall 2025
To draw a torus
Summary:
I spend a lot of time drawing pictures of surfaces, so I often wonder how to do so correctly. Shadows, shading, and reflections are all determined by the normal vector of the surface, and its orientation relative to the light and the viewer. The classical differential geometry of a surface is also entirely controlled by the normal vector, through the “Gauss map”. The curvature of the surface dictates how shadows fall, the shape of specular highlights, and even the number of highlights. We will reflect on how it is we draw a tours.
Presented at:
🔗 Link to file
How (not) to prove the Riemann hypothesis with quantum mechanics
Summary:
We will start with a roundtable discussion of this meme. One approach to the Riemann hypothesis is to find an operator whose eigenvalues are the zeros of the Riemann zeta function, then prove that operator is self-adjoint (The Hilbert-Ploya conjecture). I will tell you about a proposed way to construct such operators using symplectic geometry and quantization. This leaves us with a treasure hunt, a search for a hypothetical hamiltonian whose quantization solves the Riemann hypothesis. No one before, as far as I can tell, has used the edifice of contact homology to try to find this hamiltonian. Maybe there’s something we can do…
Presented at:
- Student Symplectic Summer Sessions, Summer 2025
🔗 Link to file
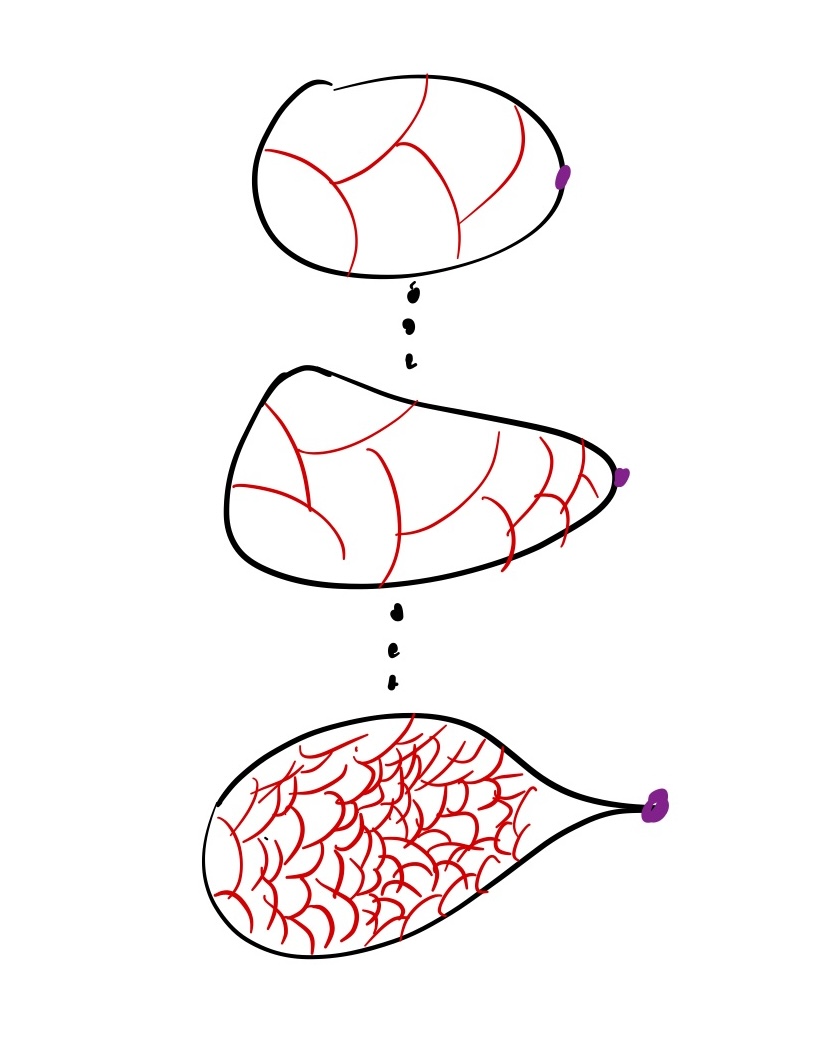
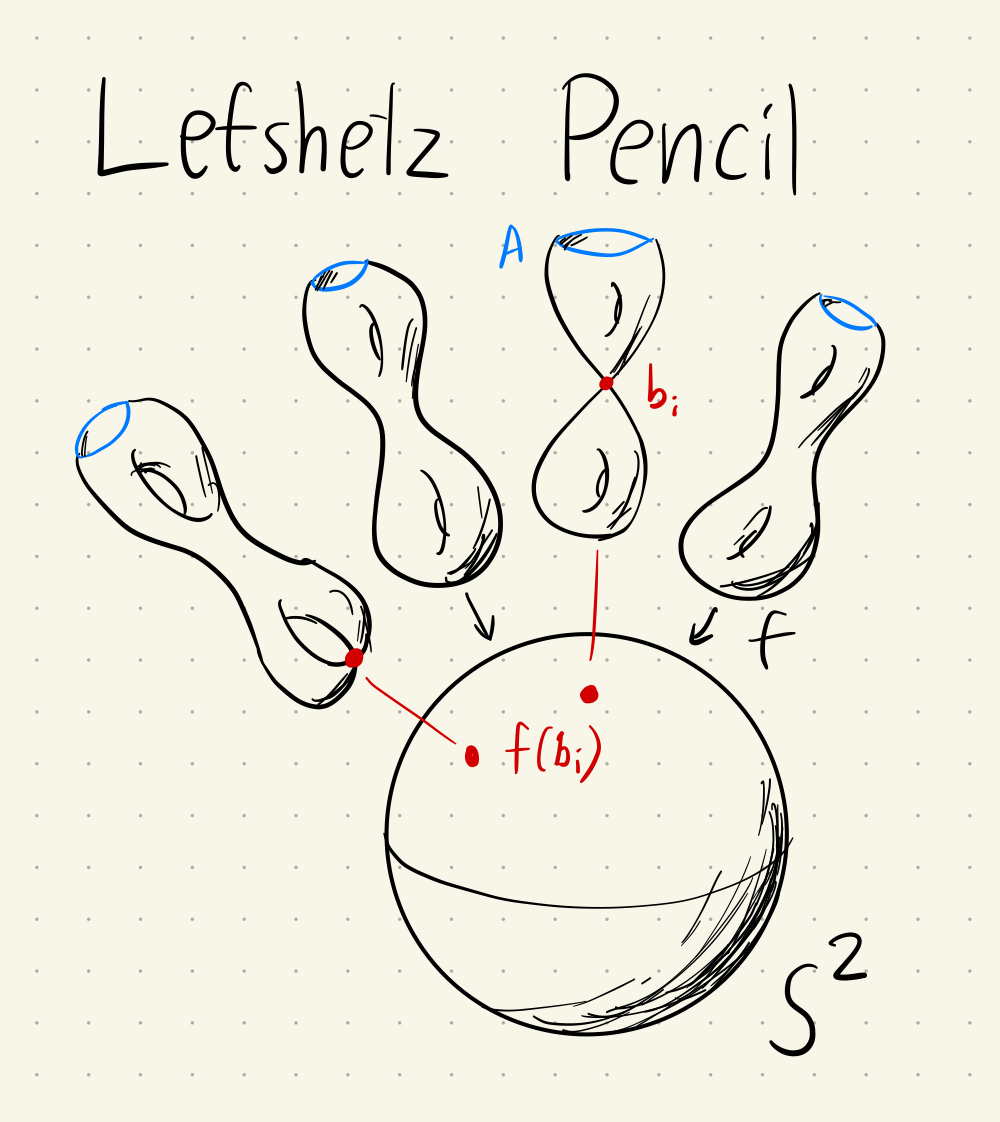
Asymptotic holomorphic methods in symplectic geometry
Summary:
In 1996, Donaldson proved that every closed symplectic submanifold has a closed symplectic submanifold. This paper was a Donaldson constructed these submanifolds as the zero set of certian sections which are very nearly holomorphic, called “asymptotically holomorphic section”. This result ushered in a new era of symplectic flexibility, borrowing topological constructions in Kahler geometry built from holomorphic section, and translating them into the symplectic category.
In this talk, I first sketch Donaldson’s construction of asymptotic holomorphic sections and symplectic manifolds. Then, I describe a number of topological structures which can be constructed from asymptotic holomorphic methods:
- Weinstein structures on the complement of Donaldson submanifolds
- Open book decompositions on contact manifolds
- Lefshetz pencils on symplectic 4-manifolds
- Maps from symplectic manifolds into projective space.
Presented at:
- UC Berkeley Symplectic geometry seminar, Spring 2025
🔗 Link to file
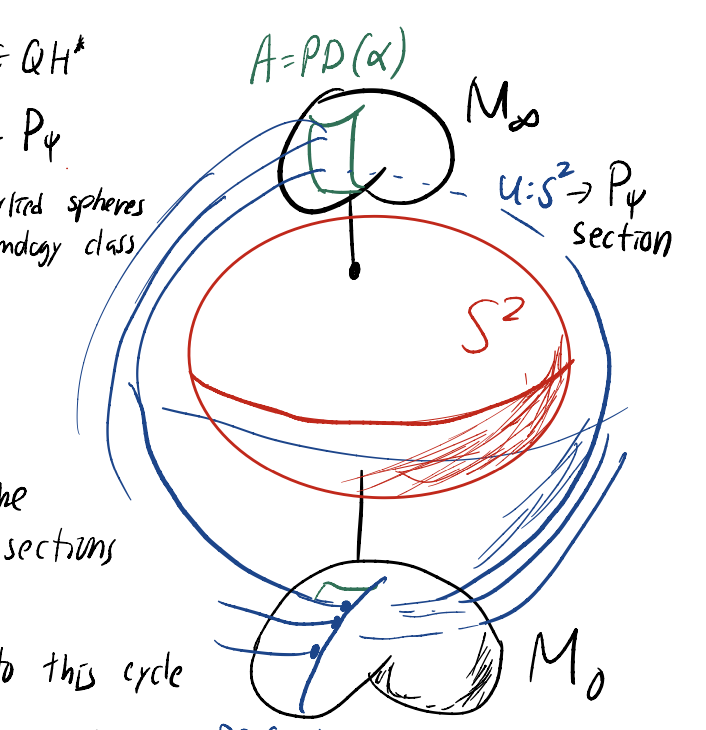
TQFT structure of Gromov-Witten theory and the Seidel representation
Summary:
First, I describe the TQFT structure of the topological sigma model with target a symplectic manifold. To a surface, the TQFT assigns gromov witten invariants. To a circle, it assigns quantum cohomology. To a point, it assigns the fukaya category. I describe the origin of quantum cohomology from the top down (by neck-stretching curves and using gromov-witten invariants) and bottom up (as the Hochschild cohomology of the Fukaya category).
Next, I discuss the Seidel representation. Given a loop $\Psi_t$ of hamiltonain diffeomorphisms, Seidel constructs a unit in the quantum cohomology ring, the “seidel element” $S(\Psi_t)$. An element of quantum cohomology is acted on by $\Psi_t$through multiplication by $S(\Psi_t)$. Seidel constructs $S(\Psi_t)$ by building a symplectic bundle over $\mathbb{P}^1$ with clutching function $\Psi_t$, then counting $J$-holomorphic sections. This is the first taste of the categorical action of Hamiltonian diffeomorphisms on the fukaya category.
Presented at:
- gauged TQFTs seminar , Spring 2025
🔗 Link to file
Matrix factorizations of quadratics and K-theory
Summary:
I describe the category of matrix factorization from a down-to-earth perspective. I argue why the matrix factorization category only sees the zero set of functions, and why the category is boring when 0 is not a critical level. Then, I’ll talk about matrix factorizations of quadratic polynomials. I describe why this category is isomorphic to the category of Clifford modules. Finally, I relate objects in matrix factorizations to topology, extracting topological vector bundle and a relative K theory class. Finally, I discuss the two-fold Knorrer periodicity for matrix factorizations, and explain how this is a categorized manifestation of Bott periodicity.
Presented at:
- UC Berkeley geometric representation theory seminar, spring 2025
🔗 Link to file
Vistas of mathematical illustration
Summary:
Seeing is believing. There are three axes of mathematical illustration: A picture can exposit mathematical ideas, aid in the discovery of new math, or be an avenue for artistic expression. We will take a whirlwind tour though several areas of the field, and get acquainted with the varied goals, themes, mediums, and lots and lots of pictures. Many contributors to this field have little formal math training. All you need is a new perspective and some visual flair.
Presented at:
- OURFA2M2: Online undergraduate research fair for the advancement and alignment of marginalized mathematicians.
🔗 Link to file
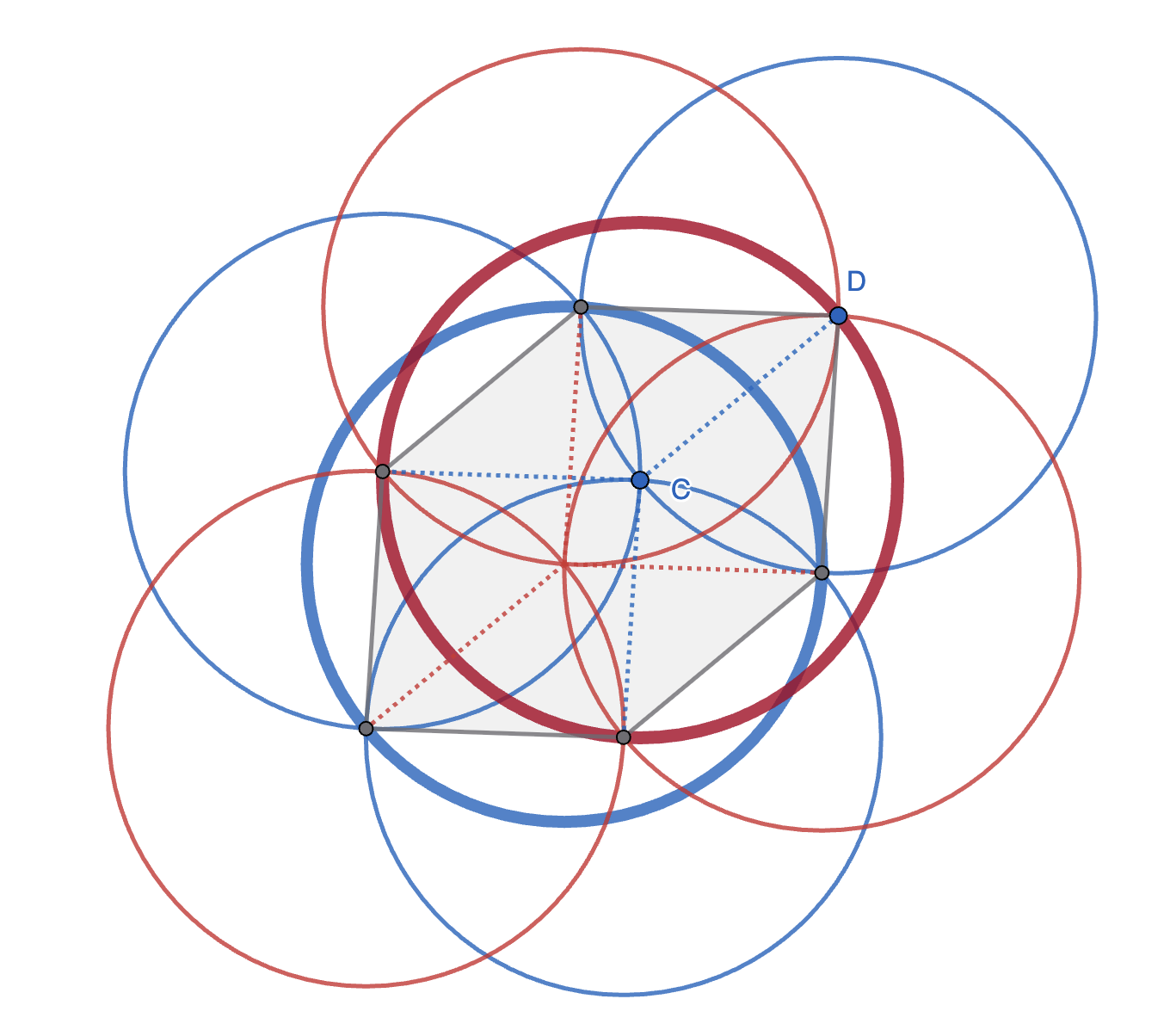
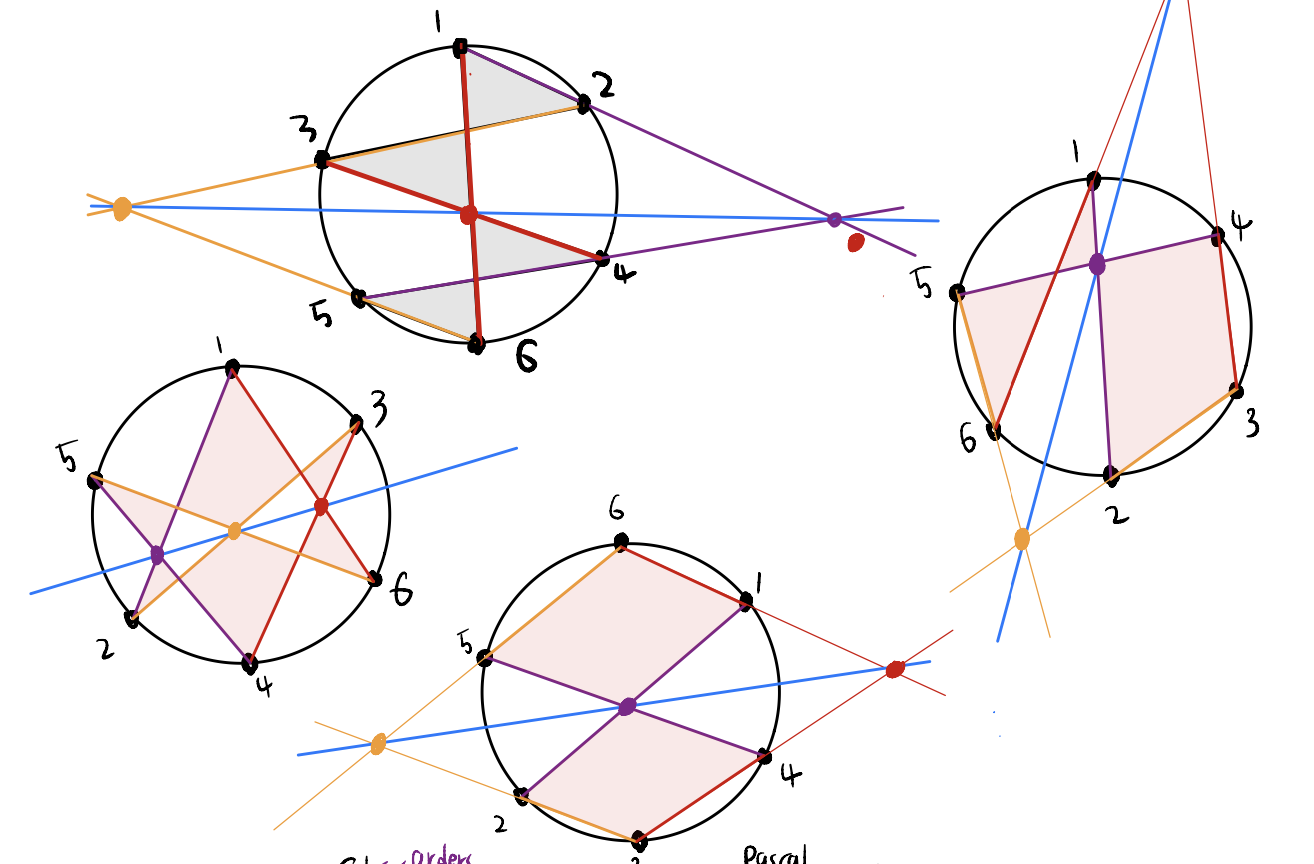
Elliptical Billiard tables
Summary:
Imagine playing billiards on an elliptical table. Can you hit the ball so that its trajectory is a triangle? Can every triangle appear as a billiards trajectory in some ellipse? As of 2024, the answer is Yes. The proof is a lovely tour of 18th century geometry, with a modern (1950’s) twist. I’ll prove this result, using a menagerie of facts about circles in and around ellipses. Digressions include: The Poncelet Porism, Pascal’s Hexagrammum mysticum, and Hartshorn’s beautiful representation of the moduli space of charge 2 instatons using poncelet ellipses
Presented at:
- UC Berkeley Many cheerful facts, spring 2025
🔗 Link to file
TQFTs and Gauge theory seminar
Summary:
Learning seminar on extended TQFTS and how to gauge them, Building up to Teleman’s 2014 ICM address
Presented at:
- UC Berkeley, spring 2025
Kempf-Ness theorem and quantization
Summary:
In symplectic geometry, groups act twice. When we take a symplectic reduction, first we demand the moment map equals zero, then we divide by the group. Instead we can form the symplectic reduction as the quotient by the complexified group. This is formalized by the Kempf-Ness theorem: Symplectic quotients equals GIT quotients.
Geometric quantization turns a symplectic manifold into a hilbert space. If we quantize a manifold with a G-action, quantization gives us a representation of G. This plays nice with symplectic reduction, as formalized in the Guilleman-Sternberg conjecture: The quantization of the reduced space is the G-invariants of the quantization.
These two mottos are the same idea in disguise.
Presented at:
- Student symplectic seminar
🔗 Link to file
Quasihamiltonain spaces and loop groups
Summary:
my favorite manifold is the moduli space of flat $G$-bundles on a Riemann surface. First I`ll construct it first as an infinite dimensional symplectic quotient, then with a finite dimensional model. The finite-dimensional construction looks a lot like symplectic reduction, with a lie group-valued moment map. This motivates the notion of a quasihamiltonian $G$-space, which have $G$-valued moment maps. Finally, I show quasihamiltonian $G$-space are equivalent to ordinary moment maps for loop groups.
Presented at:
- Student symplectic seminar
🔗 Link to file
Vignettes of caustic and catastrophes
Summary:
Caustics are focused concentrations of bent light, like the heart at the bottom of your coffee mug on a sunny day. The distinctive shapes of a caustic appear from more than just light. They lurk behind rainbows, the folds of cloth, and even the universe-scale structure of galaxies. These are all explained by a unifying geometric theory. I will share the geometry of caustics with a series of vignettes. First, we see how light folds inside a rainbow. Next, we tour the menagerie of caustics: cusps, swallowtails, butterflies, and more. Finally, we witness the rise and fall of catastrophe theory, a now-passe field that promotes caustics to a fundamental role across science.
Presented at:
- University of San Francisco Undergrad Colloquium
🔗 Link to file
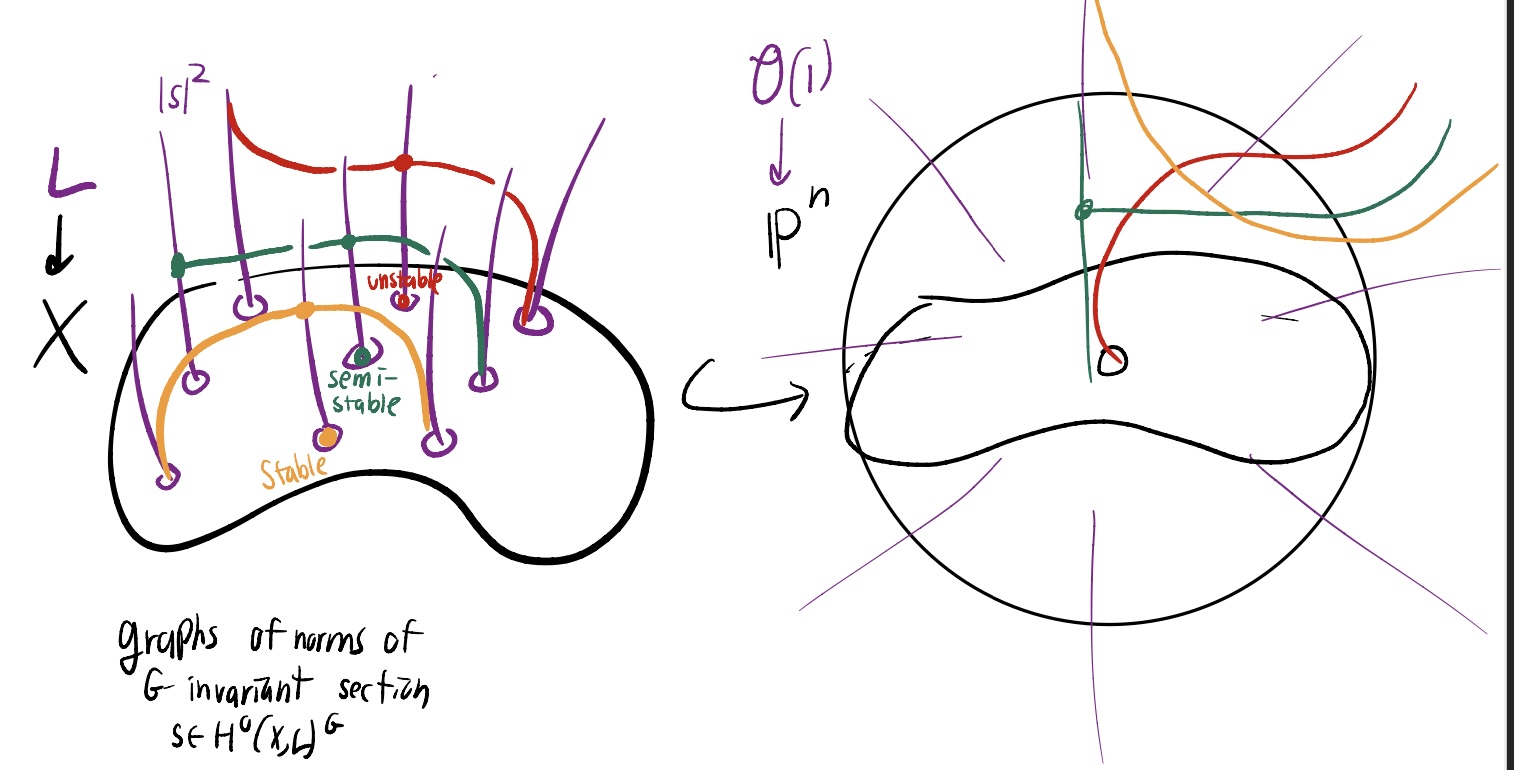
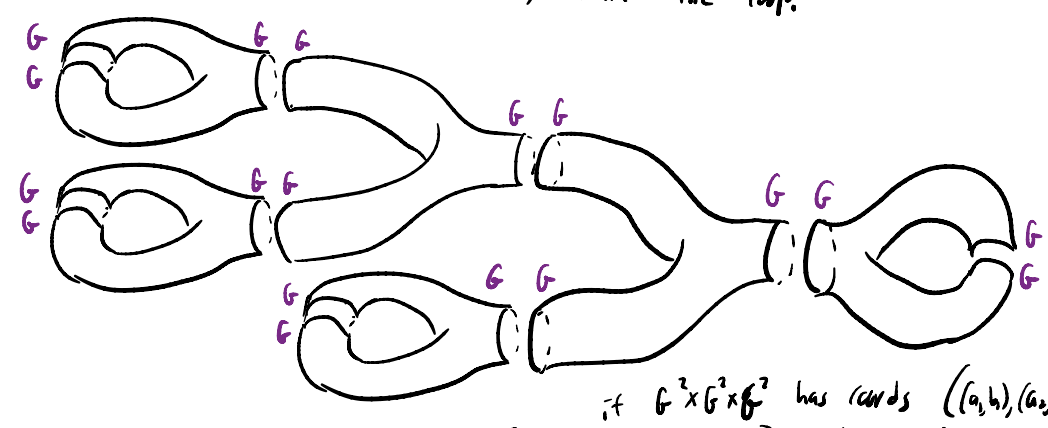
The Biran decomposition
Summary:
There is a clever way to split apart $\mathbb{C}$ into regions of equal area, using the morse theory of holomorphic functions. This is the first instantiation of a general procedure called the Biran decomposition. The symplectic structure of a Kahler manifold decomposes into two pieces: A symplectic disc bundle over a hyperplane section, and an isotropic skeleton. This Biran decomposition is a symplectic refinement of the Lefshetz hyperplane theorem. The proof uses the morse theory of the norm squared of a holomorphic section of the prequantum line bundle. We will use this to prove some lagrangian barrier phemonena. For example, every symplectic ball of radius $1/\sqrt{2}$ embedded in $\mathbb{C} \mathbb{P}^n$ interesects $\mathbb{R} \mathbb{P}^n$
Presented at:
- Student symplectic seminar
🔗 Link to file
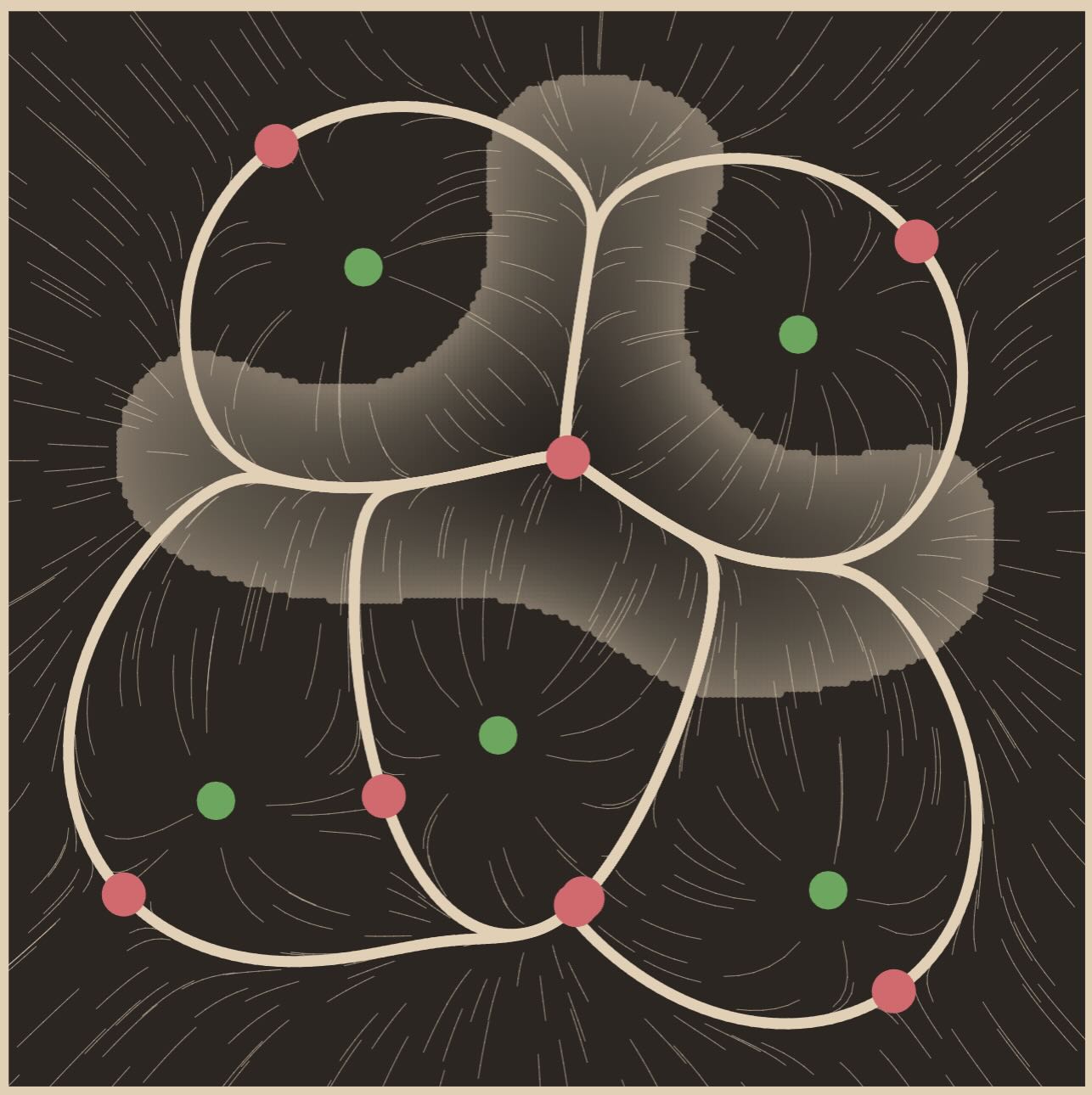
Symplectic geometry for classic curves and surfaces: The Caratheodory conjecture
Summary:
We call a point on a surface in $\mathbb{R^3}$ umbilic if both its principal curvatures are equal. The Carathedory conjecture, circa 1920s, posits that every topological sphere, embedded convexly in $\mathbb{R^3}$, has at least two umbilic points. I will discuss a (controversial) purported proof of the Carathedory conjecture using symplectic geometry and J-holomorphic curves, due to Guilfoyle and Klingenberg. This involves thinking of a surface though its congruence of normal lines, which traces out a lagrangian in the moduli space of lines in $\mathbb{R^3}$. The umbillic points are exactly the complex points of the lagrangian.
Presented at:
- Student symplectic seminar
🔗 Link to file
Manifesting Mathematical Worlds in Digital Art
Summary:
How do you visualize something which doesn’t fit on a page, like a high dimensional space or an entire field of math? You lie and cheat, use shortcuts and shorthand. In this talk, I’ll share my favorite tips and tricks for bringing math to life in digital painting.
Presented at:
🔗 Link to file
Abelian Chern-Simons theory
Summary:
I describe how to quantize Chern-Simons theory for an abelian gauge group. In particular, I describe the Hilbert space which Chern-Simons assigns to a surface. I follow the geometric quantization procedure, where the Hilbert space is the space of holomorphic sections over the moduli space of line bundles. I describe this space explicitly using theta functions. Next, I describe how the quantization depends on the choice of complex structure on our surface. I describe the projective connection on the bundle of Hilbert spaces, and its relationship with the heat equation.
Presented at:
🔗 Link to file
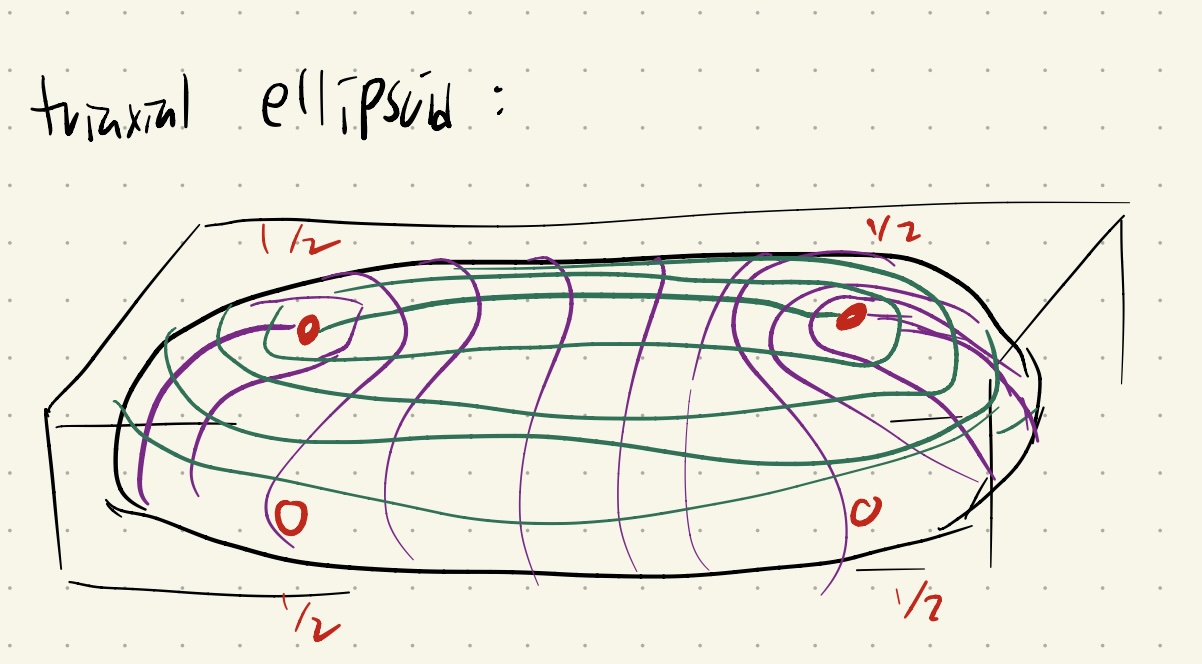
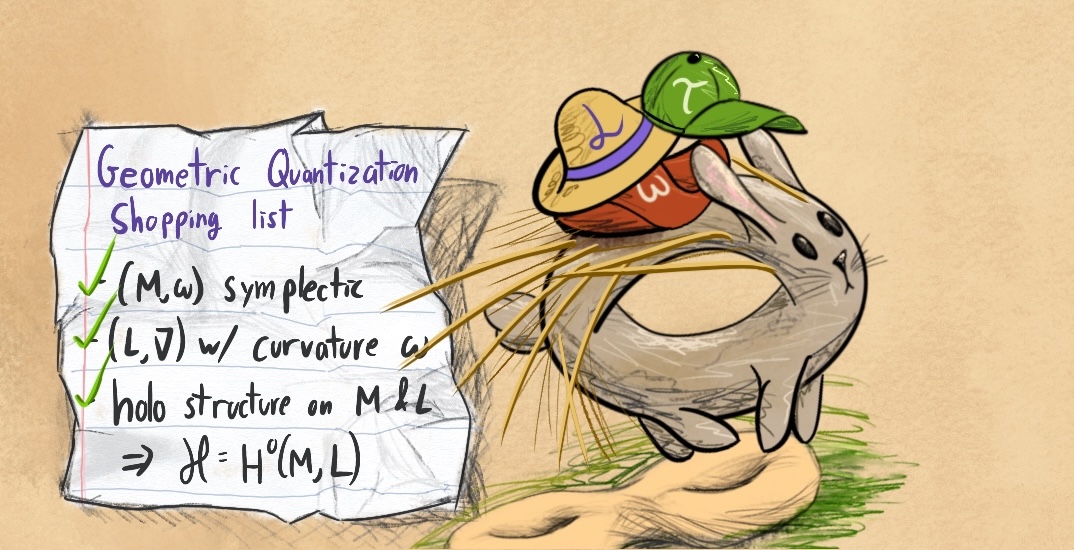
Geometric quantization of coadjoint orbits
Summary:
I explain the process of geometric quantization, which constructs a vector space from a symplectic manifold. Applied to a coadjoint orbit of a compact group, this gives the associated irreducible representation promised by the orbit method. This provides another perspective on the Borel-Weil theorem. Along the way, I explain coadjoint orbits combinatorially in terms of a torus action and its moment map, and phrase quantization using this description.
Presented at:
- UC Berkeley Orbit method Learning seminar, fall 2023
🔗 Link to file
Chern-simons theory and the Jones polynomial
Summary:
Knots were born from Kelvin’s vortex theory of atoms. This was a bold (if ultimately misguided) attempt to quantize physics through the topology of knots. Following the steady march of mathematical progress, knots strayed far from their physical roots. I describe a curious rondevouz in the 1980s, when a modern incarnation of Kelvin’s vortex theory once again spurred knot theory, now through the jones polynomial. I give two talks summarizing this story, and Witten’s paper on quantum field theory and the jones polynomial.
Presented at:
- UC Berkeley Jones polynomial learaning seminar, fall 2023
🔗 Link to file
Understanding hamiltonian G-spaces through quantization
Summary:
Philosophically, quantization converts functions on symplectic manifolds to operators on Hilbert spaces in a structure-preserving way. A symplectic manifold carrying a structure-preserving \(G\)-action quantizes to a \(G\)-action on the Hilbert space, or a representation of \(G\). Using this, we can study representations through the geometry of symplectic manifolds. After outlining this philosophy, I describe a parallelism between symplectic manifolds and representations. Coadjoint orbits are irreducible representations, the moment map is a decomposition into irreducible representations. Constructions which engineer new representations become blueprints for building new symplectic manifolds. These constructions motivate hyperspherical varieties, the class of spaces starring in relative langlands duality
Presented at:
- UC Berkeley geometric representation theory seminar, fall 2023
🔗 Link to file
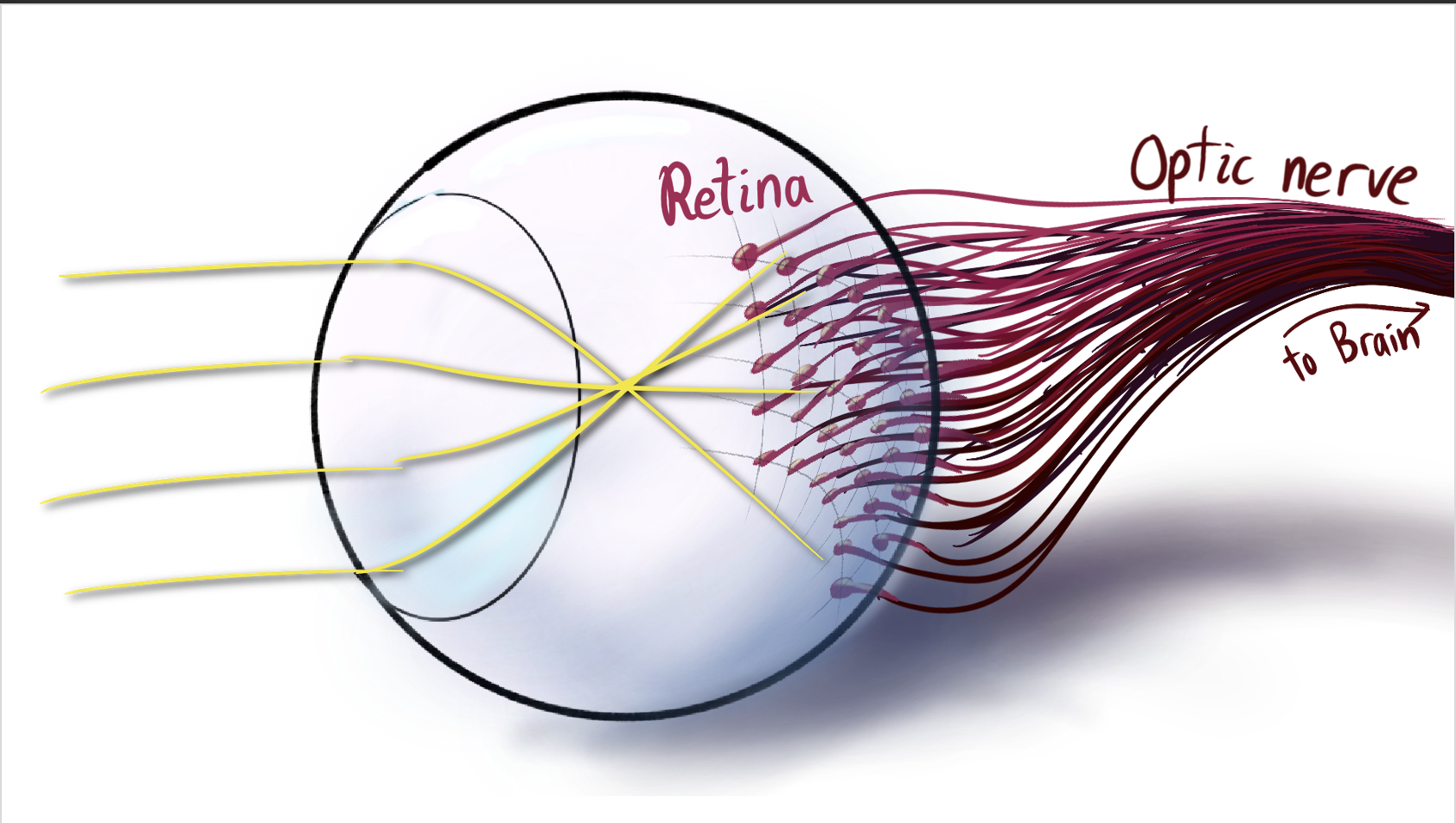
How we see with geometry
Summary:
When we see, the data from our eyes streams into the seemingly impenetrable jumble of neurons and synapses called our brain. In between, the signal passes through the visual cortex, a few layers of preprocessing which converts our visual field into abstract shapes. To do this, it seems evolution discovered differential geometry. First, the orientation of neurons in the visual cortex traces out a contact structure, a field of planes in R^3 tangent to no 2-dimensional submanifold. This automatically traces contours around everything we see. Second, the shape of the neurons themselves follow orbits of Euclidean and conformal symmetries, ensuring our perception is invariant under change of perspective. Together, this geometry will reveal itself to us through illusions and hallucinations.
Presented at:
- UC Berkeley Many cheerful facts, spring 2023
🔗 Link to file
Coloumb Branches reading seminar
Summary:
I organized a semester-long reading seminar on Coloumb branches. I gave talks here about superalgebras, supersymmetry in quantum field theory, hypertoric geometry, and abelian coloumb branches.
Presented at:
- UC Berkeley, spring 2023
Polygon moduli spaces
Summary:
The moduli space of polygons encodes how many ways you can bend the edges of a 3D polygon, ensuring the distance between adjacent points remains the same. In this talk, I gave people physical models of polygons, and had them figure out the moduli space up to rigid rotations. This reveals quite a lot of deep structure. Symplectic geometry, coadjoint orbits, toric geometry, and quiver varieties all come into play. We can even reframe the moduli space gauge theoretically as that of some flat connections on the punctured sphere. This web of equivalences make polygon spaces useful testing grounds. This is amplified when we pass to their hyperkahler analog, the hyperpolygon space, who connects with Nakajima quiver varieties and the moduli space of Higgs bundles.
Presented at:
- UC Berkeley geometric represenation theory seminar, Spring 2023
Hyperbolic string art
Summary:
I close my eyes, but all I see are strings. Stretch a line across a circle according to simple mathematical rules, and you get elegant patterns often dubbed “string art”. For example, connect each angle $\theta$ to the angle $2 \theta$, and the heart-shaped cardiod emerges. This talk chronicles my fourier into hyperbolic string art, a recontextualization of string art imagining the circle as the boundary of the hyperbolic plane, and the straight lines as hyperbolic geodesics. The patterns arising from natural hyperbolic transforms reveal the symmetries and geometry of hyperbolic space. With hyperbolic string art, we navigate the hyperbolic plane watching only the horizon, and visualize the moduli space of closed hyperbolic surfaces.
Presented at:
- UC Berkerly many cheerful facts, Fall 2023
🔗 Link to file
Link to sketch
Stick bombs
Summary:
Weave together 4 or 5 popsicle sticks in the right way, and you get a flat rigid pattern – until you drop it. The fast-released elastic energy shoots apart the popsicle sticks, producing a stick bomb. Join us as we try and discover the mathematics behind stick bombs, what makes them stay together and what makes them fall apart. Working together in groups, we’ll come up with Many of our own Cheerful Facts about tounge-depresser trajectiles :)
Presented at:
- UC Berkeley Many cheerful facts, fall 2022
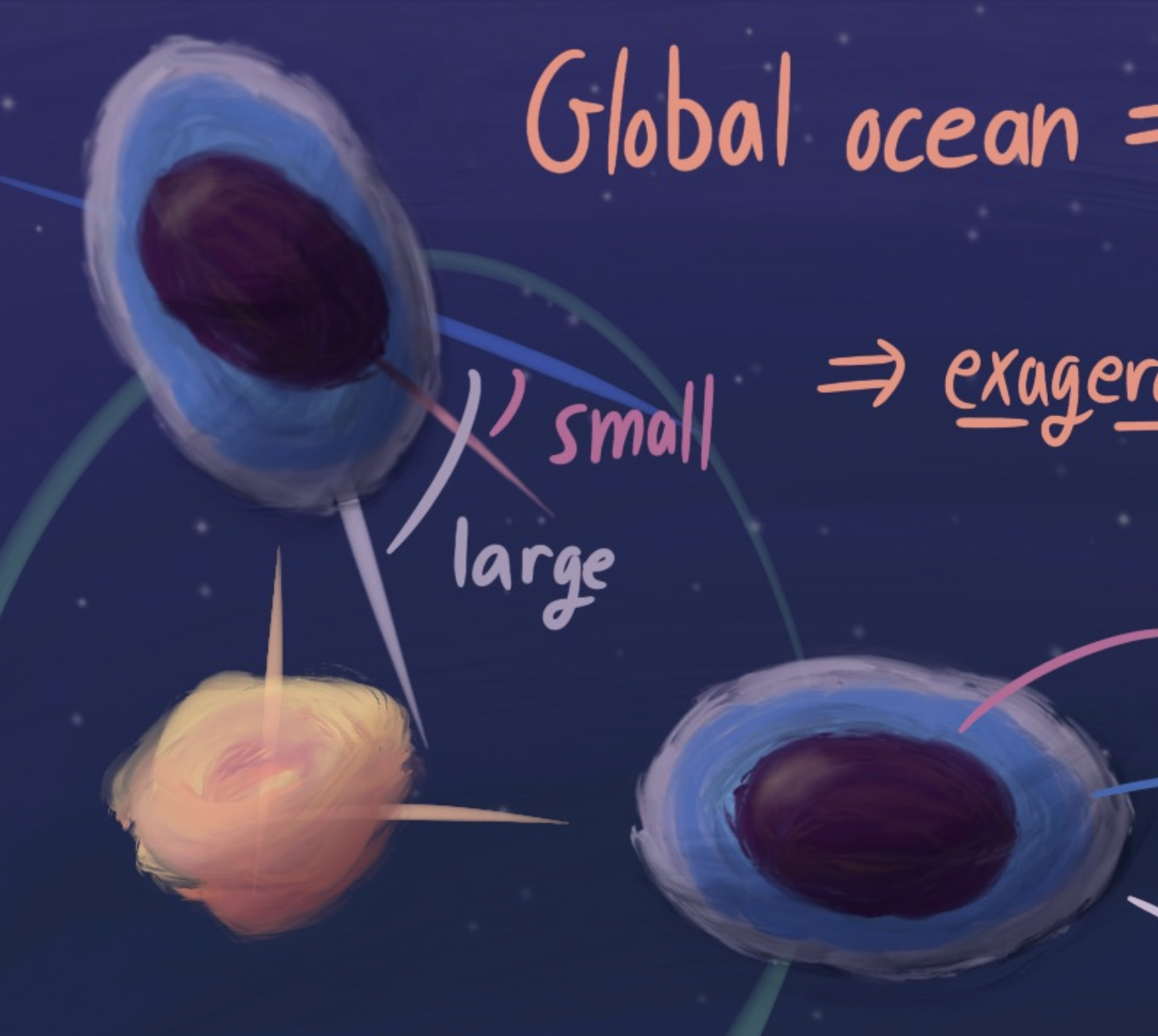
Enceladus and its ocean
Summary:
Not math. I explain how we know that Saturn’s moon Enceladus has a global subsurface ocean, following the paper ‘Enceladus measured physical libration requires a global subsurface ocean’ by Thomas et.al. In particular, I have a nice explination with pictures of libration and forced libration, and how we can use it to study planets.
Presented at:
- ASTR430, The Solar System, UMD, Spring 2021
🔗 Link to file
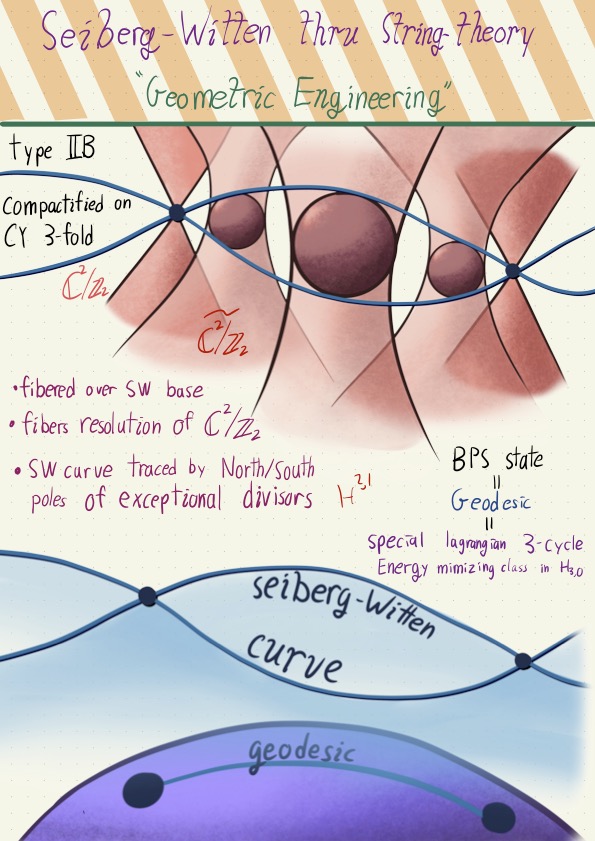
BPS states, Seiberg-Witten theory, and Integrable systems
Summary:
a trilogy of talks that all explore the power of BPS states in math and physics. First, I relate the BPS representations of supersymmetric algebras with BPS monopoles. Second, I go through Seiberg and Wittens solution for the low energy effective field theory of N=2, D=4 super yang mills. Vitally, they use the topological aspect of BPS states to pull back a lattice from the free theory to the whole vacuum moduli space, giving an integrable system. Third, I give a unified description of BPS states as variations of hodge structures, and discuss how various avatars of BPS states fit in to the story.
Presented at:
🔗 Link to file
The Dark Magic of Integrable Systems
Summary:
The nefarious physicists, a cult of symmetry, have gone too far this time. By constructing a theory with not 1, but 2 supersymmetric partners, they evoked the dark magic of integrable systems. Now they must clean up their mess. They leave gauge theory grove for Loui-ville, a humdrum town caught in the eternal cycles around the tori in an integrable system. Next they brave the soliton swamps, coming face to face with the Toad-a lattices and their waves of hopping toads. They escape the swamp through the spectral cemetery, where the spirits of long-passed integrable systems are chained to forever cover their Riemann surfaces. At last, they come upon the Seiberg-Witten summit, a fortress of spectral curves built by the supersymmetric theory they brought into the world.
Presented at:
🔗 Link to file
Topological recursion: For fun and profit
Summary:
How do rainbows relate to quantum gravity, random matricies, and WKB analysis? Im glad you asked. These all have underlying recursive formula, based on cutting up riemann surfaces into pairs of pants. These various types of ‘topological recursion’ were unified by Eynard and Orantin, relating each recursive structure to a spectral curve of a simple polynomial.
Presented at:
🔗 Link to file
Electromagnetism on a Riemann surfaces
Summary:
Maxwells equations have a very elegant formulation in terms of differential forms. As a U(1) gauge theory, the electromagnetic field is a connection on a U(1) principle bundle. These are equivalent to holomorphic line bundles! The moduli space of solutions to vacuum maxell’s equations on a riemann surface is the Jacobian. We can give much of classical Riemann surface theory a gauge-theoretic coat of paint. This observation, generalized to nonableian groups and noncompact groups, is the heart of the nonabelain hodge correspondence.
Presented at:
- MATH669, Riemann surfaces, UMD, Fall 2021
🔗 Link to file
Hyperbolic Band Theory Through Higgs Bundles
Summary:
Periodic crystals on the hyperbolic plane underlie an emerging bridge between condensed matter physics and algebraic geometry. Mathematically, hyperbolic crystals prompt us to study the spectrum of the hyperbolic laplacian plus a potential which is periodic under some hyperbolic lattice. Motivated by band theory, the space of functions splits into representations of the hyperbolic lattice, decomposing the spectrum into “bands” over the moduli space of such representations. Geometrically, these bands are the spectrum of the laplacian of a flat connection on the associated Riemann surface, graphed over the moduli space of such connections. After introducing this, I will discuss my own work (joint with Steve Rayan) incorporating Higgs bundles into the story. Higgs bundles enjoy a couple natural spectral-theoretic interpretations, first appearing from complex representations, and second encoding symmetries of the underlying hyperbolic lattice. Time permitting, I’ll daydream about how Higgs bundles might weave hyperbolic crystals into a web of ideas across mathematics and physics.
Presented at:
- Geometry and Mathematical Physics Seminar at the University of Saskatchewan
- JMM 2022 AMS Contributed Paper Session
- MSRI gauge theory graduate student seminar
🔗 Link to file
Higgs bundles and geometric structures
Summary:
An introduction to the theory of Higgs bundles and the nonabelian hodge correspondence. I emphasized the aspects related to geometric structures, in particular how the Hitchin section of SL(2,C) Higgs bundles gives hyperbolic structures.
Presented at:
- MATH848C, Geometric structures, UMD, Spring 2021
🔗 Link to file
Cobordisms and the Thom Spectrum
Summary:
In the first part, I give a whimsical introduction to cobordisms, what they do for algebraic topologists, and how they come up in mathematics. In the second, I construct the Thom spectrum associated to the cobordism cohomology theory, using the Pontryagin-Thom construction.
Presented at:
🔗 Link to file
Kahler Quantization and Physics
Summary:
Geometric quantization associates a Kahler manifold to a vector space of holomorphic sections of a line bundle. By taking higher and higher powers of the line bundle, there are more and more holomorphic sections. In the limit, each point on the manifold sits in CP infinity by the Kodira embedding. These are coherent states, acting as quantum analogous of a classical point particle. This strategy is very useful in pure Kahler geometry.
Presented at:
- MATH868C, Complex Geometry, UMD, Spring 2021
🔗 Link to file
Higgs bundles, Mirror symmetry, and Geometric Langlands
Summary:
This talk gives a summary of the Kapustin-Witten appraoch to the geometric langlands correspondence. This realizes geometric langlands as a duality between A-branes (langrangian submanifolds) on the moduli space of Higgs bundles with gauge group G, and B-branes (coherent sheaves) on the moduli space of Higgs bundles with the langlands dual gauge group G^L. This flavor of mirror symmetry arises from S-duality of an N=4 supersymmetric 4D gauge theory. On the Higgs bundles side, it comes from T-duality of the Hitchin integrable system.
Presented at:
🔗 Link to file
Lie's Theorem
Summary:
A short (~15 minute) exposition & proof of Lie’s theorem, which says that solvable Lie algebras act like upper triangular matricies.
Presented at:
- MATH740, Lie groups, UMD, Fall 2020
🔗 Link to file
The Riemann-Roch Theorem
Summary:
The Riemann-Roch theorem gives the number of linearly independent holomorphic sections to a line bundle. I explain morally why divisors should correspond to line bundles, and present the usual sheaf-theoretic derivation of Riemann-Roch. But to me, Riemann-Roch relates the solutions of differential equations to the genus, bridging analysis and toppology. This was my first intoxicating taste of the Atiyah-Singer index theorem
Presented at:
- MATH742, Geometric analysis, UMD, Fall 2020
🔗 Link to file
A and B models: The story of mirror symmetry
Summary:
This talk states mirror symmetry, framed as a conjecture about the equivlence of two frobenius manifolds. Two sorts of ‘topological twisting’ should give equivlent topological field theories. The first gives the A-model, which is a path integral counting holomorphic curves in a kahler manifold. The second gives the B-model, a Landau-Ginzburg theory whose physics depends on the singularity structure of a holomorphic function. Underlying both is the structure of a frobenius manifold– Mirror symmetry conjectures that its the same structure
Presented at:
- UMD RIT in geometry and physics, Fall 2020