Asymptotic holomorphic methods in symplectic geometry

Mar 2025

talk

Summary:

In 1996, Donaldson proved that every closed symplectic submanifold has a closed symplectic submanifold. This paper was a Donaldson constructed these submanifolds as the zero set of certian sections which are very nearly holomorphic, called “asymptotically holomorphic section”. This result ushered in a new era of symplectic flexibility, borrowing topological constructions in Kahler geometry built from holomorphic section, and translating them into the symplectic category.

In this talk, I first sketch Donaldson’s construction of asymptotic holomorphic sections and symplectic manifolds. Then, I describe a number of topological structures which can be constructed from asymptotic holomorphic methods:

• Weinstein structures on the complement of Donaldson submanifolds
• Open book decompositions on contact manifolds
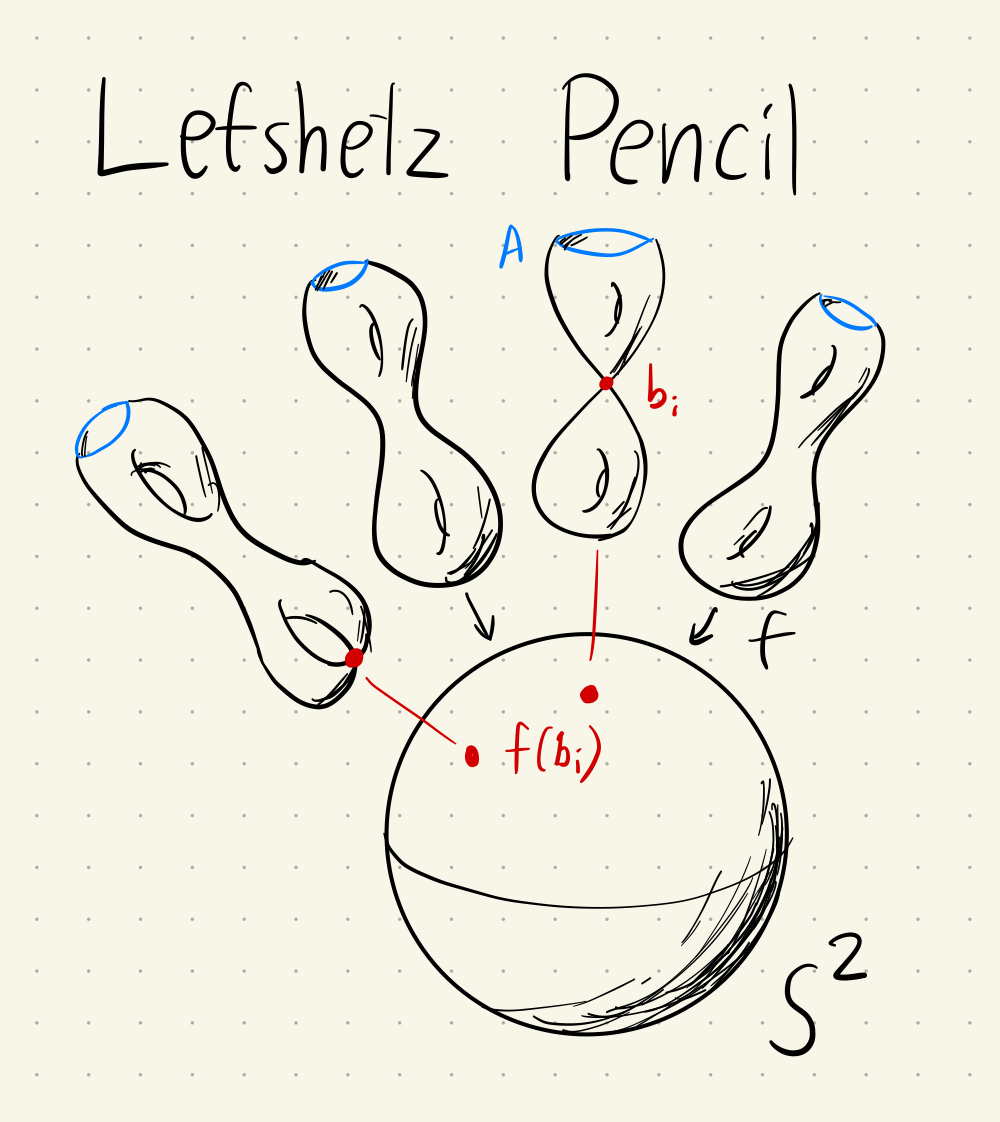
• Lefshetz pencils on symplectic 4-manifolds
• Maps from symplectic manifolds into projective space.

Presented at:

• UC Berkeley Symplectic geometry seminar, Spring 2025

🔗 Link to file

Sources

Donaldson submanifolds

Donaldson 1996, SYMPLECTIC SUBMANIFOLDS AND ALMOST-COMPLEX GEOMETRY

• Donaldson’s original paper, the main source for the first half of the talk. If you take the leap to read the paper, I recommend looking also at AUROUX, A REMARK ABOUT DONALDSON’S CONSTRUCTION OF SYMPLECTIC SUBMANIFOLDS, where they simplify donaldson’s argument to avoid subtitles in proving the quantitative sard’s theorem.

Topological applications

Open book decompositions

A. Ibort, D. Martínez-Torres, F. Presas, 2000, On the Construction of Contact Submanifolds with Prescribed Topology

• Extended Donadson’s submanifold theorem to the contact case

Emmanuel Giroux, 2003, Géométrie de contact: de la dimension trois vers les dimensions supérieures

• Proved the one-to-one correspondence between open books (up to stabalization) and contact structures. To construct an open book carrying a specific contact structure, Giroux applied the contact sub-manifold construction of A. Ibort, D. Martínez-Torres, F. Presas. Unfortunatly, this is in french and there’s no translation.

C. Caubel, A. Nemethi, P. Popescu-Pampu, 2004, Milnor open books and Milnor fillable contact 3-manifolds

• Describes explicitly the contact structure carried by the open book coming from a holomorphic function. Giroux then generalized this from the holomorphic to asymptotic holomorphic case.

Weinstein complements

Emmanuel Giroux, 2017, Remarks on Donaldson’s symplectic submanifolds

• Proves the complement of a Donaldson submanifold is Weinstein.

This is similar to the notion of a Biran decomposition on a Kahler manifold. I have notes and sources for this in the Biran Decomposition.

Lefshetz pencils

Donaldson, 1999, Lefschetz pencils on symplectic manifolds

• Origional source for construction of Lefshetz pencils on symplectic 4-manifolds

Projective embeddings

Aurorux, 2000, [Symplectic 4-manifolds as branched coverings of ℂℙ2]

• Constructed a map from a symplectic 4-manifold into $\mathbb{P}^2$, and proved that this gives a branched covering

David Borthwick, Alejandro Uribe, 1998, Nearly Kahlerian Embeddings of Symplectic Manifolds

• Constructed an embedding of sympletic manifolds into high dimensional projective space, such that the embedding is nearly isometric.