The Biran decomposition
Summary:
There is a clever way to split apart $\mathbb{C}$ into regions of equal area, using the morse theory of holomorphic functions. This is the first instantiation of a general procedure called the Biran decomposition. The symplectic structure of a Kahler manifold decomposes into two pieces: A symplectic disc bundle over a hyperplane section, and an isotropic skeleton. This Biran decomposition is a symplectic refinement of the Lefshetz hyperplane theorem. The proof uses the morse theory of the norm squared of a holomorphic section of the prequantum line bundle. We will use this to prove some lagrangian barrier phemonena. For example, every symplectic ball of radius $1/\sqrt{2}$ embedded in $\mathbb{C} \mathbb{P}^n$ interesects $\mathbb{R} \mathbb{P}^n$
Presented at:
- Student symplectic seminar
🔗 Link to file
Biran decomposition on $\mathbb{C}$
Let me tell you about a fun way to decompose the plane into regions of equal area. This procedure produces very blobby, organic looking shapes (See the image above). The procedure originated from symplectic geometry, but in dimension 2, it reduces to complex analysis and some morse theory.
Consider a function $f\in \mathcal{H}_k = HL_k^2(\mathbb{C})$, meaning $f$ is holomorphic and the following weighted $L^2$ integral is finite:
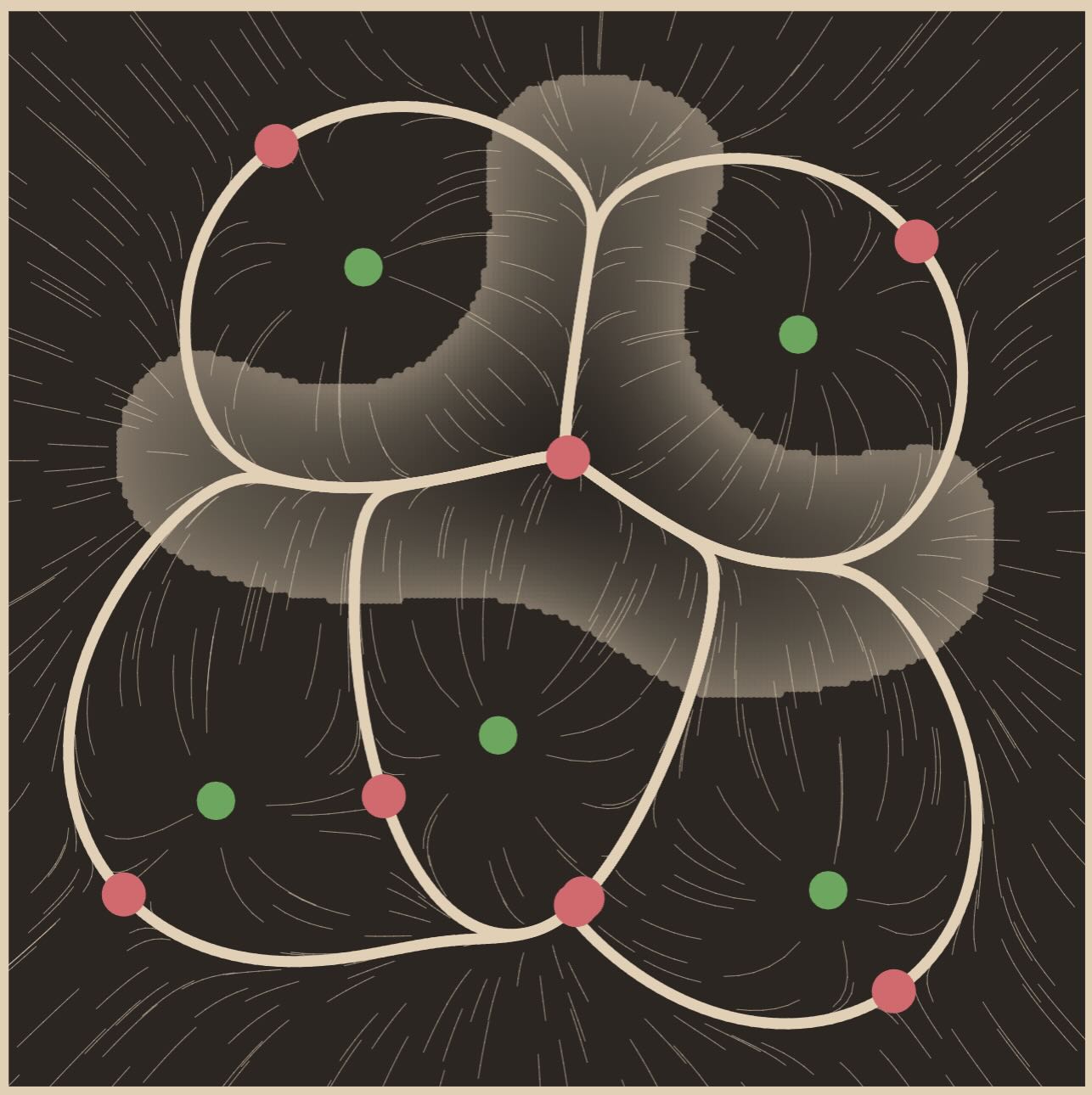
\[\int_\mathbb{C} \lvert f|^2 e^{-k \mid z \mid^2}<\infty\]The space of such functions is called the Segal-Bargmann space, which I discuss in more detail in The uncertainty principle on Segal-Bargmann space. Set $\Sigma=f^{-1}(0)$. Define $\rho: \mathbb{C} \backslash \Sigma \to \RR$ by $\rho(z) = \lvert f(z)\rvert ^2 e^{-k \lvert z\rvert^2}$. The morse theory of $\rho$ defines a decomposition of $\CC$. Indeed, each zero of $f$ is a local minimum of $\rho$. Let ${z_i}$ be the collection of zeros of $f$. We can define the “stable manifolds” of each $z_i$, the set of points which flow towards $z_i$ under the gradient flow of $\rho$. This is the “watershed” of the zero. Denote the stable manifold of $z_i$ by $D_i$, which is a 2-cell inside of $\CC$. The Biran decomposition in 2D states that when the $z_i$ are all distinct, each $D_i$ has area 1. Here is a visualization of the sets $D_i$ when $f(z) = \prod(z-z_i)$ is a polynomial:
Does not work on mobile! please play on desktop sorry
- The green points are the zeros of the polynomial $f(z) = \prod(z-z_i)$
- Click and drag to move the zeros
- Double click to add/remove zeros
- The slider controls the value of $k$
- The red points are the nonzero critical points of $\rho(z)$
- The thick white lines are the borders of the sets $D_i$, which we denote by the set $\Delta$
- The thin white lines are the gradient flow lines of $\rho(z)$
- The translucent white blob is the set where $\rho$ is large. Specifically, it is defined by
I prove that $S_\rho$ has area greater than $2\pi/k$ in The uncertainty principle on Segal-Bargmann space
The decomposition of $\CC$ into the blobs $D_i$ is known as the Brian decomposition. Each of the blobs has the same area! In particular, if $z_i$ is an isolated zero of $f$, then the stable manifold $D_i$ has area $\pi / 2k$.
We will attack this more generally. Consider a curve $\gamma$ which lies entirely in the boundary of $D_i$, meaning $\gamma:S^1 \to \Delta$. We will compute the area of enclosed in the curve. The result is
Theorem
For a simple curve $\gamma: S^1 \to \Delta$ enclosing a region $D$, the area of $D$ equals the number of zeros of $f$ contained in $D$ times $\frac{\pi}{k}$.
Applied to $\gamma = \del D_i$ the boundary of the stable manifold of an isolated zero $z_i$, the theorem implies $Area(D_i)=\frac{2\pi}{k}$ as desired. We can equally well handle multiple zeros. If $z_i$ is a zero of order $d$, then its stable manifold has area $\frac{2 \pi d}{k}$.
Let me describe the proof informally first. Our main trick is to compute the area enclosed by $\gamma$ using the Divergence theorem. Consider the log of the density,
\[l = \log(\rho) = \log|f|^2 - k \vert z \vert ^2\]Applying the divergence theorem around $\gamma = \del D$, we see that
\[\int_{\gamma} \hat{n} \cdot \nabla l = \int_{D} \nabla \cdot \nabla l\]Because $l$ is built from a holomorphic function, the right side is simple to compute. Away from the zeros of $f$, the first term of $l$ is
\[\log \vert f \vert^2 = \log f + \log \bar{f} = 2 \Re(\log(f))\]This is the real part of a holomorphic function. In particular, it is harmonic, so its laplacian vanishes. Therefore, away from zeros of $f$,
\[\nabla \cdot \nabla l = -k \nabla \cdot \nabla |z|^2 = -4k\]Unfortunately, $\log \vert f \vert^2$ is not everywhere defined. But, in a sense we will make precise later, $\nabla \cdot \nabla \log \vert f \vert^2 = \sum 4 \pi \delta_{z_i}$ for $z_i$ the zeros of $f$. The integral of this counts zeros of $f$. if $n$ denotes the number of zeros of $f$ contained in $D$, we expect
\[\begin{align}\int_{D} \nabla \cdot \nabla l \omega_0&= \int_D \left(- 4k + \sum 4 \pi \delta_i\right) \omega_0\\ &= 4 \pi n - 4 k \text{Area}(D) \end{align}\]To relate the number of zeros to the area, we need to choose a curve $\gamma$ where the other side of the divergence theorem $\int_{\gamma} \hat{n} \cdot \nabla l$ vanishes. That is, we need the normal vector to $\gamma$ to be perpendicular to $\nabla l$. In 2D, this is achieved by having $\gamma$ parallel to $\nabla l$, meaning $\gamma$ needs to consist of flowlines of $\nabla l$. But the flow lines of $\nabla l$ are exactly those of $\rho$! So, For $\gamma \in \Delta$, by the standard ethos of morse theory, it must lie in flow lines between saddle points and maxima of $\rho$. Therefore, the flux vanishes, and we get a relationship between area and contained zeros. Let me write this out more formally.
Proof of theorem
We want to show that the area enclosed by a simple closed curve $\gamma\subset \Delta$ containing $d$ zeros of $f$ is $2\pi d / k$. Since $\gamma$ is supported on $\Delta$, we know $\rho$ is nonzero, so $l=\log(\rho)$ is defined on $\gamma$. $\Delta$ consists of the stable manifolds of all nonzero critical points of $\rho$, hence the stable manifolds of every critical point of $l$ on $\CC \backslash \Delta$. Since $\dot{\gamma}$ is contained in the tangent space to $\Delta$, it must be parallel to $\nabla l$. Let $D$ denote the region enclosed by $\gamma$. the normal vector $\hat{n}$ of $\del D$ is perpendicular to $\dot{\gamma}$, and hence $\nabla l$. Therefore,
\[0 = \int_\gamma \hat{n} \cdot \nabla \rho = \int_\gamma \hat{n} \cdot (\nabla \log \vert f \vert^2) - k \nabla \vert z \vert ^2\]We compute the second term with the divergence theorem:
\[\begin{align} \int_\gamma \hat{n} \cdot -k \nabla \vert z \vert^2 \omega_0 &= -k \int_D \nabla \cdot \nabla \vert z \vert^2 \omega_0\\ &= -4k\int_D \omega _0 = -4 k \text{Area}(D) \end{align}\]We compute the first term using the Cauchy integral formula. We can reinterpret the integral $\int_\gamma \hat{n} \cdot \nabla \text{log} \vert f\vert^2 $ as a complex line integral. Paramertize the curve $\gamma$ as $\gamma(t)$. If we treat $\dot{\gamma}$ as a complex number, then $i \dot{\gamma}$ is proportional to $\hat{n}$, with length equal to $\vert \dot{\gamma}\vert$. Similarly, we can interpret $\nabla \text{log} \vert f\vert^2$ as a complex number:
\[\begin{align} \nabla \log \vert f \vert^2 &= \nabla (\log(f) + \log(\bar{f})) \\ &= \frac{\nabla f}{f} + \frac{\nabla \bar{f} }{f} \\ &= 2 \text{Re}( \frac{\nabla f}{f}) \end{align}\]All together, we can write the integral as a complex line integral
\[\begin{align} \int_\gamma \hat{n} \cdot \nabla \text{log} \vert f\vert^2 &= \int_{S^1} i\dot{\gamma} \cdot 2 \text{Im}( \frac{\nabla f}{f}) \de t\\ &= 2 \text{Re} \int_{S^1} i \dot{\gamma} \cdot \frac{\nabla f}{f} \de t\\ &= 2 \text{Re} \int_{S^1} i \dot{\gamma} \frac{f'}{f} \de t\\ &= 2 \text{Im} \oint_\gamma \frac{f'}{f} \\ &= 2 \text{Im} \oint_\gamma \de \log(f) \end{align}\]This measures (twice) the accumulated phase of $f$ along the path $\gamma$, or $2 \cdot 2 \pi d$ where $n$ is the winding number of the phase. $n$ equals the number of zeros contained inside $\gamma$. All together,
\[\begin{align} 0 &= \int_\gamma \hat{n} \cdot \nabla \text{log} |f|^2 - \int_\gamma \hat{n} \cdot \nabla -k|z|^2 \\ &= 4 \pi n - 4 k \text{Area}(D) \end{align}\]Rearranging, we have have proven our result:
\[\boxed{\text{Area}(D) = \frac{\pi n}{k}}\]Relation to usual Biran decomposition
I describe the Biran decomposition of a general Kahler manifold in my talk. The setup above is the specalization of the general story to the Kahler manifold $\CC$. Fix a symplectic form $\omega = k \omega_0$ where $\omega_0 = \de z \wedge \de \bar{z}$ is the standard area form. We choose a prequantum line bundle, a holomorphic line bundle $L \to \CC$ with a hermitian metric whose curvature is $\omega$. Since $\CC$ is contractible, this must be a trivial line bundle. The necessary hermitian metric is the gaussian $e^{-k \vert z \vert^2}$. A holomorphic section $f\in H^0(\CC,L)$ is simply a holomorphic function, with $L^2$ norm
\[\Vert f \Vert_L = \int_\CC \vert f \vert e^{-k \vert z \vert^2} \omega\]This is the geometric origin of the Segal-Bargmann space. We consider the log of the density function $’ = \log(\rho)$, which is defined away from the zeros of $f$. This is a plurisubharmonic function, meaning $\del \bar{\del} \rho = k \omega$. The critical points of $l$ are index 0 or 1, so the union of the its stable manifolds defines a 1-dimensional CW complex inside of $\CC$, which we denote by $\Delta$. This is the skeleton of the space $\CC - f\inv(0)$. The Brian decomposition suggests that $\CC \backslash \Delta$ is symplectomorphic to the symplectic disc bundle over $f\inv(0)$ of area $1/k$. Indeed, $\CC \backslash \Delta$ contains connected components consisting of the stable manifolds $D_i$, which we can think of as a disc bundles over ${z_i}$. Biran’s Decomposition theorem states that the fibers all have the same symplectic area $1/k$ relative to the symplectic form $\omega$. Relative to the standard form $\omega_0$, each fiber has area $1$. But the fibers are exactly $D_i$, so each $D_i$ has the same area.
Note that the Biran decomposition does not work perefectly, because $\CC \backslash \Delta$ has another component containing $\infty$, with infinite area. This is the cost of working on a noncompact manifold.
Sources:
Paul Biran 2001, LAGRANGIAN BARRIERS AND SYMPLECTIC EMBEDDINGS
- Original source for the Biran decomposition, and my main source this talk.
Olguta Buse, Richard Hind, 2011, Ellipsoid embeddings and symplectic packing stability
- Application of the Biran decomposition to symplectic embedding problems. They prove that any closed, integral kahler manifold has packing stability.
Emmanuel Giroux, 2017, Remarks on Donaldson’s symplectic submanifolds
- Proves the Biran decomposition for non-Kahler manifolds, using asymptotic holomorphic technique. Biran essentially did this in dimension 4 a while ago, but this works in any dimension.