Code Sketches
The Biran decomposition
Summary:
There is a clever way to split apart $\mathbb{C}$ into regions of equal area, using the morse theory of holomorphic functions. This is the first instantiation of a general procedure called the Biran decomposition. The symplectic structure of a Kahler manifold decomposes into two pieces: A symplectic disc bundle over a hyperplane section, and an isotropic skeleton. This Biran decomposition is a symplectic refinement of the Lefshetz hyperplane theorem. The proof uses the morse theory of the norm squared of a holomorphic section of the prequantum line bundle. We will use this to prove some lagrangian barrier phemonena. For example, every symplectic ball of radius $1/\sqrt{2}$ embedded in $\mathbb{C} \mathbb{P}^n$ interesects $\mathbb{R} \mathbb{P}^n$
Presented at:
- Student symplectic seminar
🔗 Link to file
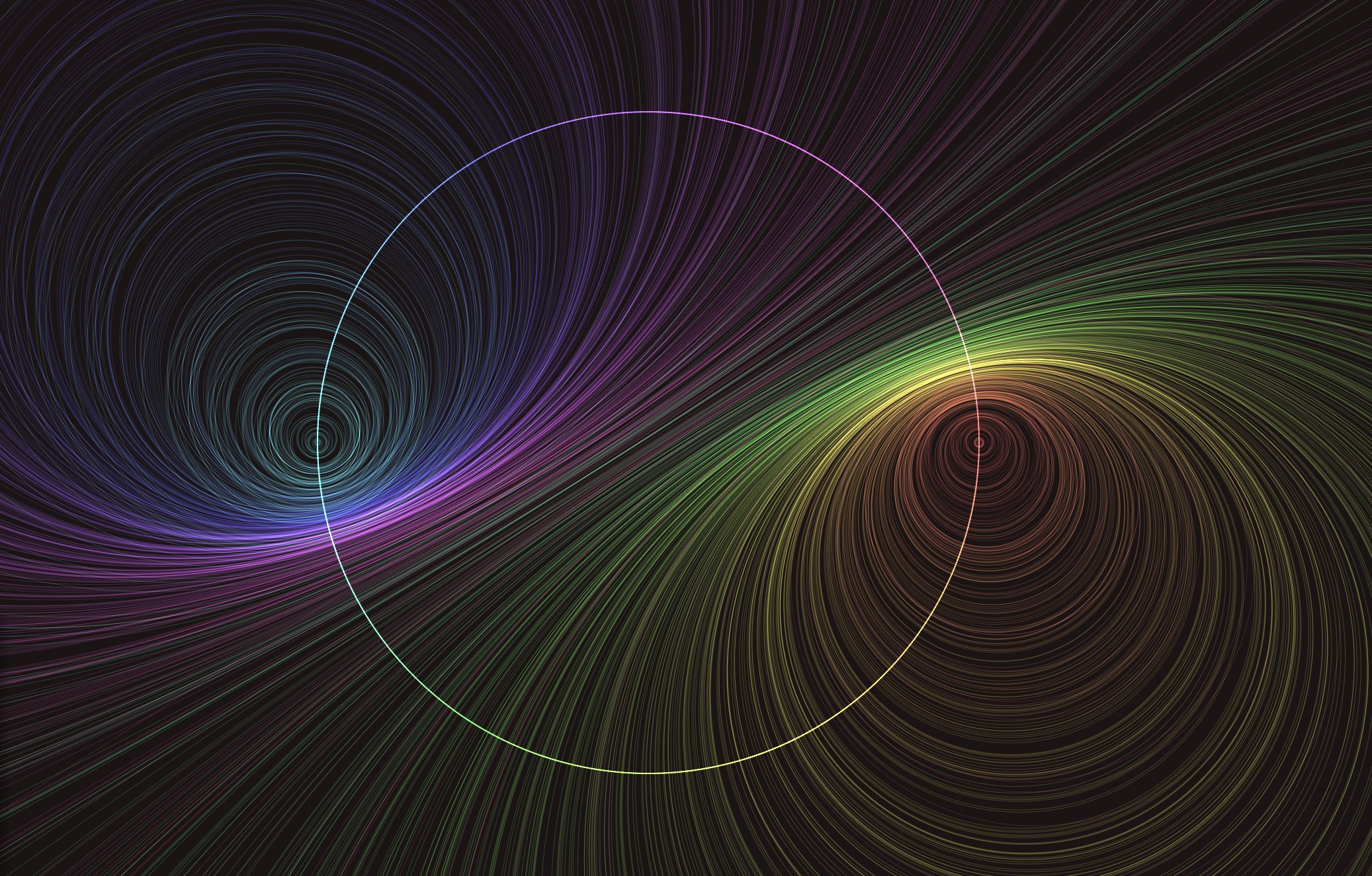
Hyperbolic string art
Summary:
I close my eyes, but all I see are strings. Stretch a line across a circle according to simple mathematical rules, and you get elegant patterns often dubbed “string art”. For example, connect each angle $\theta$ to the angle $2 \theta$, and the heart-shaped cardiod emerges. This talk chronicles my fourier into hyperbolic string art, a recontextualization of string art imagining the circle as the boundary of the hyperbolic plane, and the straight lines as hyperbolic geodesics. The patterns arising from natural hyperbolic transforms reveal the symmetries and geometry of hyperbolic space. With hyperbolic string art, we navigate the hyperbolic plane watching only the horizon, and visualize the moduli space of closed hyperbolic surfaces.
Presented at:
- UC Berkerly many cheerful facts, Fall 2023
🔗 Link to file
Link to sketch
Toric geometry and harmonic oscillators
Summary:
In Spring 2022, my final project for symplectic geometry class was a blog post on toric geometry, which incorperated processing sketches with math exposition. This, of course, blew way out of proportion. This is what I’ve started. First, I give a quick explination of symplectic geometry motivated by classical mechanics. Second, a description of toric manifolds through the lens of harmonic oscilators. In particular, I explain the Dual axis illusion as a consequence of toric geometry.
Link to sketch
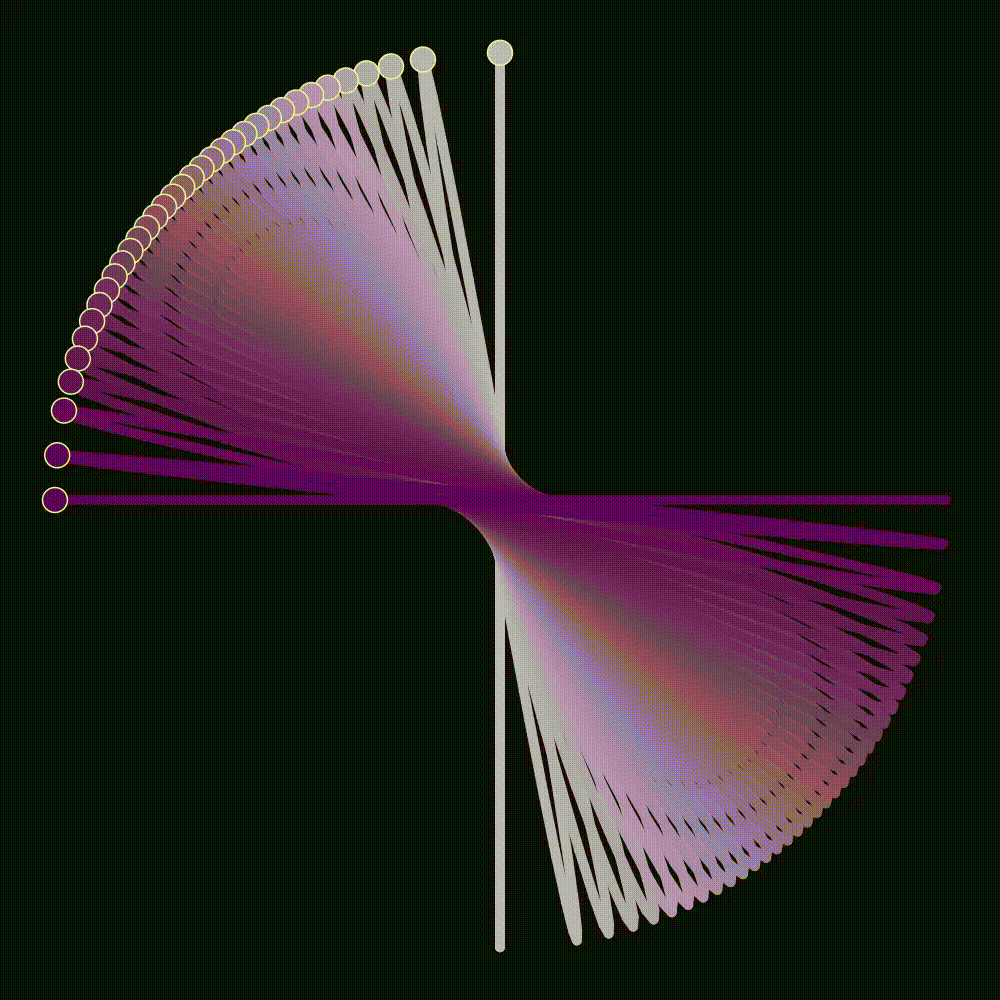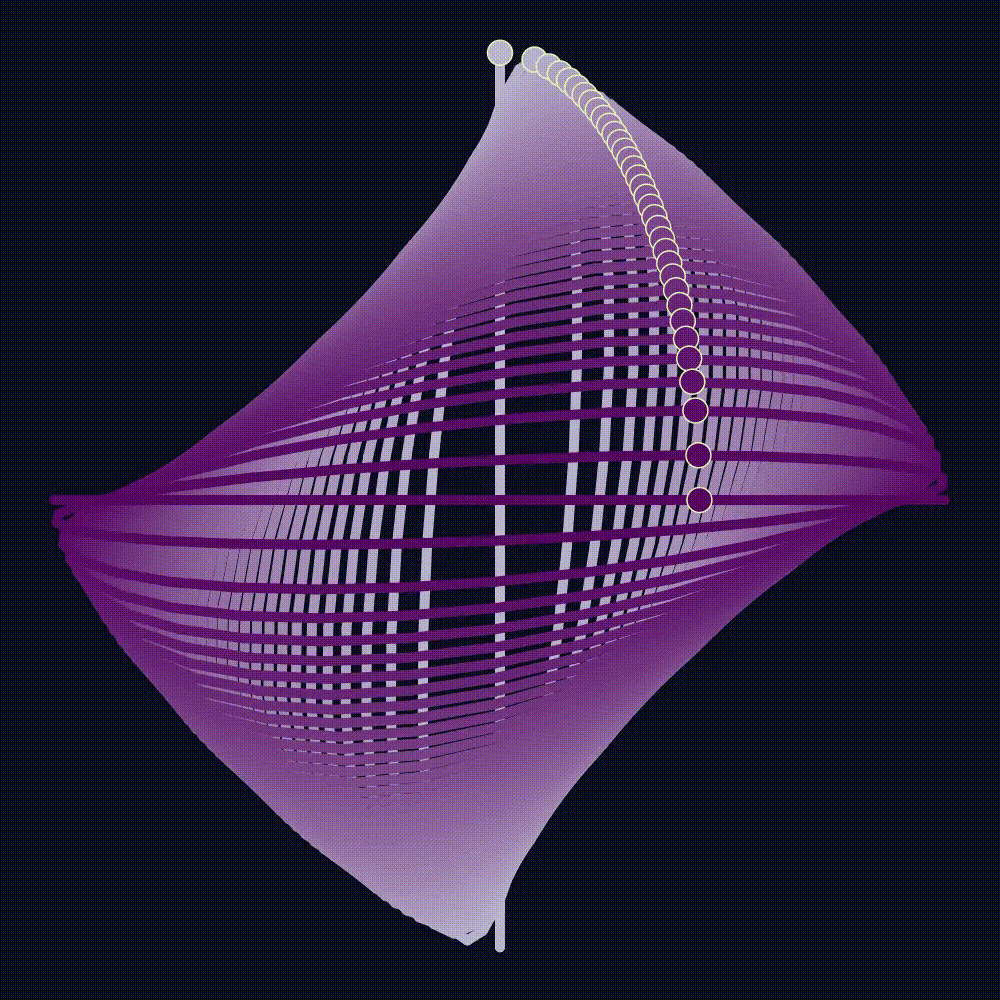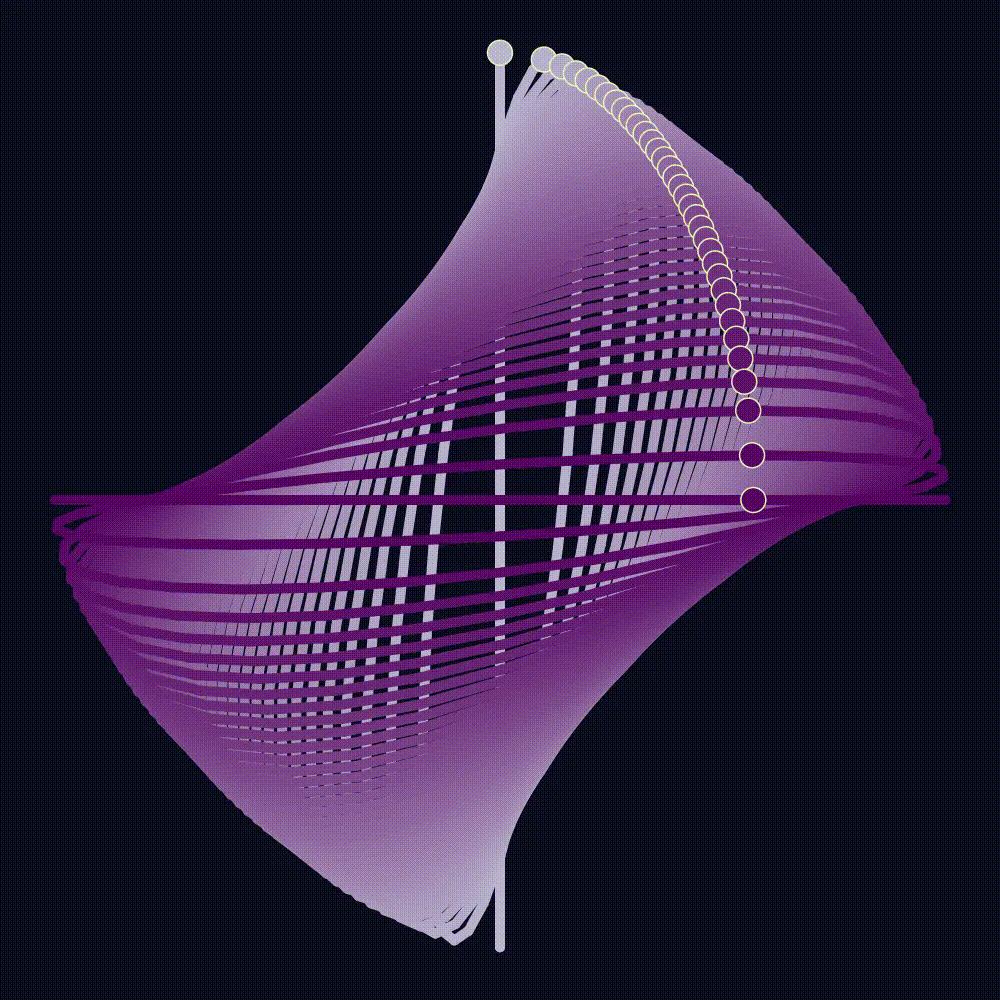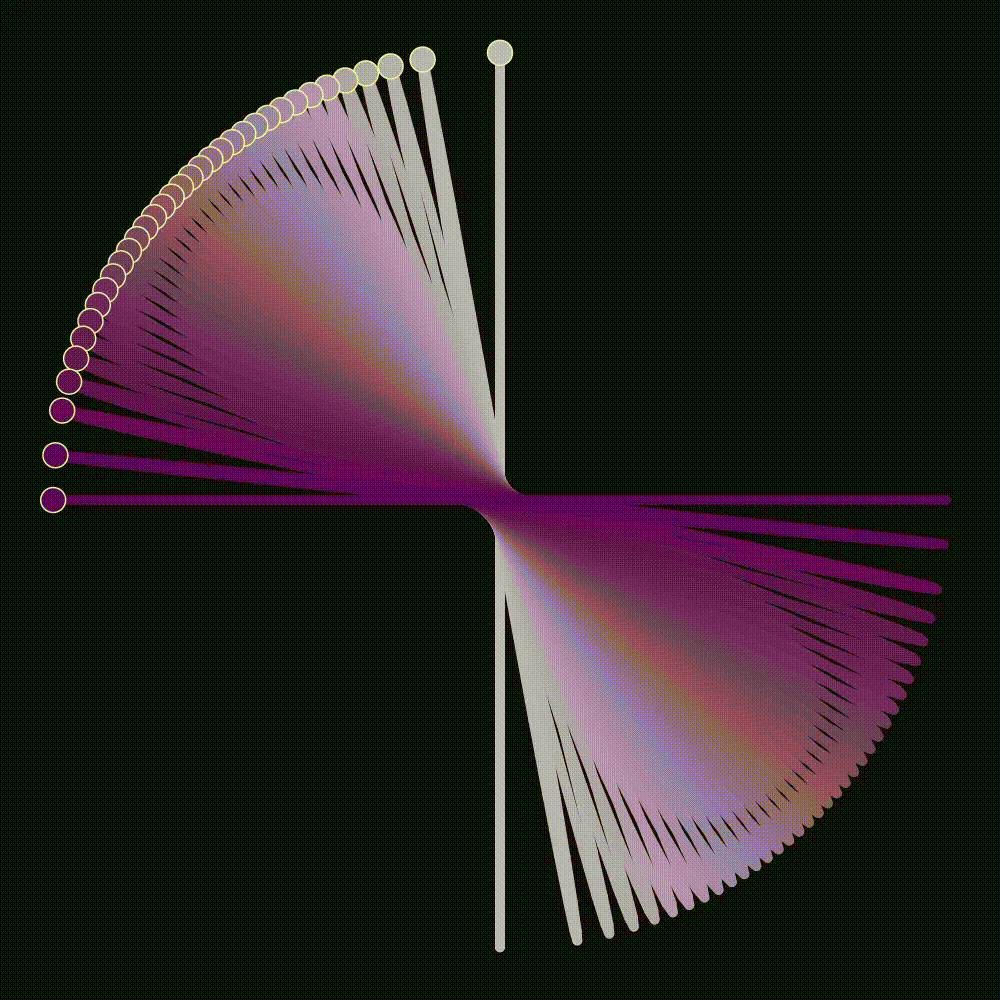
Dynamics of random maps
Summary:
An illustration of dynamics of a random map from the plane to itself. It plots the trajectories of a few random points, showing where and how they accumulate. The map is periodically modulating perlin noise. As the map changes, you can see all sorts of bifurcations and dynamic effects. Here are some more examples, and a little more context
Link to sketch
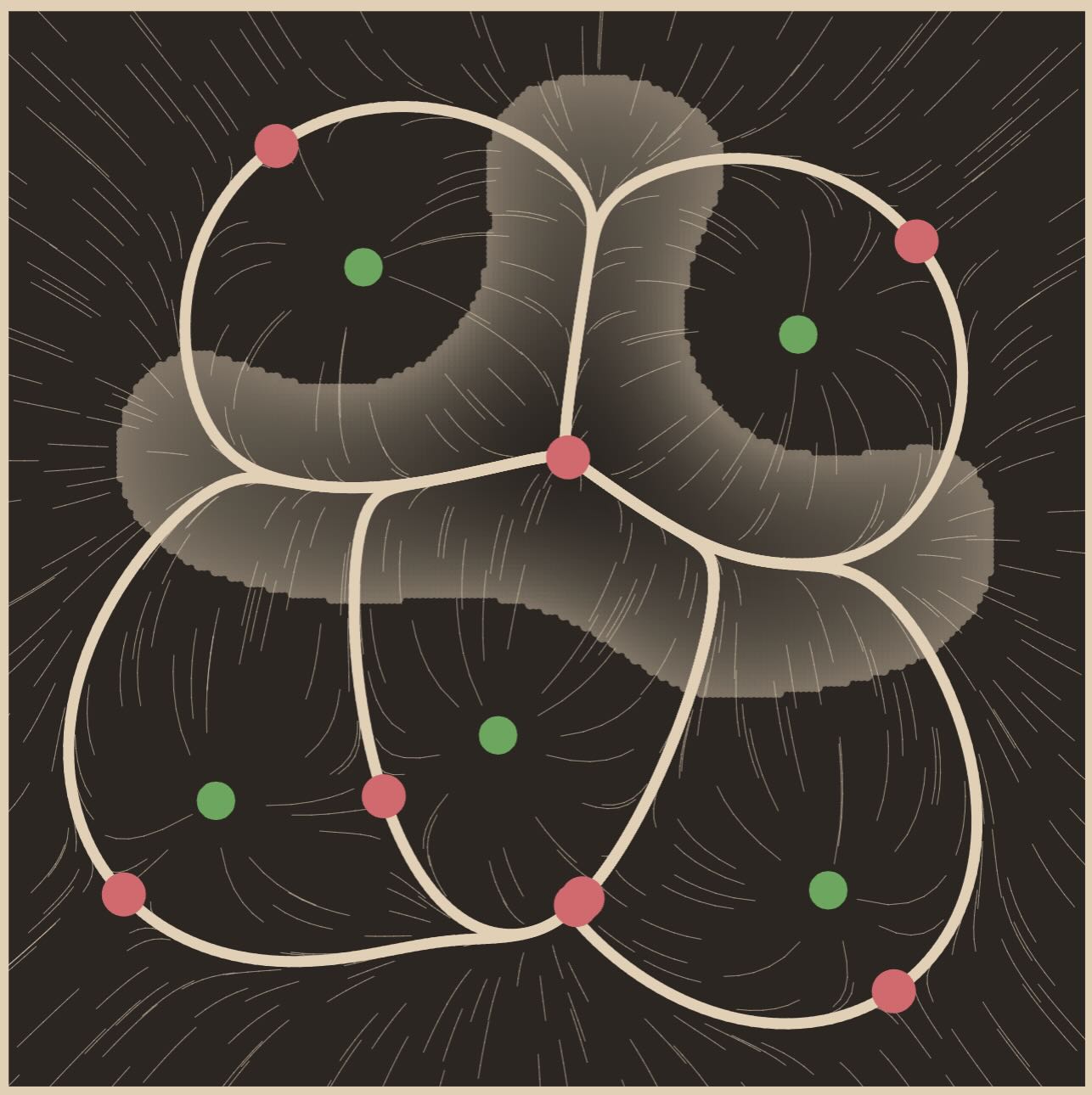
Hoops
Summary:
Just some fun little blobs, from when I first started to mess around with creative coding. I suggest looking thru the presets, some are pretty fun.
Link to sketch
(almost) Kam tori
Summary:
A failed attempt to find KAM tori, that still yeilded a neat result. Click the title for a brief description of what I was looking for (KAM tori), and what I got.