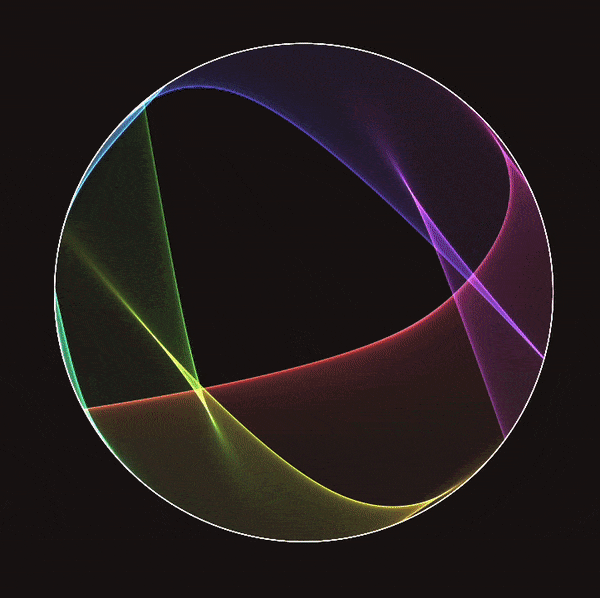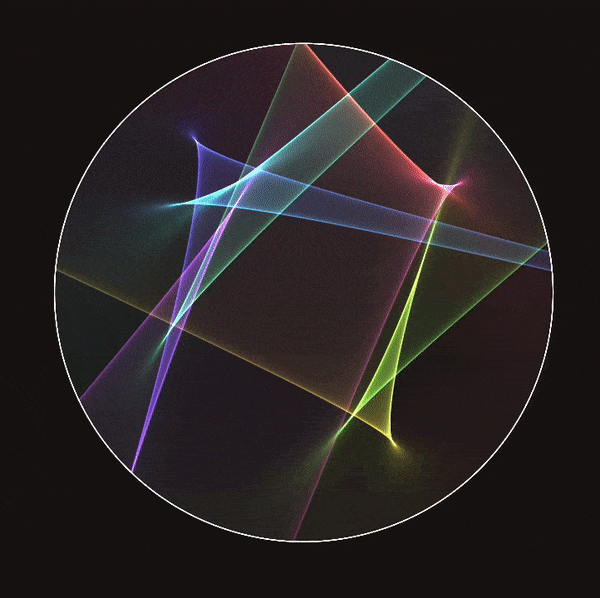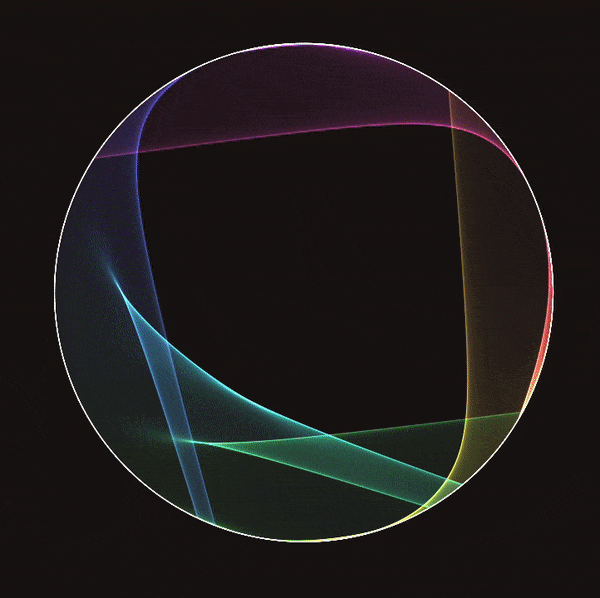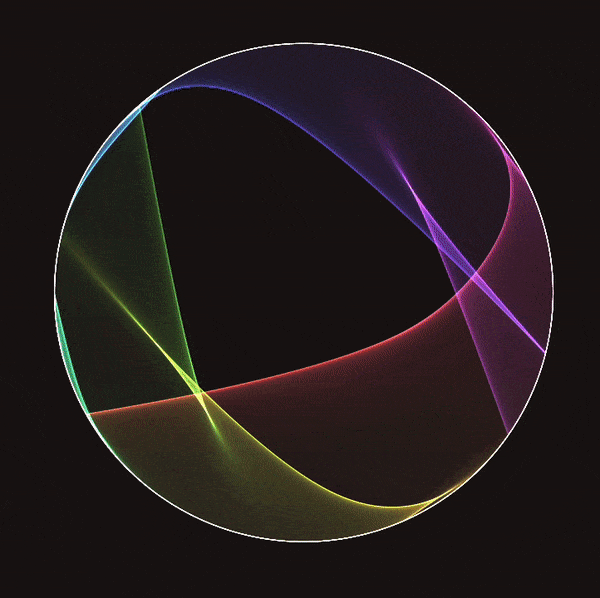Hyperbolic string art

Elliot Kienzle • Paper • 2022

blog talk code paper expository fun

Abstract:

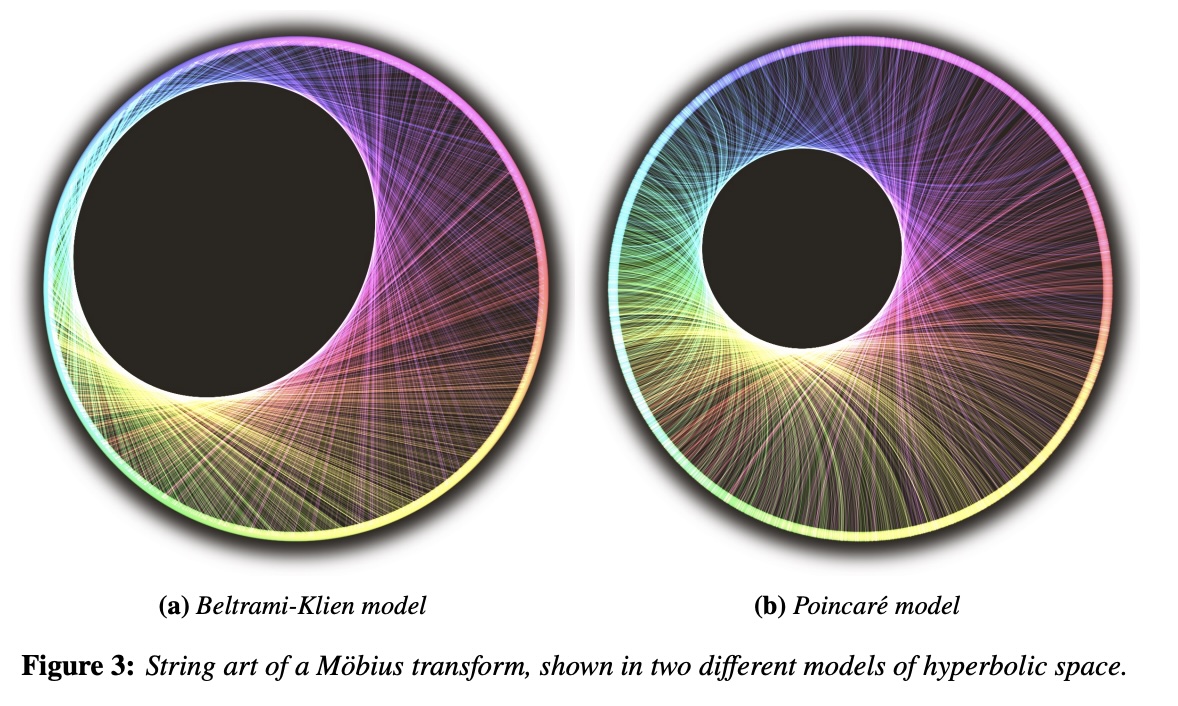
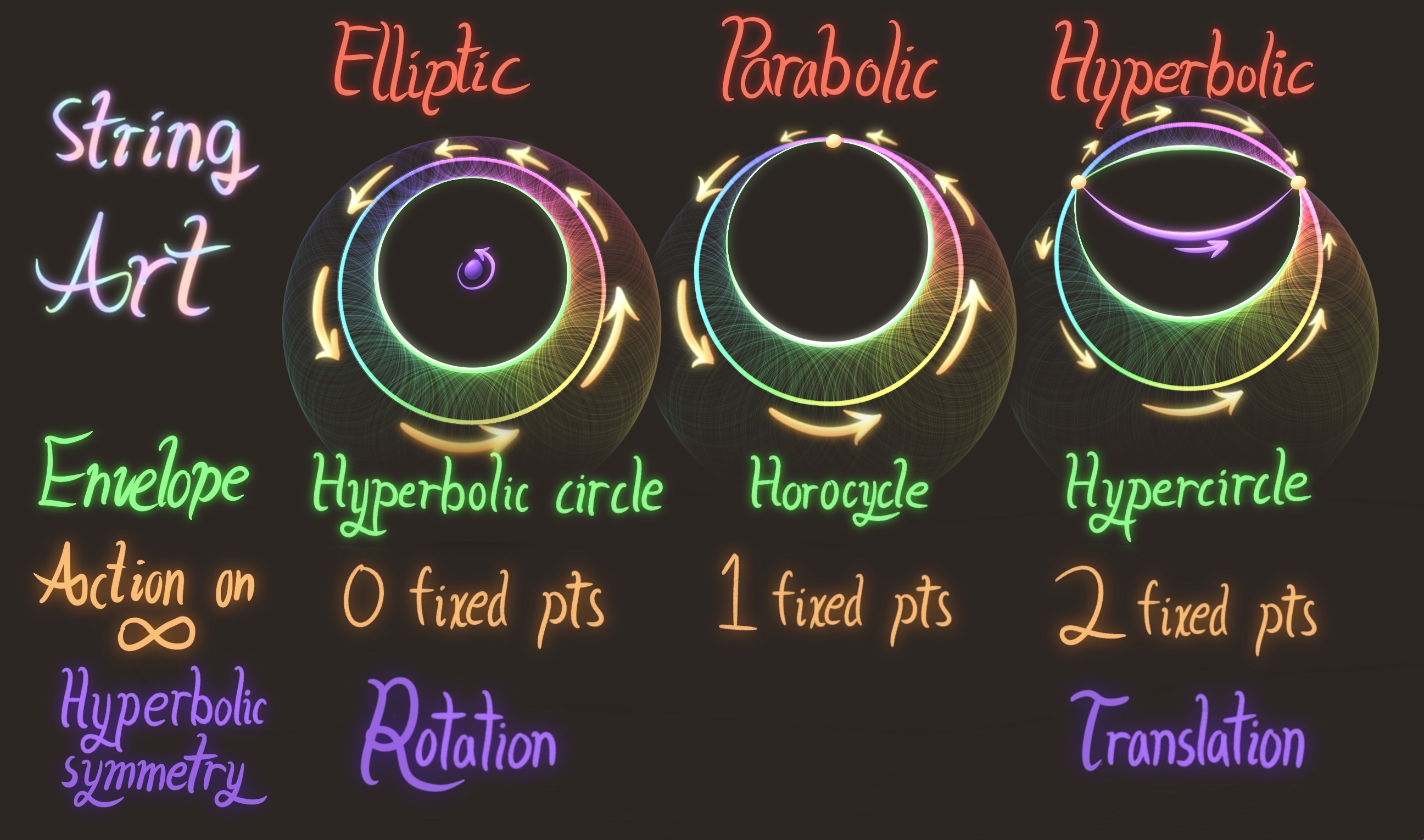
Stretching straight lines across a circle according to mathematical rules produces emergent patterns known as string art. We re-contextualize string art, envisioning the circle as the circle at infinity of the hyperbolic plane. The strings stretch across the Beltrami-Klein model of the hyperbolic plane, each line a hyperbolic geodesic. We examine the string art coming from Mobius transforms, by studying the envelope of the strings, the curve tangent to every string. We describe the envelopes of a Mobius transform in terms of the underlying hyperbolic symmetry. Elliptic Mobius transforms give hyperbolic circle envelopes, parabolic transforms give horocycles, and hyperbolic transforms give hypercircles. To visualize these envelopes, we use the Poincare disc model, rendering each string as a circular arc orthogonal to the boundary. This draws all envelopes described above as Euclidean circles. We conclude with a purely aesthetic application, showing a hyperbolic string art fractal

Presented at:

• UC Berkerly many cheerful facts, Fall 2023

Presentation file

Link to sketch

For a frielndly introduction to string art, see my twitter thread. This pge contians a collection of sketches of Hyperbolic string art. For a general audience introduciton to hyperbolic geometry and hyperbolic string art, see my paper. This paper was accepted to Bridges 2023, but I wasn’t able to make it that year. While reading the paper, try playing along with the sketches below. To play with string art in more granularity, see the full sketch.

Exploring hyperbolic space

This page contains a number of sketches exploring hyperbolic space. All of them are interactive, with the following controls:

Hyperbolic string art

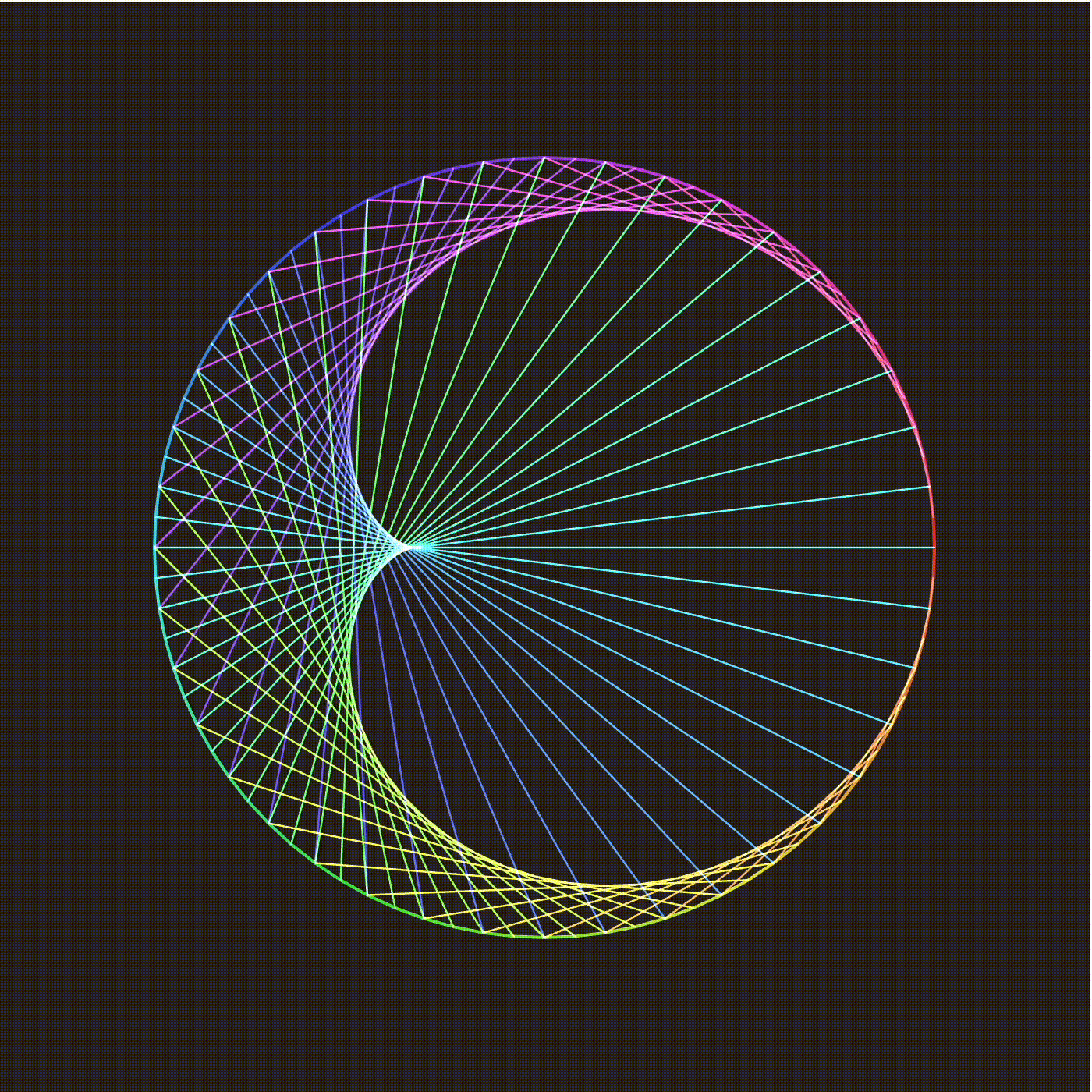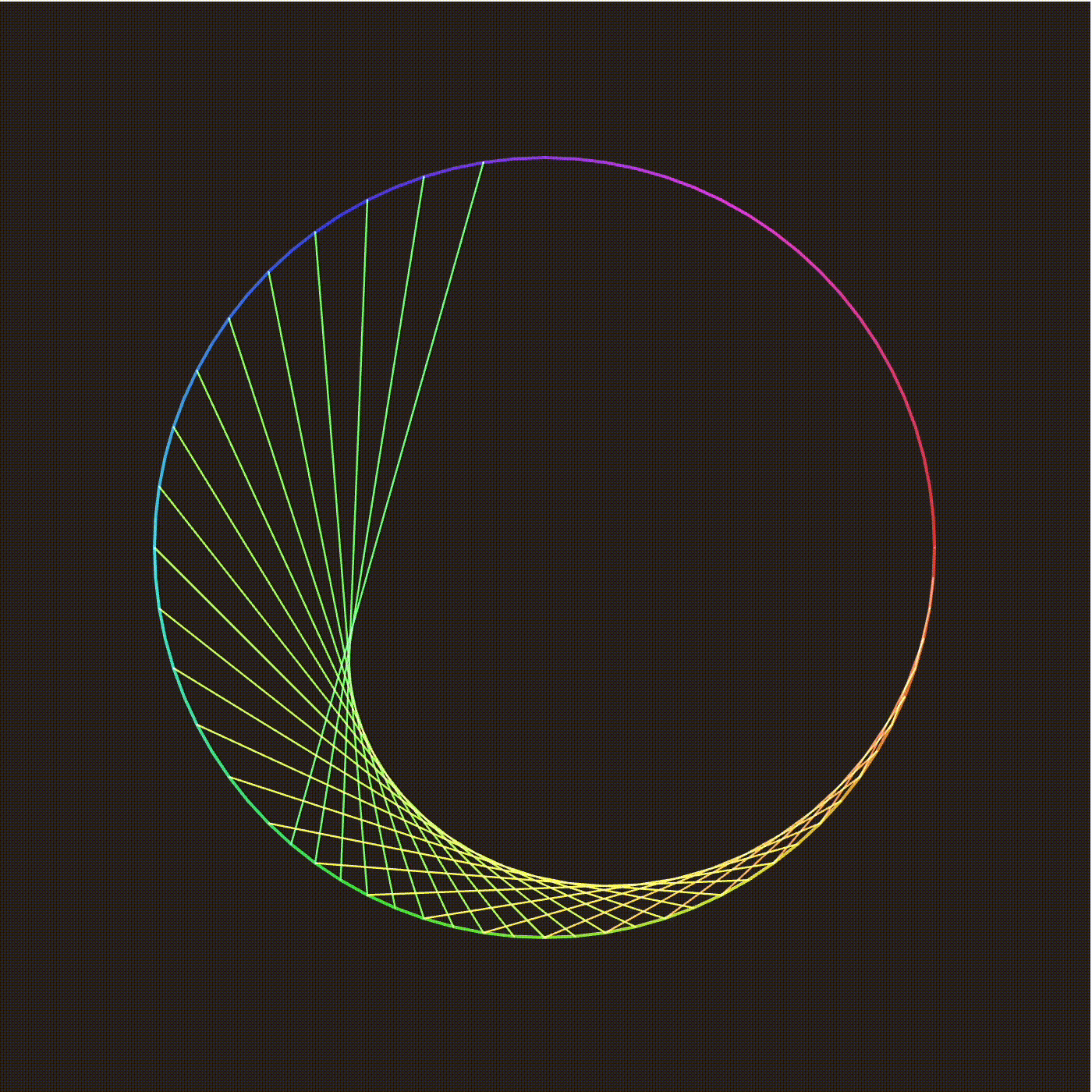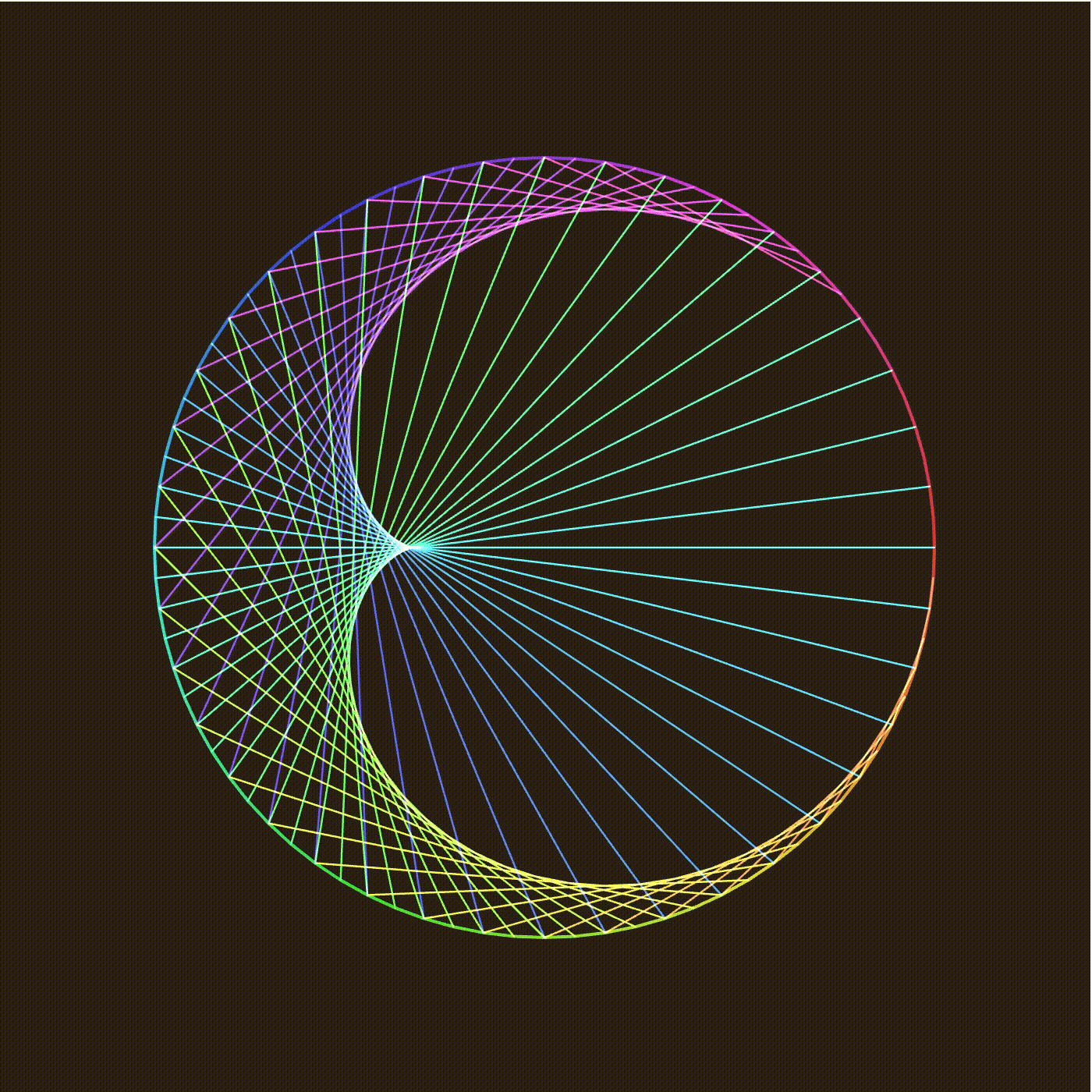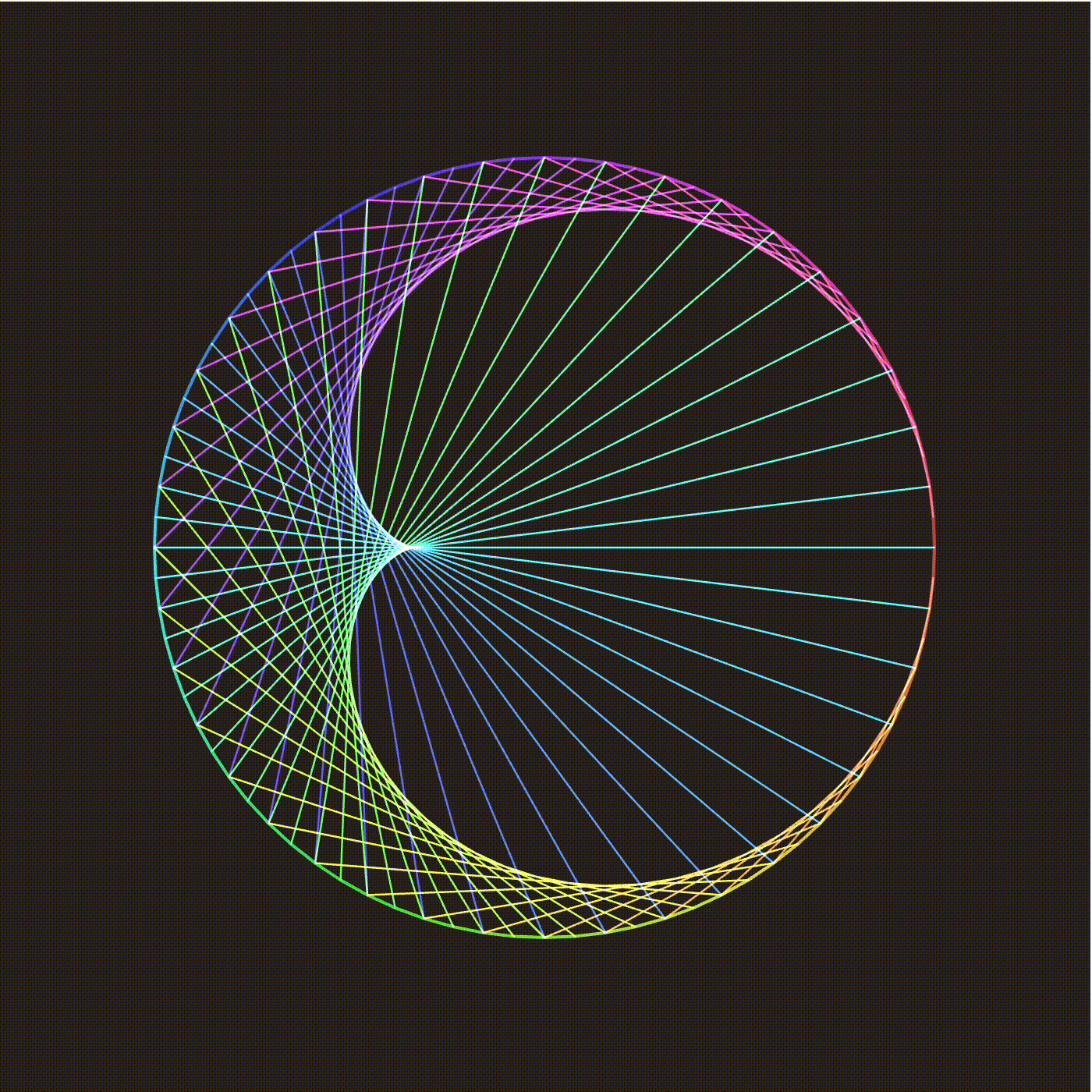
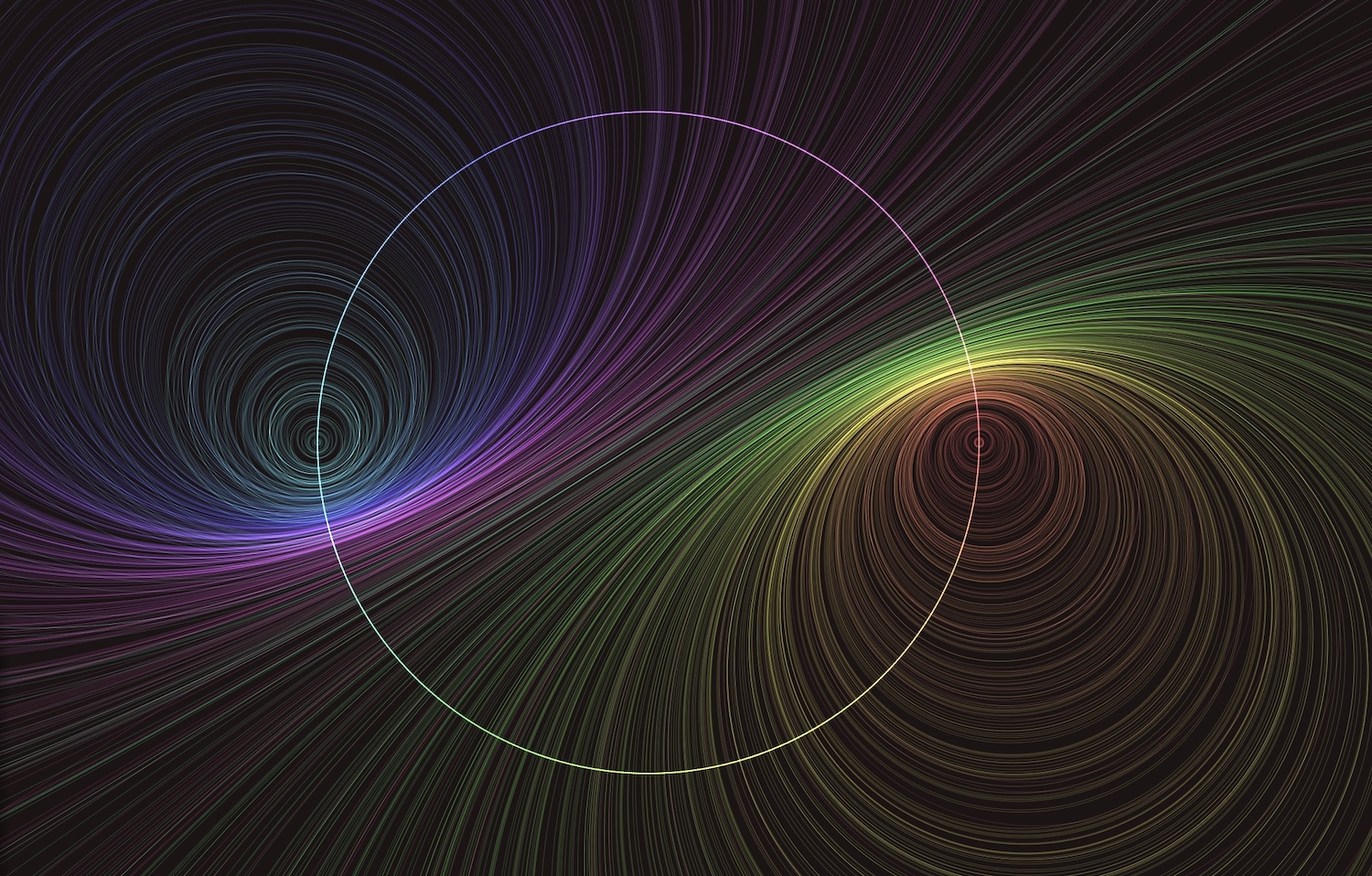
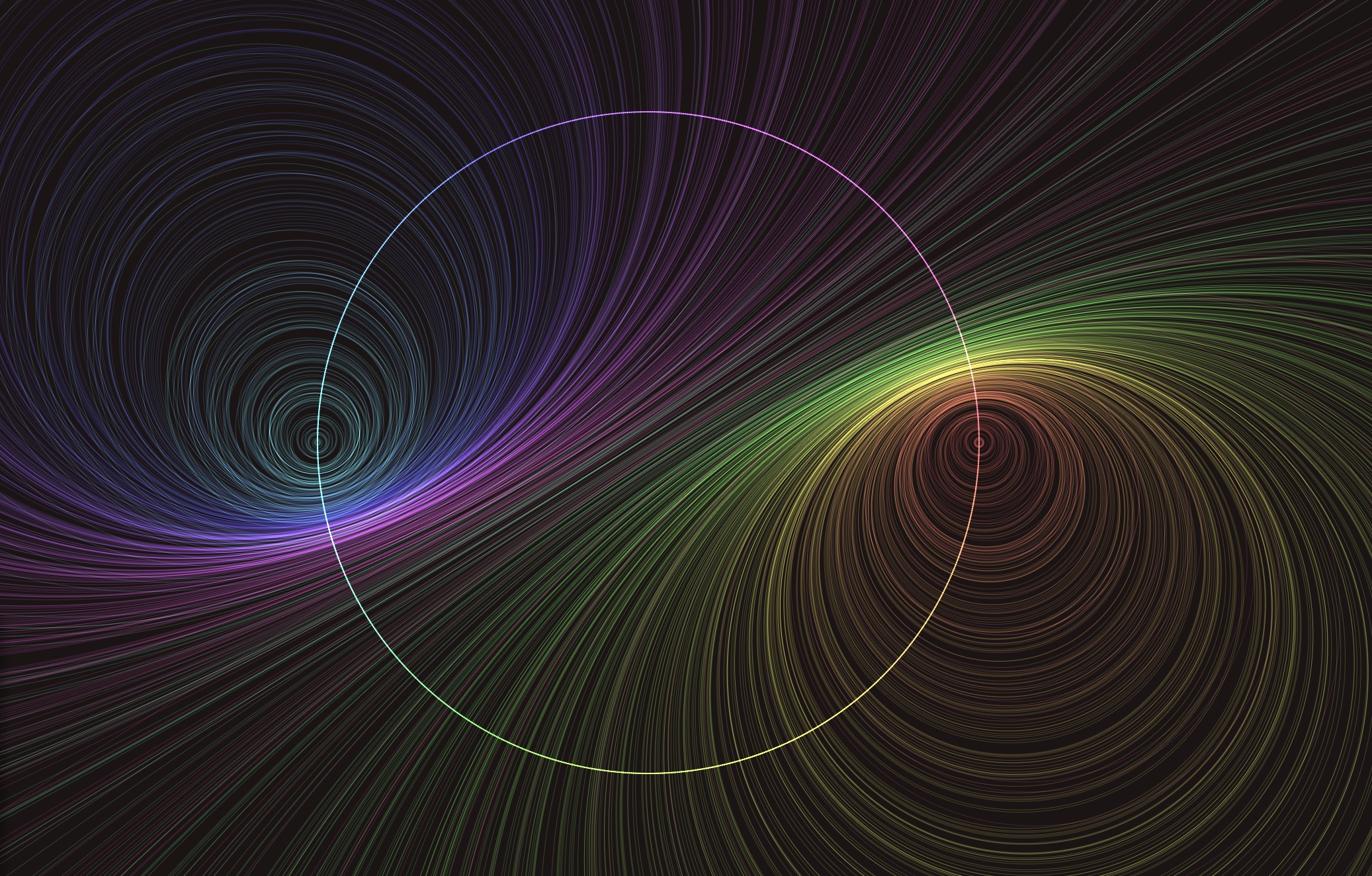
This shows a collection of hyperbolic geodesics (or strings), each connecting a point on the outside circle to a rigid rotation of that point. rotation angle controls this angle, and the number of strings controls the number of geodesics plotted. The white dot indicates the hyperbolic view. By holding the shift key, you can “fly around” the hyperbolic plane, seeing what the string art looks like from different perspectives. Notice that the strings concentrate around a circle. Let us see what happens with a hyperbolic Mobius transformation, coming from a translation in hyperbolic space:

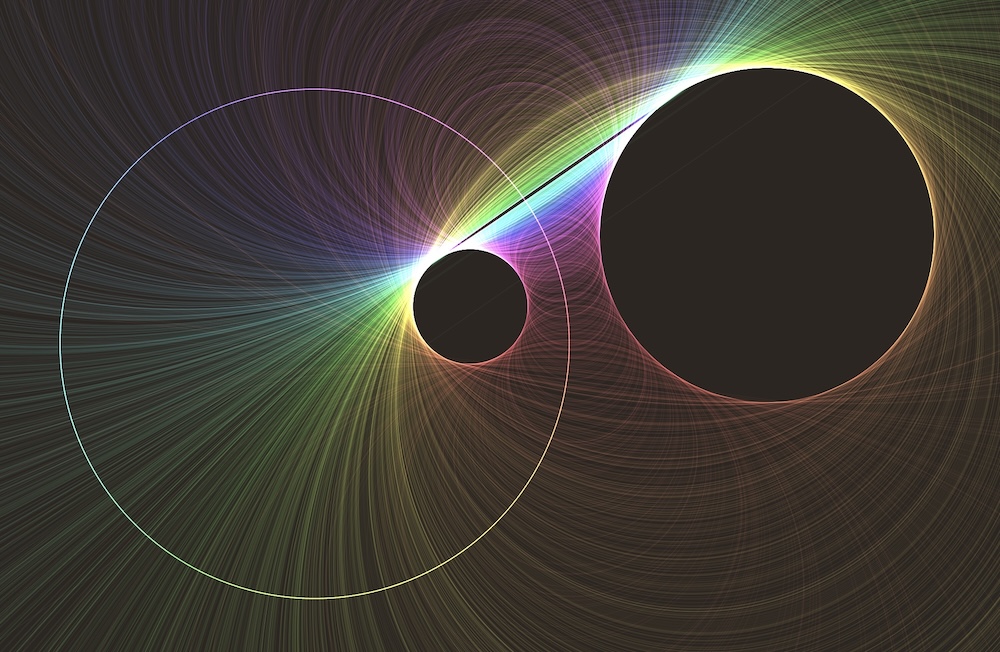
We are in a fixed view, but are changing the mobius transform controling the strings. The transform is a hyperbolic translation from the origin to the marked point. The strings now concentrate around arcs of Euclidean circles, known in hyperbolic space as Hypercircles.

I describe hyperbolic string art in more detail in an article. This gives a general audience quick introduction to hyperbolic geometry, and provides hyperbolic geometric descriptions for the envelopes seen above.

Farey tesselation

This lets you fly around the Farey tesselation. To form the Farey tesselation, identify the ideal boundary of hyperbolic space with the real line. Draw a geodesic between rational numbers $p/q$ and $p’/q’$ if and only if $pq’-p’q=\pm 1$. This relates to the action of $PSL(2,\mathbb{Z})$ via fractional linear transforms. In the Poincare disc projection, hese geodesics produce a tesselation of the hyperbolic plane by ideal triangles, equivariant under the Fuschian group $PSL(2,\mathbb{RR})$.

The Farey tesselation affords surprising connections between number theory and hyperbolic geometry. For example, take a geodesic from 0 to some real number. This geodesic passes a sequence of strings in the Farey tesselation, each associated with a rational number. These numbers form a sequence of best rational approximations of our original real number. In purely hyperbolic geometry, this tesselation uniformizes a once-punctured torus (combining two triangles, you get the desired ideal quadrilateral). For more details, see for example this paper.