Research Papers
Hyperbolic band theory through Higgs bundles
Elliot Kienzle, Steven Rayan • Published in Advances in Mathematics • 2022 • arXiv
Abstract:
Hyperbolic lattices underlie a new form of quantum matter with potential applications to quantum computing and simulation and which, to date, have been engineered artificially. A corresponding hyperbolic band theory has emerged, extending 2-dimensional Euclidean band theory in a natural way to higher-genus configuration spaces. Attempts to develop the hyperbolic analogue of Bloch’s theorem have revealed an intrinsic role for algebro-geometric moduli spaces, notably those of stable bundles on a curve. We expand this picture to include Higgs bundles, which enjoy natural interpretations in the context of band theory. First, their spectral data encodes a crystal lattice and momentum, providing a framework for symmetric hyperbolic crystals. Second, they act as a complex analogue of crystal momentum. As an application, we elicit a new perspective on Euclidean band theory. Finally, we speculate on potential interactions of hyperbolic band theory, facilitated by Higgs bundles, with other themes in mathematics and physics.
Expository Papers
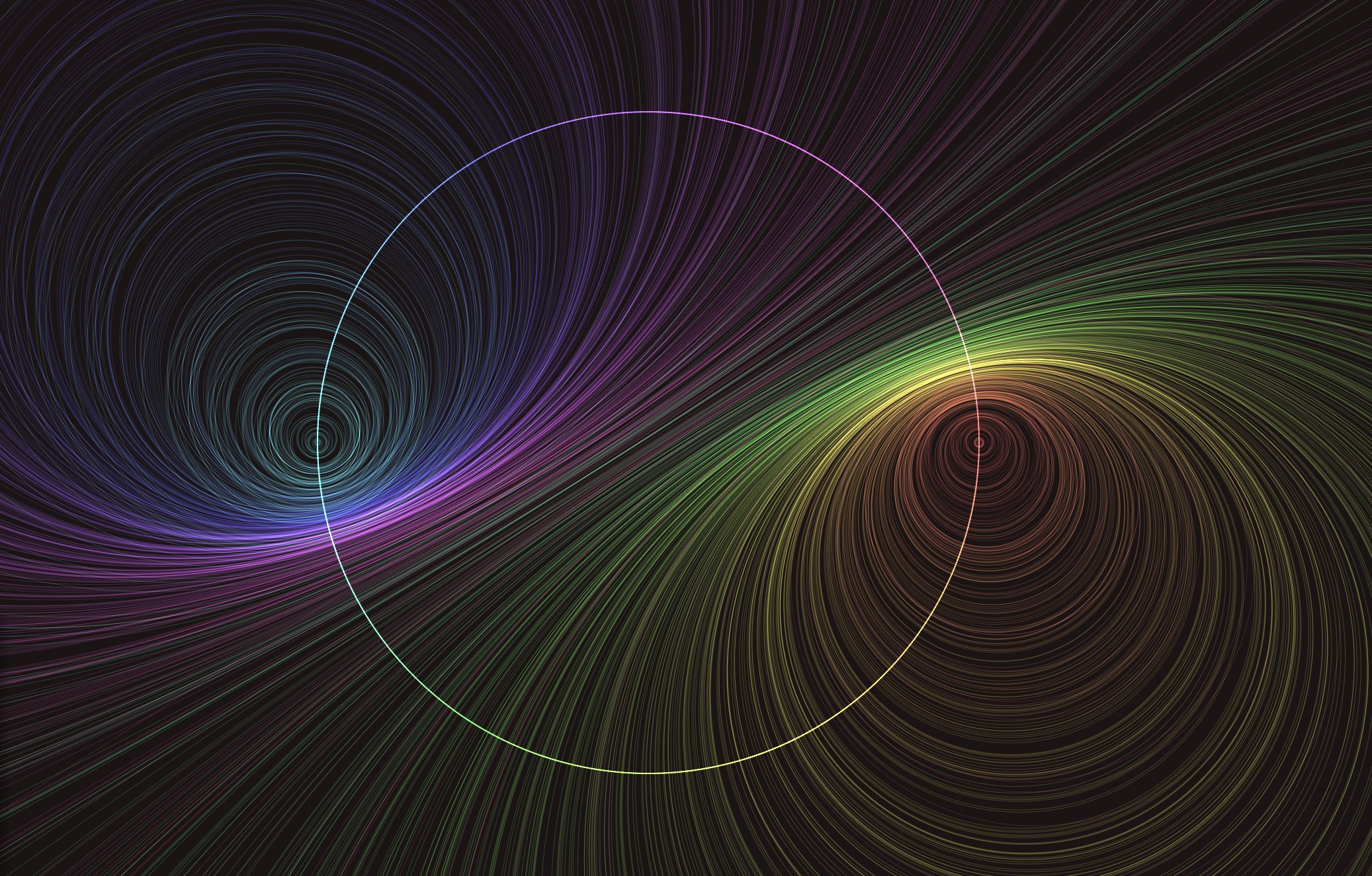
Hyperbolic String Art
Elliot Kienzle • Paper • 2022
Abstract:
Stretching straight lines across a circle according to mathematical rules produces emergent patterns known as string art. We re-contextualize string art, envisioning the circle as the circle at infinity of the hyperbolic plane. The strings stretch across the Beltrami-Klein model of the hyperbolic plane, each line a hyperbolic geodesic. We examine the string art coming from Mobius transforms, by studying the envelope of the strings, the curve tangent to every string. We describe the envelopes of a Mobius transform in terms of the underlying hyperbolic symmetry. Elliptic Mobius transforms give hyperbolic circle envelopes, parabolic transforms give horocycles, and hyperbolic transforms give hypercircles. To visualize these envelopes, we use the Poincare disc model, rendering each string as a circular arc orthogonal to the boundary. This draws all envelopes described above as Euclidean circles. We conclude with a purely aesthetic application, showing a hyperbolic string art fractal
Informal writing
- I write math threads on Twitter. Here are some old threads of mine.
- I sometimes upload things to my blog, which are generally less polished than my twitter threads.
- I’ve recently started a math diary, where I write about things I learn about that given day. This is entirely unpolished and unedited, but is perhaps of interest to someone.