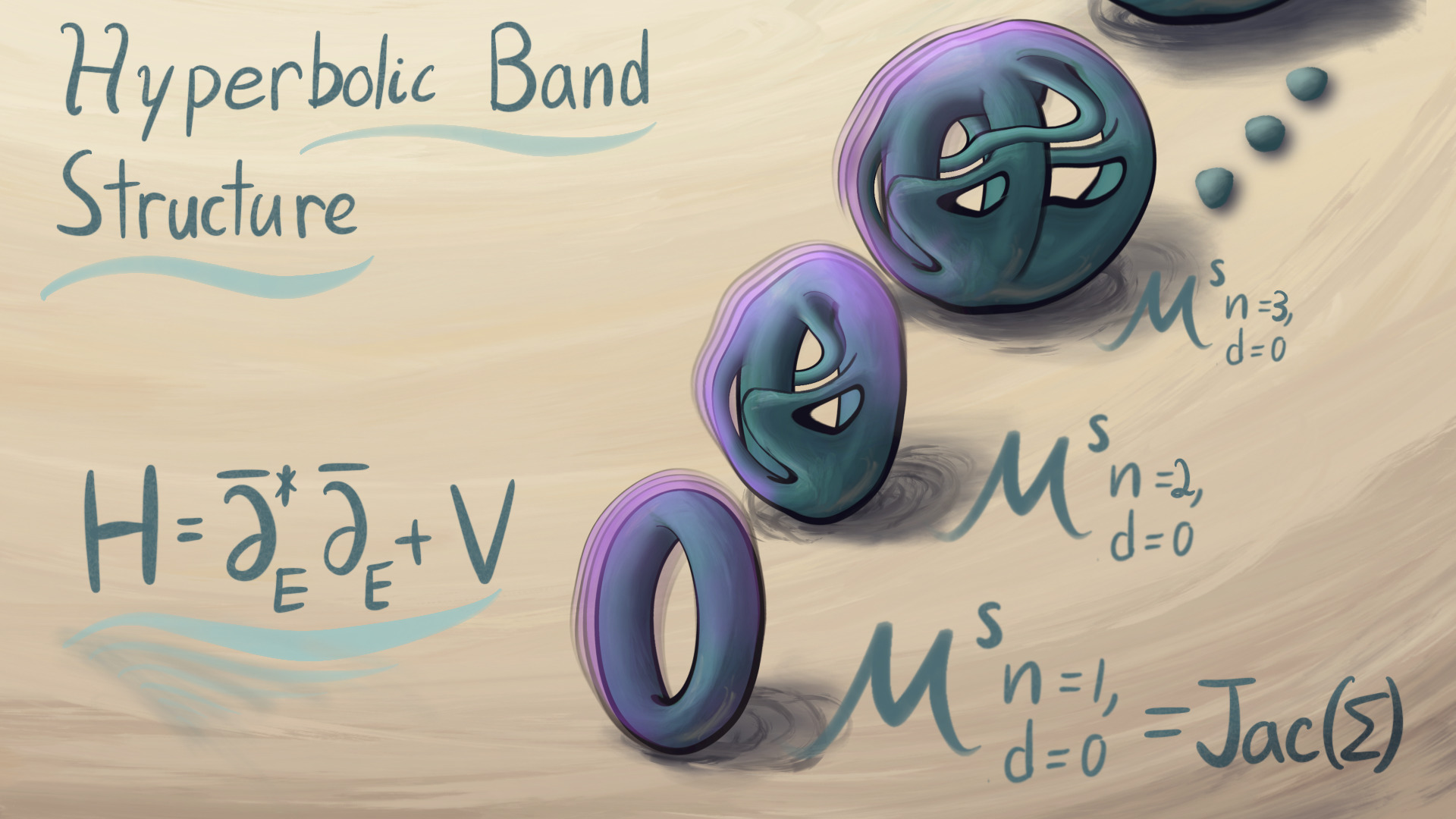Hyperbolic Band Theory Through Higgs Bundles
Elliot Kienzle, Steven Rayan • Published in Advances in Mathematics • 2022 • arXiv
Abstract:
Hyperbolic lattices underlie a new form of quantum matter with potential applications to quantum computing and simulation and which, to date, have been engineered artificially. A corresponding hyperbolic band theory has emerged, extending 2-dimensional Euclidean band theory in a natural way to higher-genus configuration spaces. Attempts to develop the hyperbolic analogue of Bloch’s theorem have revealed an intrinsic role for algebro-geometric moduli spaces, notably those of stable bundles on a curve. We expand this picture to include Higgs bundles, which enjoy natural interpretations in the context of band theory. First, their spectral data encodes a crystal lattice and momentum, providing a framework for symmetric hyperbolic crystals. Second, they act as a complex analogue of crystal momentum. As an application, we elicit a new perspective on Euclidean band theory. Finally, we speculate on potential interactions of hyperbolic band theory, facilitated by Higgs bundles, with other themes in mathematics and physics.
Presented at:
- Geometry and Mathematical Physics Seminar at the University of Saskatchewan
- JMM 2022 AMS Contributed Paper Session
- MSRI gauge theory graduate student seminar
Presentation file
For a gentle introduction to this project, see my Twitter threads: part 1 and part 2
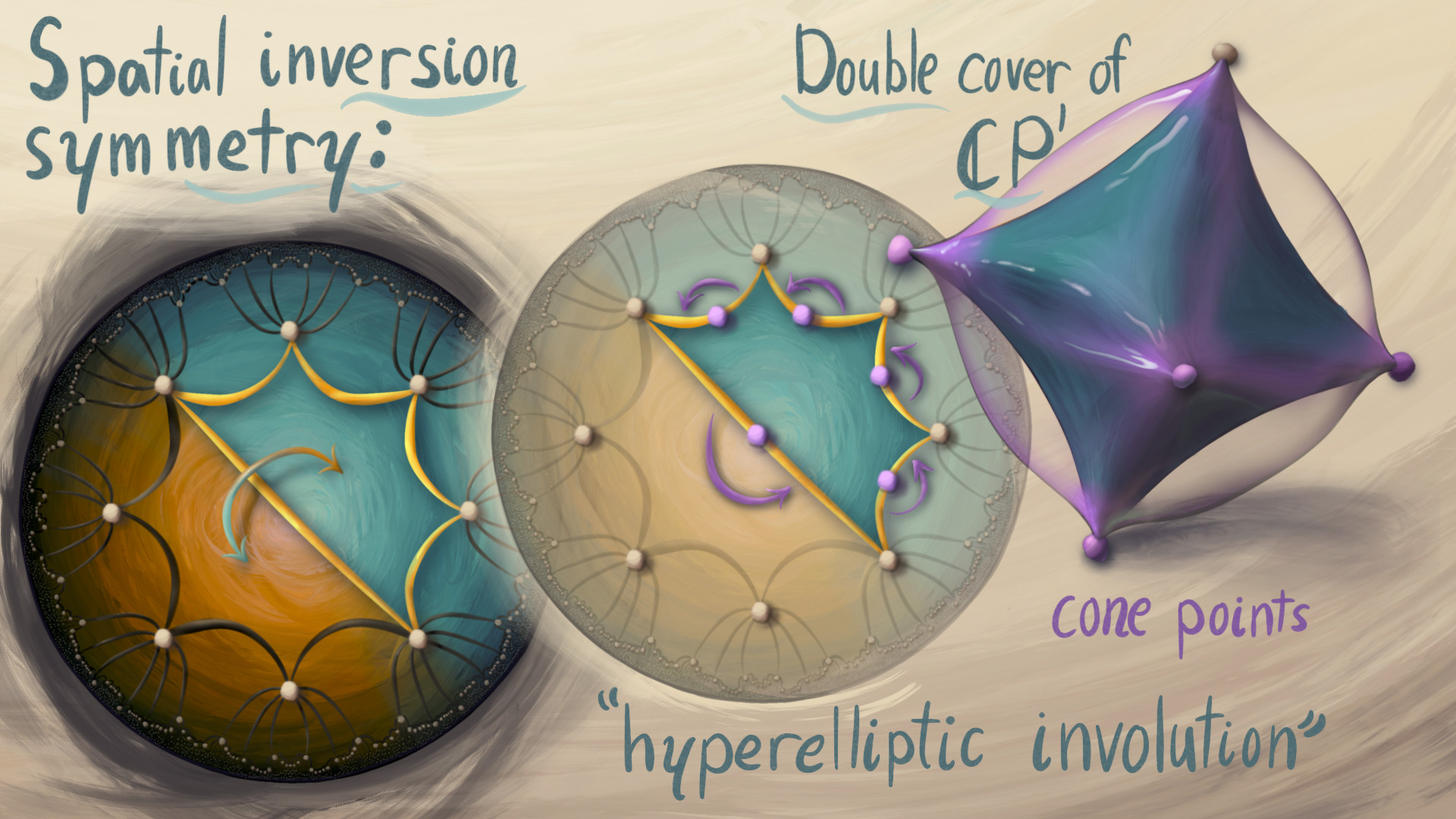
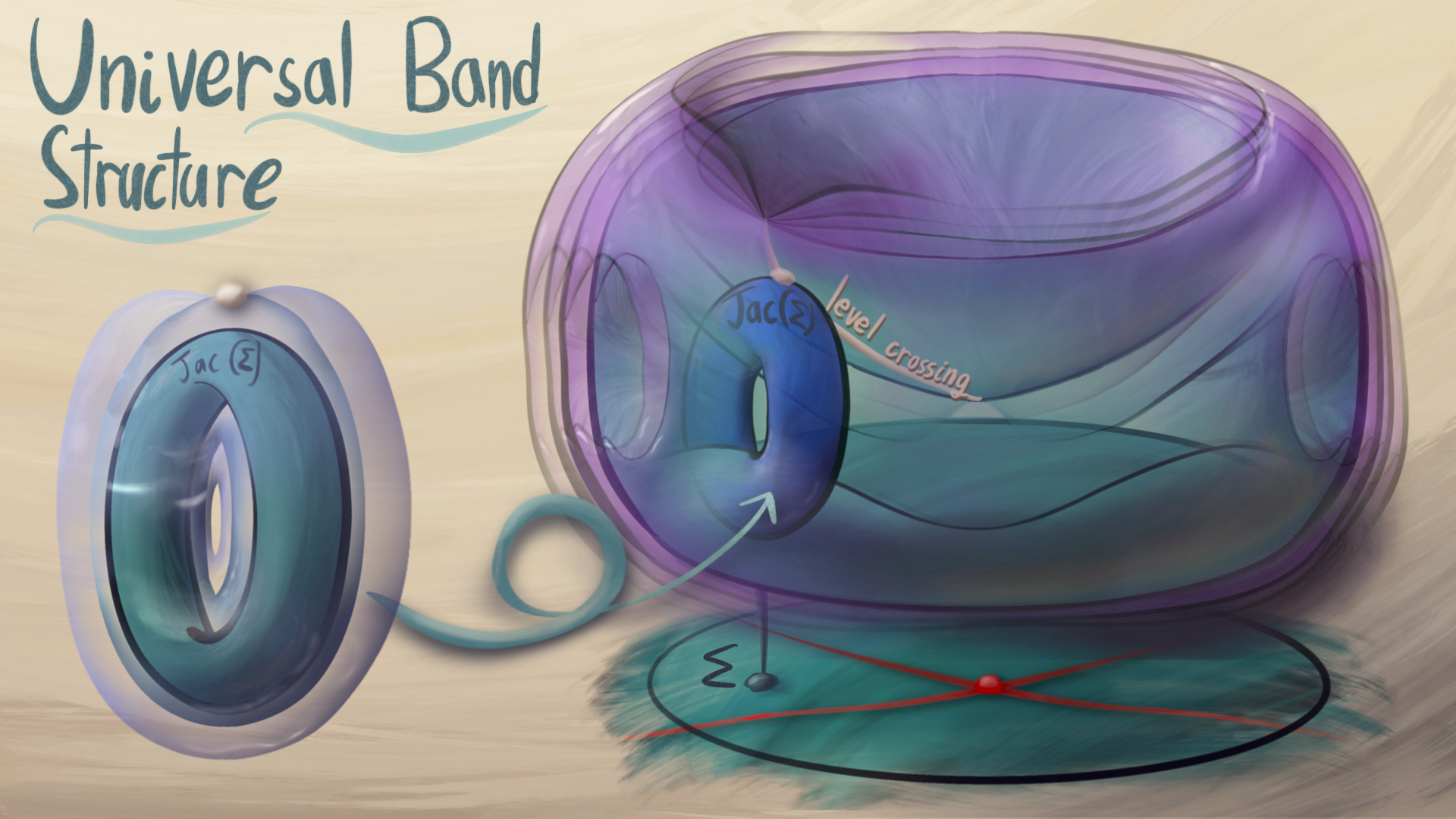
This project explores a bridge between algebraic geometry and condensed matter physics. On the physics end, we consider the quantum physics of hyperbolic crystals. Imagine an electron on a two-dimensional hyperbolic plane, evolving under a potential that is periodic under a set of hyperbolic translations. For example, Fig. 1 shows a regular hyperbolic crystal. The quantum properties come from the spectral theory of an associated periodic Schrodinger operator. We can understand the spectrum much better if we split it according to representations of the symmetries, a technique called hyperbolic band theory.
 |
|---|
| Fig 1: A regular tiling of a hyperbolic plane. Hyperbolic translations move one crystal cell to another, indicated by the red and yellow arrows. |
In algebraic geometry land, representations of the crystal symmetries become vector bundles on Riemann surfaces (See Hyperbolic band theory). In this project, we extend this theory to Higgs bundles, a complexified analog of Higgs bundles. We find two independent crystalographic interpretations of Higgs bundles, one from the algebro-geometric side of Higgs bundles, and the other from the representation-theoretic side.