Toric geometry and harmonic oscillators
Summary:
In Spring 2022, my final project for symplectic geometry class was a blog post on toric geometry, which incorperated processing sketches with math exposition. This, of course, blew way out of proportion. This is what I’ve started. First, I give a quick explination of symplectic geometry motivated by classical mechanics. Second, a description of toric manifolds through the lens of harmonic oscilators. In particular, I explain the Dual axis illusion as a consequence of toric geometry.
Link to sketch
Page still under construction, please excuse the typos
Introduction
A physicist sees the world through harmonic oscillators. The very first thing they study is the motion of a spring, equivalently a particle sitting in a characteristic quadratic potential. They then generalize to quantum mechanics, or to classical field theory and the wave equations, then to the free field in quantum field theory. Reality is merely a perturbed oscillator. Armed with this simple example they completely understand, physicists can tackle much harder problems.
What then is the geometer’s harmonic oscillator? It’s not so cut and dry, but I’d argue its the circle. The group of circle rotations $U(1)$ is one of the simplest Lie groups, being 1 dimensional and thus abelian. Unlike it’s cousin \(\mathbb{R}\), \(U(1)\) is compact and has a little bit more meat on its bones. Moving to geometry, you can “rotate” a manifold with a \(U(1)\) action, imposing useful symmetries. Taken to its logical extreme, a “toric” manifold has a maximal possible set of independent rotations, encoded by an action by the torus group \(U(1)^n\). These manifolds are entirely determined by their rotation structure, which is moreover entirely combinatorial. This is neatly encoded in a polytope, from which you can read off nearly every property you could care about. Toric manifolds are a geometers playground, letting them easily test their ideas. Like the oscillator, it is a simple example which we completely understand. 1
The analogous role of toric manifolds and harmonic oscillators is no accident. In the framework of symplectic geometry, a field born form classical mechanics, many circle actions come from harmonic oscillators. I want to show you toric geometry through a physicists glasses, promoting harmonic oscillators to a starring role. As we will see, they give concrete dynamical interpretations to all the big ideas
The shape of motion: A primer on geometric mechanics
The Hamiltonian formulation of classical mechanics studies motion of objects, like a ball on a spring, as a flow through some phase space. Like most physics, phase space was originally implicitly assumed to be Euclidean, but the complexities of celestial mechanics outgrew this local version. Phase space was reinterpreted as a manifold, endowed with a “symplectic form” which controlled the dynamics. Thus, symplectic geometry was born. Eventually, symplectic geometry separated from its physical origin to become its own field of mathematics.
We start with the canonical example, which we will develop much, much more over time
The harmonic oscillator and Hamiltonian mechanics
Consider a ball on a spring. This gives a restoring force proportional to its displacement, which is lots of fun to throw around. You can grab it with your mouse:
The force is proportional to the acceleration, meaning the motion is described by the following differential equation:
\[\ddot{x} = -x\]Where all annoying constants like mass or the spring constant are set to one. The dynamics of this diffeq are easier to grasp in its equivlent system of first order of coupled differential equations:
\[\dot p = - x\] \[\dot x = p\]a physical state is a pair of position \(x\) and “momentum” \(p\), defining a point in “phase space” \(\mathcal{P} =\mathbb{R}^2\).
The equations are encoded in a vector field over phase space. Solving the system, a state evolves by rotating at a constant rate in \(\mathbb{R}^2\). Focusing on the position, we see the particle oscillates sinusoidally with time.
We can cast theses equations in the more suggestive form
\begin{gather}
\dot p = -\frac{\partial H}{\partial x} \qquad \dot x = \frac{\partial H}{\partial p}
H(x,p) = p^{2} + x^{2}
\end{gather}
==say why these come from: Rotate 90 degrees==
The evolution of position and momentum are controlled by the derivatives of a single function on phase space, which we call the Hamiltonian.
The harmonic oscillator is characterized by the quadratic Hamiltonian. Their physical ubiquity stems from the mathematical role of quadratics, appearing as low order terms in Taylor series. But this Hamiltonian has a distinguished property that we’ve already seen: It generates rotation! If you start with a set of points set at different distances from zero, they will rotate at lock step, never falling out of phase. Formally, we can represent the evolution of a point of phase space \(\mathcal{P}\) after time \(t\) by a map \(\psi_t : \mathcal{P} \to \mathcal{P}\). The harmonic oscillator is periodic with period \(T = 2\pi\), meaning everything returns after time \(T\), \(\psi_T = id\). This periodicity, along with the identity \(\psi_t \circ \psi_s = \psi_{t+s}\), means the evolution \(\psi_t\) is an \(U(1)\) action on \(\mathcal{P}\). This is the fundamental connection between harmonic oscillators and the circle group, mentioned in the introduction. We will see many consequences of this connection below.
Remark
The harmonic oscillator is uniquely characterized by this periodicity. There are many other Hamiltonians on \(\mathbb{R}^2\) where every point is periodic, with the same period. However, these all come from composing the harmonic oscillator Hamiltonian with an area-preserving diffeomorphisms, meaning they are harmonic oscillators in a different set of coordinates.
We can make the \(U(1)\) action explicit by identifying phase space \(\mathbb{R}^2\) with the complex plane \(\mathbb{C}\), where \(x\) is the real part and \(p\) is the imaginary part. Realizing \(t \in U(1)\) as a unit norm element in the complex plane, the evolution \(\psi_t\) is multiplication by \(t\).
These equations naturally generalize to higher dimensions. in \(n\) dimensions, there are n position variables \(x_1, \dots, x_n\) with associated momenta \(p_1, \dots, p_n\), defining a point in phase space \(\mathcal{P} = \mathbb{C}^n\). The Hamilton equations on this phase space are
\[\begin{align} \dot p_{i}&= -x_i\\ \dot{x_{i}} &= p_i \end{align}\]The standard harmonic oscillator in \(n\)-dimensions is defined by a Hamiltonian
\[H = \sum_i x_i^2 + p_i^2\]But we notice this essentially describes \(n\) different, noninteracting harmonic osscilators. Leaning into this, we split \(H\) into consitituent parts: ^0da6d9
\[H= \sum_i H_i ,\qquad H_i = x_i^2 + p_1^2\]Each Hamiltonian \(H_i\) rotates its own factor of \(\mathbb{C}\) in phase space.
This procedure is ethos of Hamiltonian mechanics. Mechanics lives on phase space, whose structure converts a Hamiltonian function to a vector field, describing evolution under that Hamiltonian.
Symplectic Mechanics
%%==Cotangent bundle of spaces, inspired by pendulum==%%
Now we turn to geometry. We want to eventually replace the phase space \(\mathbb{C}^n\) with an arbitrary manifold \(\mathcal{P}\), and somehow define mechanics on \(\mathcal{P}\) that reduces to the hamiltons equations above in some coordinate chart. This is tricky with the coordinate-dependent formula [[2 A primer on geometric mechanics#^eq–Hamiltons]], so we need a coordinate invariant formulation. We achieve this using differential forms.
This finally motivates the phase space structure of a manifold \(\mathcal{P}\) is encoded in a 2-form \(\omega\), called the Symplectic form, Such that:
- \(\omega\) is nondegerenate, as a linear transform sending \(T^*\mathcal{P}\) to \(T\mathcal{P}\).
- \(\text{d}\omega = 0\).
The first condition ensures that there always exists a unique Hamiltonian vector field \(X_H\) such that \(\omega(X_H,-) = \text{d}H\). The second ensures that the sympletic form is locally modeled on the standard phase space. Closedness is necessary because the syandard symplecitc form \(\mathbb{C}^n\) is certainly closed, but remarkeably closeness is also sufficient. This is called [[Darboux’s theorem]]:
Theorem: (Darboux)
Let \((\mathcal{P},\omega)\) be a symplectic manifold. Each point \(p\in \mathcal{P}\), has a neighborhood \(U\) with coordinate chart \(\phi:U\to \mathbb{C}^n\) such that \(\omega\) is the pullback of the standard symplectic form on \(\mathbb{C}^n\). That is, \(U\) has coordinates \(q_i , p_i\) such that \(\omega = \text{d}q_1 \wedge \text{d}p_1 + \dots + \text{d}q_n \wedge \text{d}p_n\) ^thm–Darboux
This fact makes symplectic geometry feel significantly different from other sorts of geometry. Compare this with the analagous statement in Riemannian geometry: A metric can be put in the standard, euclidean form pointwise, but on an open neighborhood it can diverge from the standard due to its curvature. However, Darboux’s theorem says the standard form holds on the whole open est. There are no local invariants of a symplectic form akin to curvature. Said another way, all symplectic forms are locally isomorphic. This gives symplectic geometry a fundamentally globally character, to the point that the names “symplectic geometry” and “symplectic topology” are used interchangably.
Remark: Proof of Darboux’s theorem
You can find a proof of Darboux’s theorem in any book on symplectic geometry2, but to not leave you high and dry, let me give you the gist. We want to show any two symplectic forms on a small open set are equivalent by constructing a symplectomorphism: A diffeomorphisms pulling back one form to the other. (In particular, this can relate the given symplectic form to the standard one). We will instead look for an explicit path of diffeomorphisms, which is infinitesimally encoded in a time-varying vector field. A little manipulation shows this vector field satisfies a differential equation, which in fact is a version of Hamilton’s equations. By non-degeneracy, we know a solution to Hamilton’s equations exists, and we are done! Though constructing a whole path of diffeomorphisms seems like it would be harder, it lets us exploit the infinitesimal geometry that we know how to manipulate. This bit of slight-of-hand is called Moser’s trick. Symplectic geometry has many similar results turning structures into a standard form, all proven with a suitably generalized Moser’s trick.
Note that \(\omega\) as a matrix is skew-symmetric, since it comes from a 2-from. In particular, if \(n\) is odd, \(\omega\) must have an unpaired zero eigenvalue, and be degenreate. So, nondegenracy means that symplectic manifolds are always even dimsnional.
Example: Symplectic structure on \(S^2\)
The two dimensional sphere can be given a symplectic structure. Construct \(S^2\) as the set of vectors of unit length in \(\mathbb{R}^3\). For a vector \(p\) with unit length, the tangent space to the sphere is naturally the set of vectors normal to \(p\). A symplectic form takes two tangent vectors \(v,w\) and bilinearly returns a number. We define the standard symplectic form \(\omega_s\) using the cross product of vectors in \(\mathbb{R}^3\):
\[\omega_s(v,w) = ||v \times w ||\]This defines a two form because the cross product is bilinear and antisymmetric. As a two-form on a two dimensional manifold, it is necessarily closed. It is nondegenerate because any \(v\) has a \(w\) such that \(v \times w \neq zero\), for instance \(w = p\times v\). Hence, it is indeed symplectic.
Symmetries of Classical Mechanics
A symmetry of classical mechanics is a symmetry of phase space, which is a manifold with a symplectic structure. For a general manifolds, symmetries are Diffeomorphisms, differentiable bijective maps with differentiable inverses. These form a group where multiplication is composition of diffeomorphisms, which in particular has an infinitesimal structure. A path of diffeomorphisms can be described infinitesimally by a differentiable vector field, which points in the direction which points are pushed. Accordingly, pushing points along a fixed vector field \(X\) defines a family of diffeomorphisms, the flow \(\phi_X^t\) (This structure makes the group of diffeomorphisms an infinite dimensional Lie group).
The interesting group structure comes from the failure of commutativity, measured for diffeomorphisms \(a,b\) by their commutator \(a \circ b \circ a^{-1} \circ b^{-1}\). The infinitesimal structure of the group is encoded by the infinitesimal version of the commutator, called the Lie bracket
\[[X,Y] := \frac{\text{d}}{\text{d}s}\frac{\text{d}}{\text{d}t} \phi_X^t \circ \phi_Y^s \circ \phi_X^{-t} \circ \phi_Y^{-s} |_{s,t=0}\]This measures how one vector field changes along the flow of another. Taking the inverse of the RHS shows that the Lie bracket is antisymmetric, \([X,Y] = -[Y,X]\).The associativity of the group, encoded infinitesimally, enforces a condition on the Lie brackets called the Jacobi identity
\[[ [X,Y] , Z] + [ [Y,Z] , X] + [ [Z,X] , Y]=0\]The structure of a manifold are encoded in the Lie bracket on the space of vector fields, making this space into what’s called a Lie algebra.
Symmetries of a symplectic manifold are symmetries of a manifold that preserve the symplectic structure. These are diffeomorphisms \(\phi\) such that \(\phi^*\omega = \omega\), which are called Symplectomorphisms. Infinitesimally, these are vector fields \(V\) preserving the symplectic form, \(\mathcal{L}_V \omega = 0\). Using Cartan’s magic formula \(\mathcal{L}_ V = \text{d}\iota_V + \iota_V \text{d}\) and the fact that \(\text{d}\omega = 0\), \(V\) preserves \(\omega\) when \(\iota_V\omega\) is closed. Locally, these forms are equal to \(\text{d}H\) for some function \(H\), which by definition makes \(V\) a Hamiltonian vector field. That is, infinitesimal symmetries of a symplectic manifold are locally defined by smooth functions.
We can now pull back the Lie algebra structure from vector fields to their defining Hamiltonian functions. This is called the Poisson bracket, denoted by \(\{H,H'\}\). Just as the Lie bracket measures the change in one vector field under the flow of another, the Poisson bracket measures the change in one Hamiltonian under the flow of the other
\[\{H,H'\} \equiv \frac{\text{d}}{\text{d}t}\phi_{X_{H}}^t H' = X_{H}(H') = \text{d}H' (X_{H}) = \omega(X_{H},X_{H'})\]Note that the Poisson bracket is bilinear, by the linearity of the hamiltonian vector field. The antisymmetry of \(\omega\) means the Poisson bracket is antisymmetric, and a computation in coordinates verifies the Jacobi identity. So, the Poisson bracket makes the algebra of smooth functions on phase space into a Lie algebra. And indeed, the Poisson bracket on Hamiltonians is equivalent to the lie bracket on their vector fields:
\[[X_{H},X_{H'}] = X_{\{H,H'\}}\]Remark
We can think of the fundamental structure of classical mechanics as the algebra of smooth functions $C^\infty(M)$ with Poisson bracket (‘classical observables’). This alternate point of view to symplectic geometry gives a clear philosophical correspondence with quantum mechanics. There, the fundamental structure is the algebra of operators on a Hilbert space with commutator (‘quantum observables’). To ‘quantize’ a classical system, you associate a Hilbert space to a symplectic manifold, and construct a Lie algebra homomorphism from smooth functions with Poisson bracket to operators with commutator. In practice, this procedure can be rather difficult and is almost never possible in full generality, but that’s a story for another time.
The geometry of Harmonic Oscillators
[Last time](/blog/2022/07/24/symplectic.html), we introduced geometric mechanics and symplectic geometry. This will let us get at the mathematical structures hiding inside harmonic oscillators.Integral periods and circle actions
With this geometric formulation of classical mechanics in hand, let us look to higher dimensional harmonic oscillators. Imagine for instance a ball tethered to a spring in a plane. Throw it around a bit, see how it ticks:Its position is represented by a point \(\vec{q} \in \mathbb{R}^2\), and the spring applies a force \(-\vec{q}\). This force comes from a quadratic potential \(V(\vec{q})=\Vert \vec{q}\Vert ^2\). Phase space is \(T^{*\mathbb{R}^{2}}\cong\mathbb{R}^4\) with coordinates \(\vec{q},\vec{p}\), and the hamiltonian governing evolution is kinetic plus potential energy, \(H = \Vert \vec{p}\Vert ^2 + \Vert \vec{q}\Vert ^2\). Splitting into coordinates \(\vec{q} = (q_x,q_y)\), we see \(H = (q_x^2 + p_y^2) + (q_x^2 + p_y^2)\). Likewise, the symplectic form splits as \(\omega = \mathrm{d}q_{x}\wedge\mathrm{d}p_{y}+ \mathrm{d}q_{x}\wedge\mathrm{d}p_y\). Projecting onto the \(x\) or \(y\) components, we get 2D phase space and Hamiltonian \(H = (q^2 + p^2)\): The 2D oscillator is two independent 1D harmonic oscillators! We can write the phase space and Hamiltonian of a 2D oscillator as
\[\mathcal{P} = (\mathbb{C}^2,\omega_x+\omega_y) \qquad H = \Vert z_x\Vert ^2 + \Vert z_y\Vert ^2\]where \(\mathbb{C}^2\) splits into two copies, one for \(x\) and one for \(y\), with their respective coordinates \(z_{x},z_{y}\) and symplectic forms \(\omega_{x},\omega_{y}\).
Now lets take a closer look at the orbits. Here’s another ball to play with, but this time it predicts its trajectory. What shapes can you find?
All the orbits are ellipses! And in particular, they’re all periodic. This comes from the decomposition. Since Both the \(x\) and \(y\) oscillators have period 1, so too must their composite system. Evolution by time \(t\) is simply rotation of each of the factors of \(\mathbb{C}\):
\[(z_1,z_2) \to (e^{2 \pi i t} z_1,e^{2 \pi i t} z_2)\]so time evolution “rotates” \(\mathbb{C}^2\).
What if the \(x\) and \(y\) oscillators have different periods? Try changing the sliders above and see! If they’re integer multiples, a very similar thing happens. After enough time both \(x\) and \(y\) return to their starting position, so the orbit is periodic. It’s traces something fancier than an ellipse, called a Lissajous figure. To see that the \(x\) and \(y\) trajectories are indeed periodic, here are the projections to the component harmonic osscilators:
The time evolution is again rotation of each factor of \(\mathbb{C}\), now at different rates. The Hamiltonian \(H = \lambda_1^x\Vert z_x\Vert ^2 + \lambda_y^2\Vert z_y\Vert ^2\) gives frequencies \(\lambda_x\) and \(\lambda_y\), with time evolution
\[(z_x,z_y) \to (e^{2 \pi i \lambda_x t} z_x,e^{2 \pi i \lambda_y t} z_y)\]Any pair of integers \(\lambda_x,\lambda_y\) define a \(U(1)\) action on \(\mathbb{C}^2\). This straightforwardly extends to \(n\) independent oscillators, with phase space \(\mathbb{C}^n\) and relative frequencies encoded in an integer vector \(\vec \lambda \in \mathbb{Z}^n\).
Representations of \(U(1)\)
Harmonic oscillators don’t give just any \(U(1)\) action on \(\mathbb{C}^n\): They’re all linear. Encoding a point in phase space as a complex vector \(\vec{z} \in \mathbb{C}^n\), the \(U(1)\) action is multiplication by a matrix:
\[\begin{pmatrix} z_1 \\ \vdots \\ z_n \end{pmatrix} = \begin{pmatrix} e^{2 \pi i \lambda_1 t } & & \\ & \ddots & \\ & & e^{2 \pi i \lambda_n t } \end{pmatrix} \begin{pmatrix} z_1 \\ \vdots \\ z_n \end{pmatrix}\]The \(U(1)\) action comes from a representation \(\rho: U(1) \to GL(n,\mathbb{C})\). In fact, any such representation can be put in this form, choosing the right basis. This amounts to splitting \(\rho\) into a product of irreducible representations. Since \(U(1)\) is abelian, Schur’s lemma implies all irreducible representations are 1 dimensional. The linear maps \(U(1) \to \mathbb{C}\) are classified by an integer \(\lambda\) called the weight:
\[z \to e^{2 \pi i \lambda t z}\]So products of 1D representations are fully classified by their weight vectors \(\vec{\lambda} \in \mathbb{Z}^n\), and take the form above. The equivalence between harmonic oscillators with integer period ratios and linear \(U(1)\) representation is our first hint at the oscillator’s universal properties.
General circle actions
The notion of a circle action immediately extends to an arbitrary symplectic manifold \((\mathcal{P},\omega)\). Every element \(\theta\) of the group \(U(1)\) defines a diffeomorphism \(\phi_\theta : \mathcal{P} \to \mathcal{P}\), such that \(\phi_{\theta_1} \circ \phi_{\theta_2} = \phi_{\theta_1+\theta_2}\). That is, \(\phi\) gives a homomorphism from \(U(1)\) to the group of diffeomorphisms \(\mathrm{Diff}(\mathcal{P})\). When the \(U(1)\) action preserves the symplectic structure ( \(\phi_\theta^*\omega = \omega\) ), it is generated by a Hamiltonian: The infinitesimal action \(\frac{\text{d}}{\text{d} \theta} \phi_\theta\) is the Hamiltonian vector field for some function on phase space. Conceptually, a Hamiltonian \(U(1)\) action is a phase space symmetry.
==Regularity, isolated fixed points, etc==
Example: \(U(1)\) action on \(\mathbb{C}\)
\(\mathbb{C}\) carries a \(U(1)\) action via multiplication by unit norm complex numbers. The generating Hamiltonian is the harmonic osscilator Hamiltonian, \(\Vert z\Vert ^2\). Likewise, \(\mathbb{C}^n\) has a \(U(1)\) action generated by \(\lambda_1\Vert z_1\Vert ^2 + \dots + \lambda_n\Vert z_n\Vert ^2\) for \(\lambda_1, \dots, \lambda_n\) integers.
Example: \(U(1)\) action on \(S^2\)
The sphere \((S^2,\omega_S)\) described in [[2 A primer on geometric mechanics#^ex–S2-symplectic]] carries a natural \(U(1)\) action. Describing it as the unit sphere in \(\mathbb{R}^3\), rotation around the \(z\)-axis preserves the sphere. It also preserves \(\omega_S\), because the cross product \(v \times w\) only depends on the length of \(v\) and \(w\), and their relative angle. All of these quantities are preserved by rotation. The Hamiltonian generating this action is in fact z-coordinate of a point \(p \in S^2\), which you can think of as the height function on the sphere. Showing that this generates rotation is a very good exercise, but I explain this below the fold
Height generates rotation
The Hamiltonian evolution of \(h_z\) will necessarily preserve height, so the orbit of each point matches with the orbit under rotation. Furthermore, the velocity is proportional to the gradient of \(h_z\) along the sphere, which is uniform everywhere along each orbit. So, \(h_z\) must generate rotation on each layer of the sphere, and we need only check that each layer rotates with the same period. Denoting the azumithial angle by \(\phi\), the height function is \(\cos(\phi)\), so its gradient along the sphere has length \(\sin(\phi)\). However, each point must transverse a circle with radius \(\sqrt(1-h_z^2) = \sin(\phi)\), so the period (length over velocity) is \(2 \pi \sin(\phi) / \sin(\phi) = 2\pi\) for every height. Hence, \(h_z\) is the Hamiltonian generating rotation.
The Hamiltonian associated to a given circle action is often called the Moment map. This name originates from angular momenta, which generate rotation. However, angular momenta usually arise from rotations of configuration space \(M\), which lift to phase space \(T^*M\).
The duality between circle actions and their Hamiltonians is a classical manifestation of Noether’s theorem, where the circle action is a continuous symmetry and the moment map is the conserved quantity.
Universality of harmonic oscillators
A hamiltonian can only generate a \(U(1)\) action if every point is periodic with the same period, which is a very special condition. In a sense, this is the essence harmonic oscillators. We saw a hint of this in remark [[2 A primer on geometric mechanics#^rmk–harmonic-osscilator-periodic]], which said that the 1D oscillator was unique among circle actions on \(\mathbb{C}\), up to changes of coordinates. Any surface with \(U(1)\) action is locally modeled on the 1D oscillator.
Example: \(U(1)\) action on \(S^2\) as an oscillator
Consider the sphere with \(U(1)\) action described in example [[3 The geometry of harmonic oscillators#^ex–U1-action-S2]]. Each orbit is uniquely defined by the value of its Hamiltonian, equivently its height. We send the orbit at height \(t\) to the circle in \(\mathbb{C}\) with radius \(\sqrt{t}\), so that the Hamiltonian \(\Vert z^2\Vert\) on \(\mathbb{C}\) agrees with the Hamiltonian on \(S^2\).
==Finish this example, give the two coordinate charts: One for each critical point.==
==Describe fibration structure to image of moment map==
We see in this example that the dynamics around each critical point of the moment map on \(S^2\) correspond exactly to a harmonic oscillator. This is totally general: Just like symplectic manifolds are modeled on phase space (Darboux’s theorem, [[2 A primer on geometric mechanics#^thm–Darboux]]), symplectic manifolds with circle actions are modeled on harmonic oscillators. This is known as Equivariant Darboux’s theorem:
Theorem: Equivariant Darboux’s theorem
Let \((\mathcal{P},\omega)\) be a symplectic manifold with \(U(1)\) action defined by moment map \(\mu\). Each fixed point of the \(U(1)\) action has a neighborhood \(U\) equivalent to \((\mathbb{C}^n,\omega_{\textrm{s}})\) with \(U(1)\) action defined by moment map
\[H_{\vec{\lambda}} = \lambda_1\Vert z_1\Vert ^2 + \dots + \lambda_{n}\Vert z_n\Vert ^2 \qquad \vec{\lambda} \in \mathbb{Z}^n\]That is, there is a there is a symplectomorphism \(\phi:(U,\omega) \to (\mathbb{C}^n,\omega_{\textrm{standard})}\) such that \(\mu = H_{\vec{\lambda}} \circ \phi\)
This says that the neighborhood of a fixed point is equivalent to a harmonic oscillator, characterized by a weight vector \(\vec{\lambda}\). Note that the equality of the moment maps implies the \(U(1)\) actions are intertwined. If the flow under \(\mu\) is \(\rho_t\) and the flow under \(H_{\vec{\lambda}}\) is \(\rho^{\textrm{HO}}_t\), then \(\phi \circ \rho_t = \rho^{\textrm{HO}}_t \circ \phi\). The proof of theorem [[3 The geometry of harmonic oscillators#^thm–equivariant-darboux]] is a modified proof of vanilla Darboux’s theorem [[2 A primer on geometric mechanics#^thm–Darboux]]. It uses a version of Moser’s trick (described in remark [[2 A primer on geometric mechanics#^rmk–mosers-trick]]) that respects the \(U(1)\) action.
This is significant in a similar way to Darboux’s theorem. You would expect something like this to be true only infinitesimally, on the level of the linearized \(U(1)\) action on the tangent space. Indeed, this is the case for the equivalent statement in Riemannian geometry. But, the rigidity of symplectic geometry extends this linear action to a whole neighborhood of the fixed point.The behavior at the fixed points is global. The quadratic character of the moment map (the defining property of a harmonic oscillator Hamiltonian, and the reason that the \(U(1)\) action is linear) also extends globally. The \(U(1)\) action on \(\mathcal{P}\) is ultimately almost completely characterized by the collection of harmonic oscillators at each of the \(U(1)\) fixed points. This is why I say moment maps of circle actions are like global versions of harmonic oscillators. We will see several examples in the sequel where this philosophy is precise.
Torus action
Let us go back to our 2D oscillator example. All of these Hamiltonians with their different \(U(1)\) actions come from the same underlying structure. We see this by decoupling the oscillators. Imagine we fix the \(y\)-coordinate and only let \(y\) vary, alternatively fix \(x\) and let \(y\) vary. These give two independent \(U(1)\) actions on \(\mathbb{C}^2\), defined by Hamiltonians \(H_1 = \Vert z_1\Vert ^2\) and \(H_2 = \Vert z_2\Vert ^2\) respectively. The vector fields generated by these hamiltonians commute with one another, meaning the state after flowing for time \(t_1\) under \(H_1\) then time \(t_2\) under \(H_2\) equals that if you swap the order of the two flows. It is unambiguously defined by a pair of times \((t_1,t_2)\). Since each time is itself periodic, these flows define a \(U(1)^2\) action:
\[\rho_{(t_1,t_2)}: (z_1,z_2) \mapsto (e^{2 \pi i t_1} z_1,e^{2 \pi i t_2} z_2)\]This is a called torus action on \(\mathbb{C}^2\). Every linear circle action comes from combining these two basic Hamiltonians into a single hamiltonian. The flow under a hamiltonian \(H = \lambda_1 H_1 + \lambda_2 H_2\) composes a group homomorphism from \(\mathbb{R}\) to \(U(1)^2\) with the torus action:
\[t \to (\lambda_1 t, \lambda_2 t) \qquad \Phi^t_H = \rho_{(\lambda_1 t, \lambda_2 t)}\]When \(\lambda_1,\lambda_2\) are integers this is a homomorphism \(U(1) \to U(1)^2\), so the flow is periodic and we retrieve the circle action described in [[3 The geometry of harmonic oscillators#Integral periods and circle actions]].
Similar statements hold for \(n\) independent oscillators, phase space is \(\mathbb{C}^n\) and each oscillator oscillates one copy of \(\mathbb{C}\), giving an action of \(U(1)^n\) on phase space. Let us generalize this to an arbitrary symplectic manifold. Suppose we have a collection of Hamiltonian \(H_1, \dots H_n\), each the moment map of some \(U(1)\) action, normalized to have the same period. We demand the \(H_i\) pairwise Poisson commute, \(\{H_i,H_j\}=0\) (See section [[2 A primer on geometric mechanics#symmetries of classical mechanics]]). This means their associated flows commute, so evolution by time \(t_i\) under each Hamiltonian \(H_i\) gives a uniquely defined flow, characterized by the n-tuple of times \((t_1, \dots, t_n)\). This defines a \(U(1)^n\) action. Following the analogy that the \(H_i\) are global versions of harmonic oscillators, this collection of Hamiltonians is a global version of \(n\) independent harmonic oscillators.
Following our 2D oscillator example, we can build whole families of Hamiltonians by weighting the periods of each oscillator relative to one another, setting \(H = \lambda_1 H_1 + \dots + \lambda_n H_n\) for \(\lambda_i \in \mathbb{R}\) (for \(\lambda_i \in \mathbb{Z}\), the resulting flow is a \(U(1)\) action.) Our \(H_i\) satisfy \(\{H_i,H_j\}=0\), so \(H_j\) is conserved under the flow of \(H_i\) and vice versa. In particular, every \(H_i\) is conserved under our linear combination of basic hamiltonians \(H\). This means we have \(n\) conserved quantities, representing the energy of the \(n\) harmonic oscillators. Thought of as a vector \(\vec{H} = (H_1, \dots, H_n)\), this defines a function \(M \to \mathbb{R}^n\) called the moment map of the \(U(1)^n\) action.
Example: \(U(1)^2\) moment map of 2D oscillator
To demonstrate this, we return as always to the 2D oscillator. The Hamiltonians are \(H_1 = \Vert z_1\Vert ^2\) and \(H_2 = \Vert z_2\Vert ^2\), which generates rotation in each \(\mathbb{C} \times \mathbb{C}\). Fixing the value of the moment map fixes the radii \(r_1\) and \(r_2\) for each coordinates. This is certainly preserved under rotation. We project to the position plane by taking the real coordinates of both. As a point evolves under a weighted sum \(aH_1 + bH_2\), the \(x\)-coordinate oscillates between \(\pm r_1\) and the \(y\) coordinate between \(\pm r_2\). The specific coefficients \(a,b\) dictate the periods of each.
==Example program?==
The torus action preserves the value of the moment map, which lets us decompose phase space into slices \(\vec{H}^{-1}(t)\) for \(t\in \mathbb{R}^n\). We can understand phase space by understanding these two aspects: The image of the moment map, and the structure of the slices. The full description will occupy another few posts, but let us get a taste from a few examples:
Example: 1D oscillator
The 1D oscillator has phase space \(\mathbb{C}\) and moment map given by the harmonic oscillator hamiltonian \(\Vert z\Vert ^2\). The image consists of positive real numbers \(\mathbb{R} \geq 0\). The slice above \(r\) has two behaviors:
- The slice above \(r > 0\) is the circle of radius \(\sqrt{r}\)
- The slice above \(0\) is the origin, the fixed point of the \(U(1)\) action. We can think of \(\mathbb{C}\) as a circle fibration above \(\mathbb{R}\geq 0\), where the circle collapses at \(r=0\).
==Add cone picture==
Example: 2D oscillator
The image of the moment map is the image of \((\Vert z_1\Vert ^2,\Vert z_2\Vert ^2)\), which is the first quadrant of \(\mathbb{R}^2\), where \(\{(r_1,r_2) | r_i\geq 0 \}\).
- When both \(r_i\) are positive, the slice is a product of circles with radii \(\sqrt{r_1}\) and \(\sqrt{r_2}\). Or, a torus!
- On the boundary where \(r_2=0\), the slice is a product of a circle of radius \(\sqrt{r_1}\) and a point. Projecting to position space, the oscillator is fixed to the \(x\)-axis. It is preserved under the second \(U(1)\) action. Similarly, above the boundary \(r_1=0\), the oscillator lives on the \(y\)-axis.
- The corner \(r_1=r_2=0\) is a fixed point of the torus action, where the oscillator sits unmoving at the origin. The full phase space \(\mathbb{C}^2\) can be thus built as a degenerating torus fibration above \(\mathbb{R}_{\geq 0}^2\). Once circle degenerates on \(\mathbb{R}_{\geq 0} \times 0\), the other on \(0 \times \mathbb{R}_{\geq 0}\), and both above \((0,0)\).
==Add simulation, where you select value of moment map and see how the orbit changes==
We can construct a \(U(1)\) action on \(\mathbb{C}^2\) as a sub-torus of our \(U(1)^2\) action. We build the moment map from the 2D moment map as \(H = H_1 + H_2 = \Vert z_1\Vert ^2 + \Vert z_2\Vert ^2\). The image of \(H\) consists of \(\mathbb{R}_{\geq 0}\), and the pre-image of a point \(r>0\) is a 3-sphere in \(\mathbb{C}^2\) with radius \(r\). At \(r=0\), this three-sphere degenerates to the origin. This is the unique fixed point of the \(U(1)\) action.
Example: \(S^2 \times S^2\)
consider the product \(S^2 \times S^2\), with \(U(1)\times U(1)\) acting by the standard \(U(1)\) action on each copy of \(S^2\) with moment map the height function. Since the flow of one moment map leaves the other sphere fixed, the moment maps commute. The possible values of both Hamiltonians forms a square \([-1,1]^2\). The pre-image of a point \((x,y)\) in the square is a product of circles at height \(x\) and \(y\) respectively. There are three possibilities:
- When \((x,y)\) is in the interior of the square, the preimage is a torus.
- When it lies on an edge, the preimage is a circle on one sphere and a pole of the other. One of the \(U(1)\) actions fixes these points.
- When it lies on a corner, the preimage is a point sitting on the pole of both spheres. both \(U(1)\) actions fixes these points.
Generalizing this, \({S^2}^n\) carries a natural \(U(1)^n\) action, with moment map taking values in \([-1,1]^n\).
We see some common themes: Polygonal moment map images, with co-dimension \(k\) faces whenever exactly \(k\) of the \(U(1)\) factors is fixed.
Something special happens when the dimension of phase space is double the number of commuting Hamiltonians. We will see that the torus acts freely on the pre-image of a generic point of the moment map. With \(n\) dimensions of moment map and \(n\) dimensions of torus, this entirely accounts for the \(2n\) dimensional manifold. So, the slice must be exactly a torus. Said another way, every oscillator contributes 2 degrees of freedom: It’s energy, and its phase angle. \(n\) oscillators exhausts all \(2n\) degrees of freedom, so at fixed energies the state is exactly specified by \(n\) phase angles, and the inverse image of a generic moment map is \(U(1)^n\). These phase spaces are called Toric manifolds. They are entirely characterized by their \(n\) independent \(U(1)\) actions.
Spaces of orbits
U(1) orbits
Let \((\mathcal{P},\omega)\) be a symplectic manifold with a \(U(1)\) action generated by moment map \(H\). This means every point belongs to a periodic orbit on the flow under \(H\). What is the space of orbits? Can we divide \(\mathcal{P}\) by \(U(1)\)? This is always possible if \(U(1)\) acts freely, but for compact \(\mathcal{P}\) the \(U(1)\) action necessarily has fixed points (The global minima and maxima of \(H\)). Fixed points generally ruin the topology of orbit spaces, as single orbits can be adjacent to whole families of fixed points, resulting in a non-hausdorff topology. We avoid this by noticing that all orbits must have constant value of \(H\), so it makes sense to look at orbits on \(H^{-1}(c)\). If \(H\) has no critical points with value \(c\) (meaning \(c\) is a regular value of \(H\)), then \(U(1)\) acts freely on \(H^{-1}(c)\) and its space of orbits is a manifold. Thus we define the symplectic quotient (Or Marsden-Weinstein quotient)
\[\mathcal{P} // U(1) \equiv H^{-1}(c)/U(1)\]Vitally, this quotient carries a natural symplectic form, induced from that on \(\mathcal{P}\). The reduced form is defined by lifting vectors from \(H^{-1}(c)/U(1)\) to \(H^{-1}(c)\) by arbitrarily choosing a basepoint and a value in the \(U(1)\)-direction, then plugging these into the usual symplectic form. This is well defined because the symplectic form is preserved by \(U(1)\) so the basepoint doesn’t matter. The \(U(1)\) direction is in the null space of the symplectic form, so t)$$ direction, so those component of the vector don’t matter.
Notice that the symplectic quotient reduces the dimension by two: Not only does it remove a factor of \(U(1)\), but it restricts to a level set of the moment map. The symmetry acts twice as much as you’d naïvly expect, hence the double-slash notation. (These double-acting symmetries are a very general phenomena in symplectic geometry.) Perhaps one could think of this as “removing one harmonic oscillator”, first fixing its energy then dividing out by its phase degree of freedom.
Orbits of a 2D oscillator
Consider once again phase space \(\mathbb{C}^2\), with \(U(1)\) action generated by \(H = \Vert z_1\Vert ^2 + \Vert z_2\Vert ^2\). For a regular value, say a, \(H^{-1}(1)\) is the unit 3-sphere. Since \(\text{d} H\) does not vanish on \(H^{-1}(1)\), by general grounds \(U(1)\) must act freely on \(S^3\). In particular, there is a fibration
\[\require{AMScd} \begin{CD} U(1) \cong S^1 @>>> S^3;\\ @. @VVV \\ @. S^3/S^1; \end{CD}\]The only fibration of \(S^3\) by \(S^1\) is the famous Hopf fibration, with base \(S^2\). So, the space of orbits is a 2-sphere. But seeing is believing: the Hamiltonian \(H = \Vert z_1\Vert ^2 + \Vert z_2\Vert ^2\) represents a 2D harmonic oscillator with equal periods, with orbits that are ellipses. Let’s look at the ellipses with constant energy:
(Simulation is here, yet to be incorperated)
First we fix the value of the \(U(1)^2\) moment map, and understand the space of orbits. he pre-image of a generic value of the moment map is a torus \(U(1)^2\), as described in [[#^ex–2d-oscillator-torus-fibration]]. \(H\) generates a \(U(1)\) subgroup, so the space of orbits of \(H\) is the complementary copy of \(U(1)\): It is a circle. We can visualize this with a trick:make the period of one oscillator (say, the \(x\)-oscillator) ever so slightly sorter than the other. Once \(y\) has made a full orbit, \(x\) won’t quite line up, so the orbit’s phase in \(x\) rotates slightly. This orbit tightly spirals around the torus, eventually wrapping it densely. (In general, any Hamiltonian whose orbit densely fills a torus is called almost-periodic. For a 2D oscillator this happens when the ratio of periods is irrational). Tracking the orbit for one y-period, this acts just like a slowly varying \(U(1)\) orbit in \(U(1)^2\)
==add picture of torus==
(Simulation is here, yet to be incorperated)
It looks like a circle in 3D, slowly rotating around the \(y\) axis! Every orbit, the \(x\)-phase of each point in the orbit increases by a small angle, so they slowly traces an \(x\)-oscillator orbit. This is especially clear when we mark a point. So, it slowly rotates. The “z-axis” it rotates through is the x-momentum.
(Simulation is here, yet to be incorperated)
Now we return to visualizing the orbits of a level set for \(H = \Vert z_1\Vert ^2 + \Vert z_2\Vert ^2\). The equation \(H=1\) defines a line in the values of the \(U(1)^2\) moment map \((H_1 = \Vert z_1\Vert ^2, H_2 = \Vert z_2\Vert ^2)\) as shown below. The space of orbits in \(H^{-1}(1)\) is composed of the space of orbits for all allowed values of the moment map. For most values of \((H_1,H_2)\) this is a circle, but this is not true at the boundaries. When \(H_1=1, H_2=0\), the orbit is purely in the x-axis, and is fixed by rotation – the circle of orbits degenerates to a point. Likewise when \(H_1=1, H_2=0\) the orbit lies in the \(y\) axis, and the circle again degenerates. Thus, we see a sphere. And indeed, showing all these orbits at once, they trace out a sphere in 3D on front of our eyes!
(Simulation is here, yet to be incorperated)
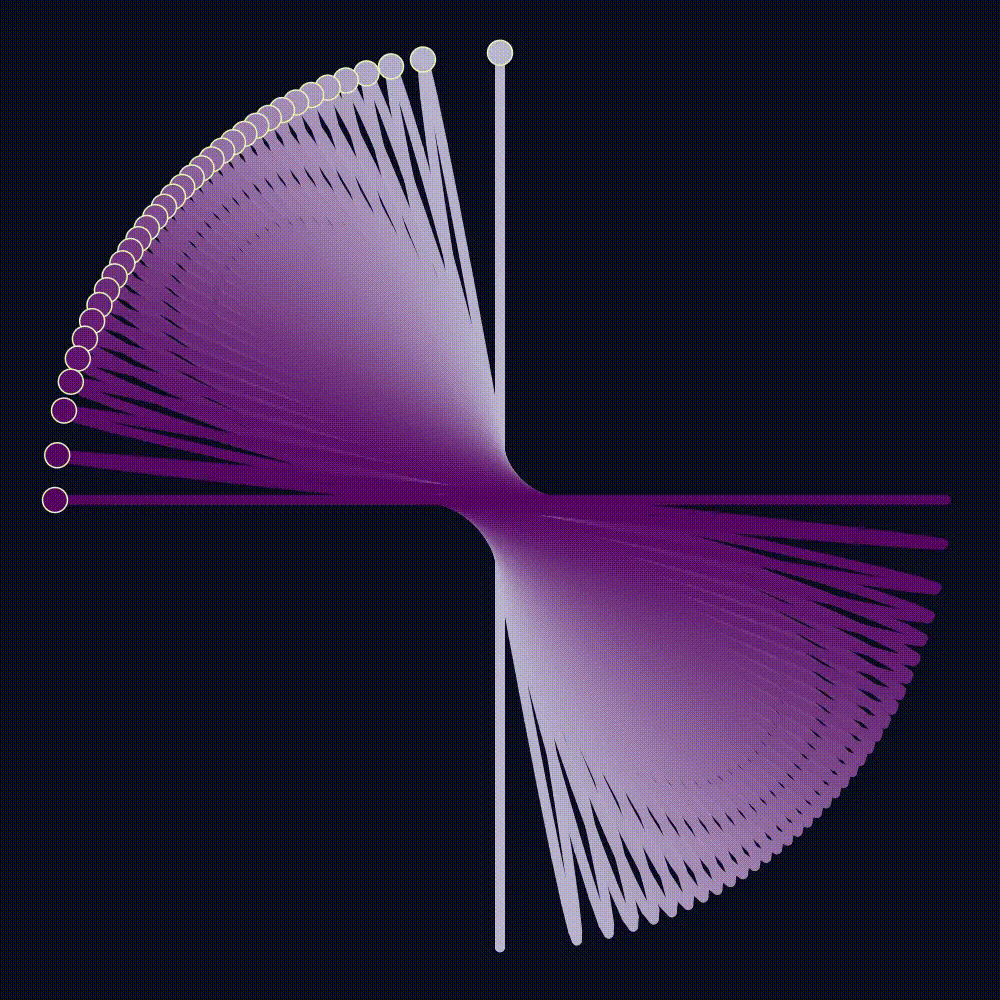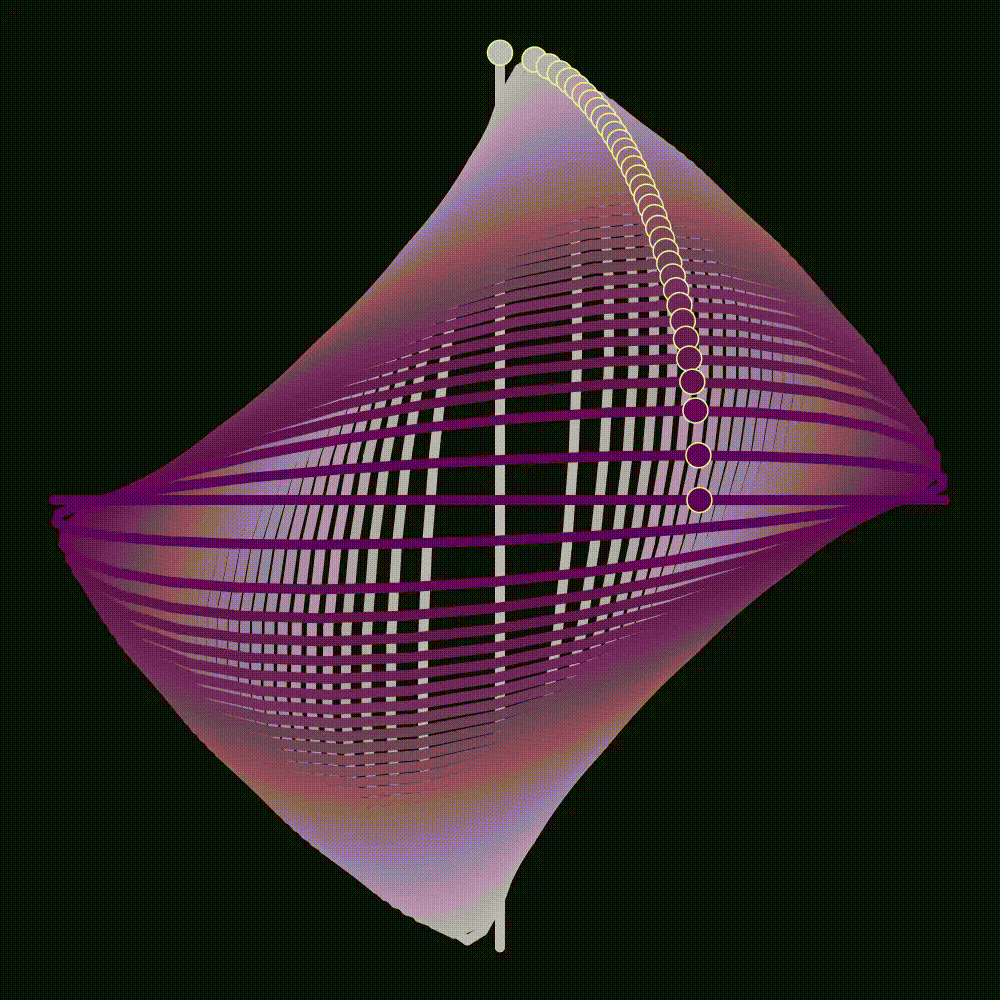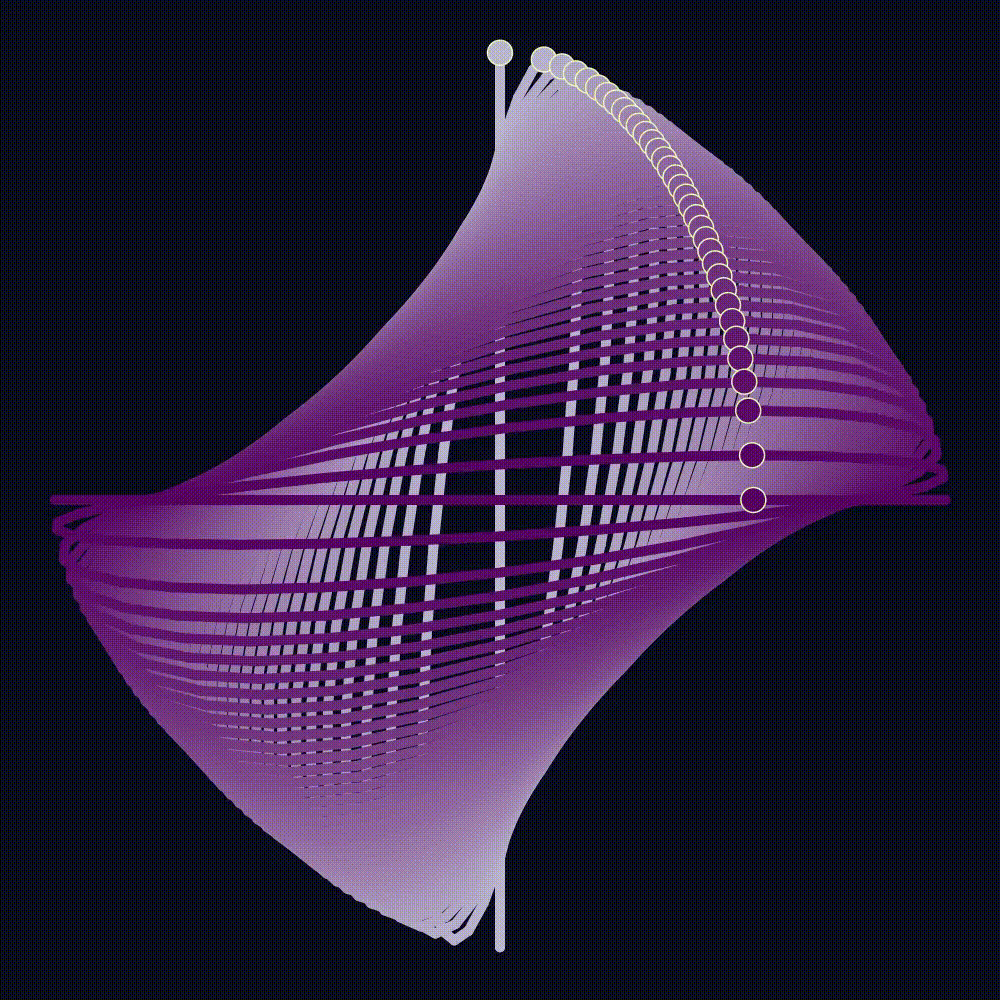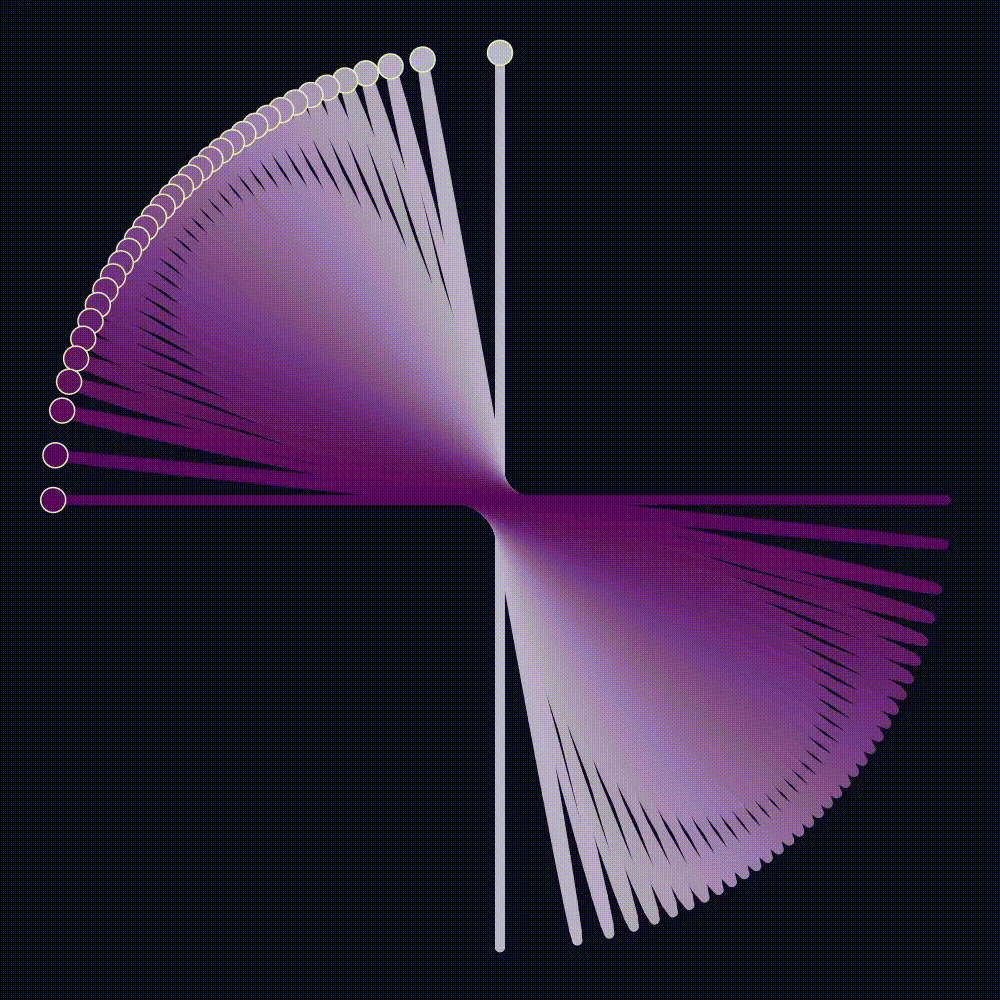
Recalling example [[#^ex–U1-action-S2]], the construction of the space of orbits is identical to \(S^2\) as a fibration, according to its standard \(U(1)\) moment map. The height function for the space of orbits is \(H_1 - H_2\), which is \(1\) at \((1,0)\) and \(-1\) at \((0,1)\). Its image is naturally identified with the intersection of the line \(H_1+H_2 = 1\) with the allowed values of the moment map. Said another way, the moment map of the sphere of orbits is just the cross-section of the higher dimensional moment map! Our trick perturbing the \(x\)-period essentially added an extra Hamiltonian \(\epsilon H_1\) to the flow of \(H\). Since \(H_1\) is conserved under \(H\) it descends to a function on the space of orbits, and so it induces a flow. (Incidentally, this relation between dynamics of the full space and dynamics on the space of orbits is the source of the reduced symplectic form.) Projecting onto the cross-section, \(H_1\) is proportional to the height function, so its flow is rotation. This is why we see rotation of the sphere.
Our choice of \(x\)-perturbation instead of \(y\) was arbitrary. A \(y\) perturbation rotates points about the \(y\) axis, instead of the \(x\). But, the function \(-H_2\) projects to an identical function as \(H_1\) on the cross-section. So, they give the same function on the sphere, and have the same dynamics: Rotation through the space of orbits. This remarkably means that the evolution of ellipses could either be a circle rotating in 3D around the Y-axis, or the X-axis!
(Simulation is here, yet to be incorperated)
This becomes more mind-bending with other \(U(1)\) generating Hamiltonians, like \(H'=3H_1 + 2H_2\) shown below. Once again, both \(x\) and \(y\) perturbations generate identical dynamics (up to scale) on the space of \(H'\) orbits. We can produce the resulting evolving curve as the shadow of a wire-sculpture in 3D rotating around the \(x\)-axis, or a Different wire sculpture rotating around the \(y\)-axis. Your brain can see either! This is called the Dual-Axis illusion, and it won the 2019 best illusion of the year award. It works because of toric geometry, for the shape is the orbit of a slightly perturbed periodic 2D harmonic oscillator. I suspect harmonic oscillator orbits are the only family of shapes with this dual-axis property, but I’m not sure.
\(U(1)\) orbits on toric manifolds
When the Hamiltonian \(H\) is defined from a \(U(1)^n\) moment map, we can do the symplectic reduction in stages. First, the level set of \(H\) is a cross-section of the image of the \(U(1)^n\) moment map. Second, the \(U(1)\) acts only on the fibers of the moment map. When the manifold is toric, the fibers are \(U(1)^n\) and it is very easy to divide out by \(U(1)\): You get the complementary subgroup \(U(1)^{n-1}\) of \(U(1)^n\). The resulting manifold is still toric. Instead of the original \(n\)-dimensional space of Hamiltonians, we get the \(n-1\) dimensional orthogonal complement to the Hamiltonian we reduced with. The tori are generated by the flows of these remaining Hamiltonians.
Symplectic reduction gives us some more exciting examples of toric manifolds:
Example: \(\mathbb{C} P^n\) as a toric manifold
Consider \(n\) harmonic oscillators, with phase space \(\mathbb{C}^n\) and the usual \(U(1)^n\) action. The [[Moment map]] \(H = \Vert z_1\Vert ^2 + \dots + \Vert z_n\Vert ^2\) generates a \(U(1)\) subaction. What is the space of orbits of \(H\) with energy 1? The \(U(1)\) action generated by \(H\) is multiplication by an overall phase
\[(z_1, \dots , z_n) \mapsto e^{2 \pi i t} (z_1, \dots , z_n)\]The space of orbits is complex vectors of norm 1 modulo phase. Equivalently, the Symplectic reduction is \(\mathbb{C}^n - \{0\}\) modulo the overall scaling action of \(\mathbb{C}^*\). The quotient is called Complex projective space \(\mathbb{C} P^{n-1}\).
\(\mathbb{C} P^{n-1}\) has an induced toric structure from \(\mathbb{C}^n\). The image of the \(U(1)^n\) moment map is \(\mathbb{RR}_{\geq 0}^n\). Reducing by \(H\) selects the subspace \(H_1 + \dots + H_n =1\), which is isomorphic to the image of the moment map of \(\mathbb{C} P ^{n-1}\). In particular, the moment map image is an \(n-1\)- dimensional simplex. For \(\mathbb{C} P^2\), this can be written as the triangle in \(\mathbb{R}^2\) with corners \((0,0), (1,0),\) and \((0,1)\).
Orbits of general groups
The machinery of symplectic reduction works for arbitrary group, though it is somewhat easier to state for \(U(1)^n\). Suppose a symplectic manifold \(\mathcal{P}\) has symmetry represented by a Lie group \(G\), meaning \(G\) acts on \(\mathcal{P}\) and preserves the symplectic form. We further assume \(G\) is a Hamiltonian action, meaning its infinitesimal flows are generated by Hamiltonian functions. The infinitesimal flow is represented by a homomorphism from the lie algebra \(\mathfrak{g}\) (The infinitesimal symmetries of the group) to the lie algebra of vector fields on \(\mathcal{P}\) (The infinitesimal symmetries of the manifold structure on \(\mathcal{P}\)). We (by assumption) have a hamiltonian function \(H_g\) for \(g \in \mathfrak{g}\). However, The transformations from \(\mathfrak{g}\) to vector fields to hamiltonian functions, so \(H_g\) must be linear in \(g\). Therefore, we define the Moment map of a general group
\[\mu:M \to \mathfrak{g}^* \qquad \mu(x)g = H_g(x)\]The moment map is a machine for converting an element of a lie algebra into the Hamiltonian which generates the associated flow. In our case with \(U(1)^n\), the Lie algebra is \(\mathfrak{u}(1)^n \cong \mathbb{R}^n\). Since \(U(1)^n\) is abelian, its lie algebra has trivial lie bracket. So, the moment map is a map \(\mu:\mathcal{P} \to \mathbb{R}^n\) such that each factor commutes with one another, i.e it is described by \(n\) commuting Hamiltonians. We can define symplectic reduction: if \(0 \in \mathfrak{g}^*\) is a regular value of \(\mu\), then \(G\) acts freely on \(\mu^{-1}(0)\), so we define
\[\mathcal{P} // G \equiv \mu^{-1}(0) / G\]All of the results in this paper extend in one way or another to general groups. For the most part, we will stick with $U(1)^n$.