BPS states, Seiberg-Witten theory, and Integrable systems
Summary:
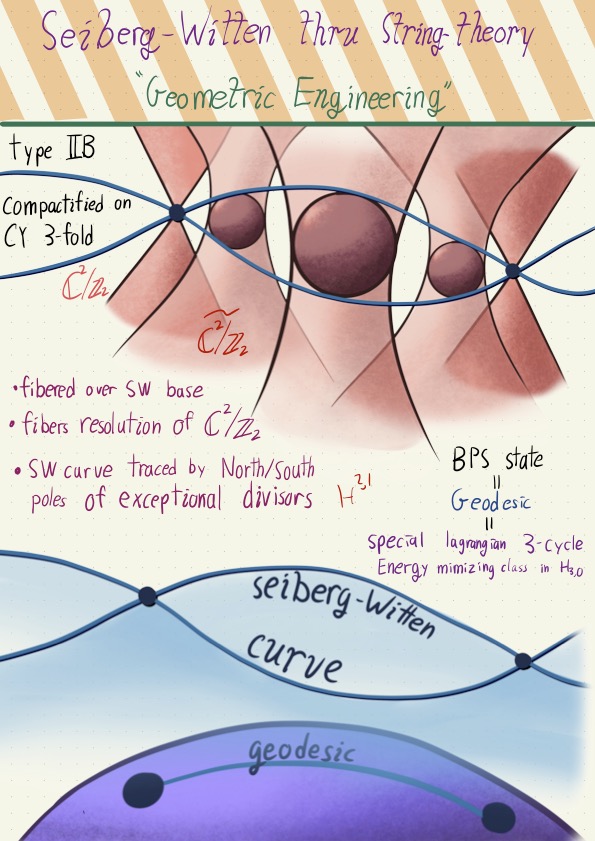
a trilogy of talks that all explore the power of BPS states in math and physics. First, I relate the BPS representations of supersymmetric algebras with BPS monopoles. Second, I go through Seiberg and Wittens solution for the low energy effective field theory of N=2, D=4 super yang mills. Vitally, they use the topological aspect of BPS states to pull back a lattice from the free theory to the whole vacuum moduli space, giving an integrable system. Third, I give a unified description of BPS states as variations of hodge structures, and discuss how various avatars of BPS states fit in to the story.
Presented at:
File: ⭐"꙰"꙰"꙰"꙰"꙰"꙰"꙰"꙰⭐
