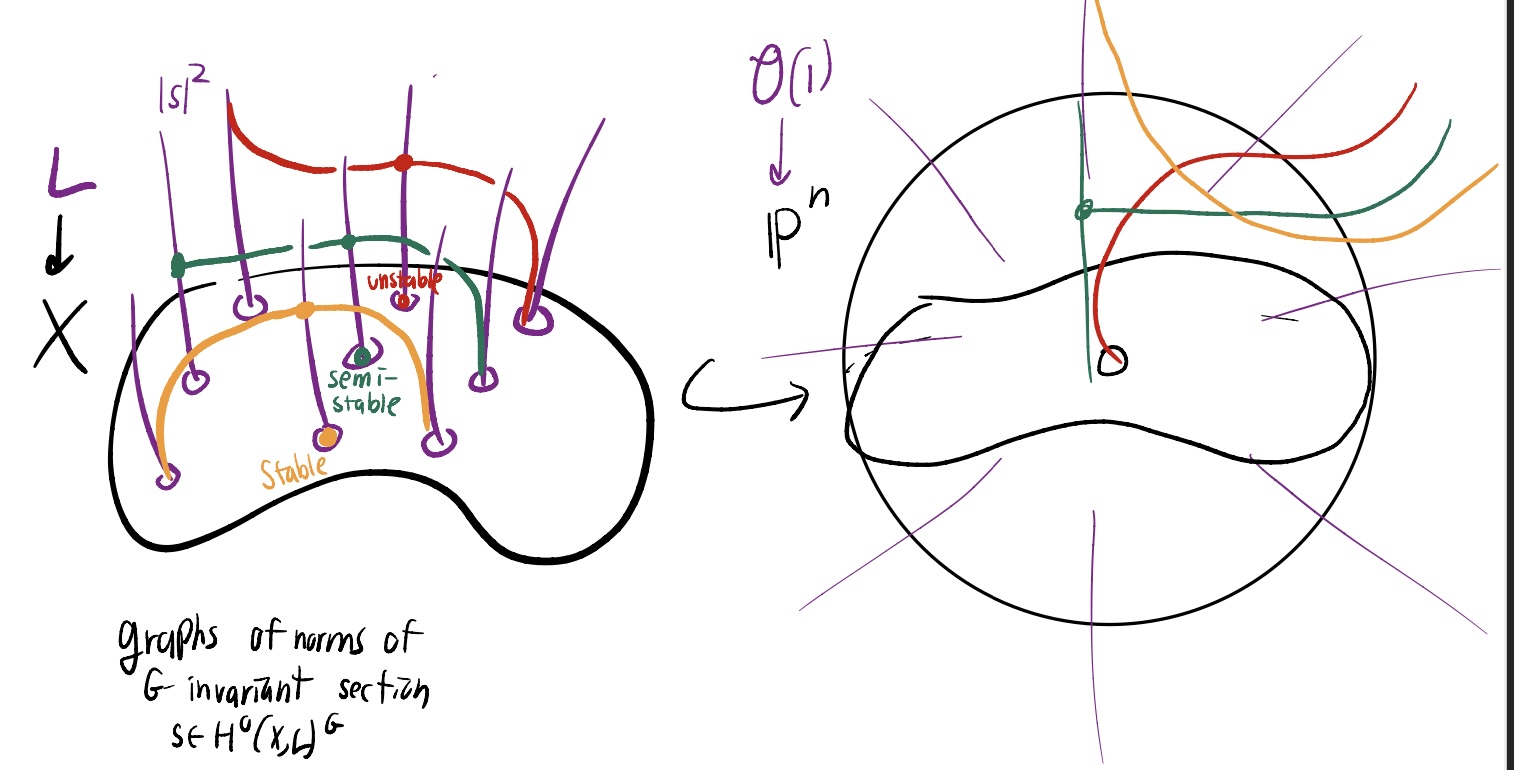
Kempf-Ness theorem and quantization

Nov 2024

talk

Summary:

In symplectic geometry, groups act twice. When we take a symplectic reduction, first we demand the moment map equals zero, then we divide by the group. Instead we can form the symplectic reduction as the quotient by the complexified group. This is formalized by the Kempf-Ness theorem: Symplectic quotients equals GIT quotients.

Geometric quantization turns a symplectic manifold into a hilbert space. If we quantize a manifold with a G-action, quantization gives us a representation of G. This plays nice with symplectic reduction, as formalized in the Guilleman-Sternberg conjecture: The quantization of the reduced space is the G-invariants of the quantization.

These two mottos are the same idea in disguise.

Presented at:

Student symplectic seminar

File: ⭐"꙰"꙰"꙰"꙰"꙰"꙰"꙰"꙰⭐

I learned most of this talk from the lecture notes Moment Maps and Geometric Invariant Theory by Chris Woodward. He takes a GIT first approach, and talks about quantization commutes with reduction comparatively briefly. For the proof of quantization commutes with reduction, I followed:

Guilleman and Sternberg’s original 1982 paper, Geometric quantization and multiplicities of group representations
This was re-exposited by Qiuyu Ren in Quantization Commutes with Reduction, which is useful to have in parallel.

Finally, I found Richard Thomas’s Notes on GIT and symplectic reduction for bundles and varieties useful. This is where I got the thumbnail picture.