A and B models: The story of mirror symmetry

Nov 2020

talk expository slides

Summary:

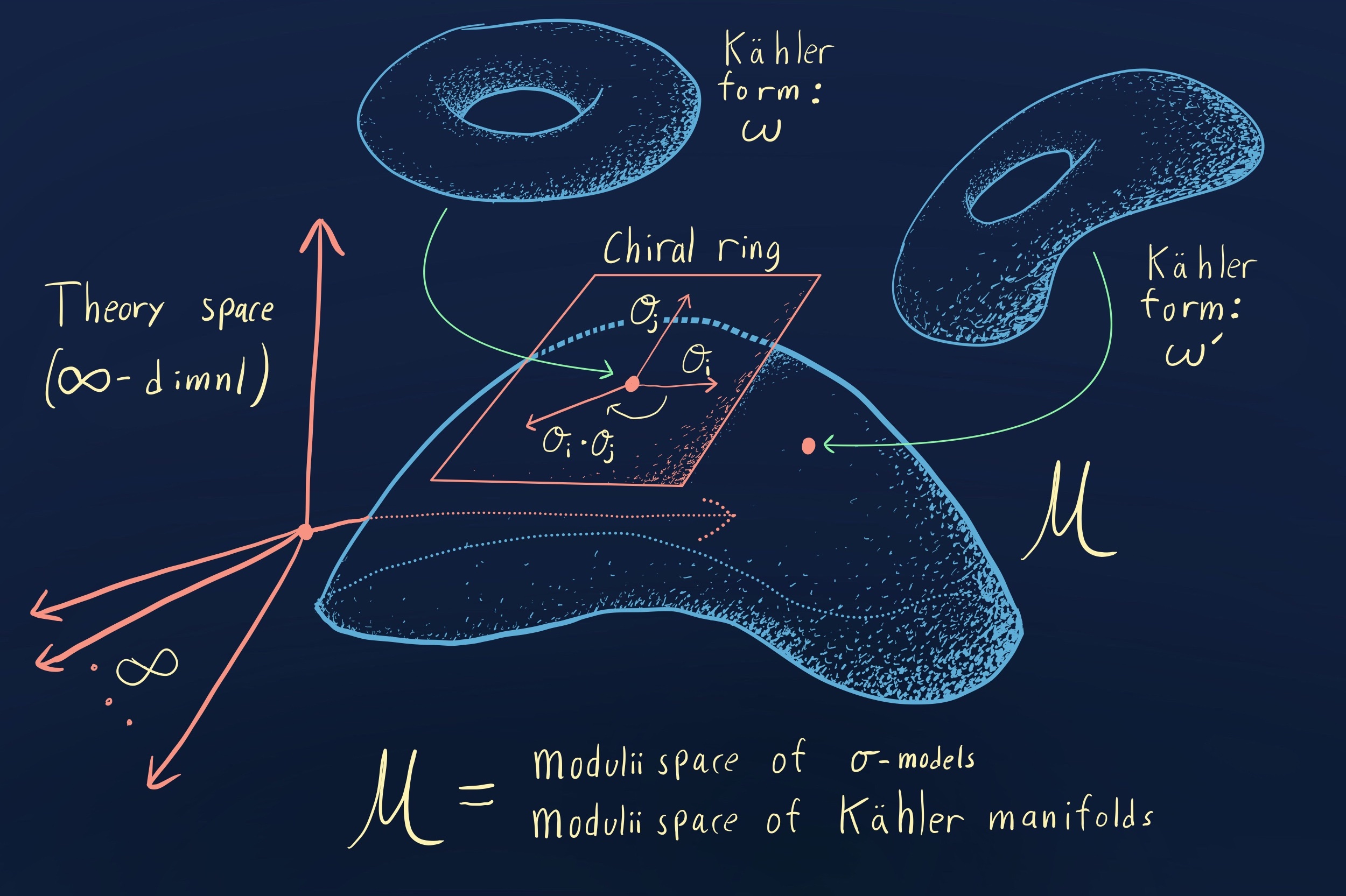
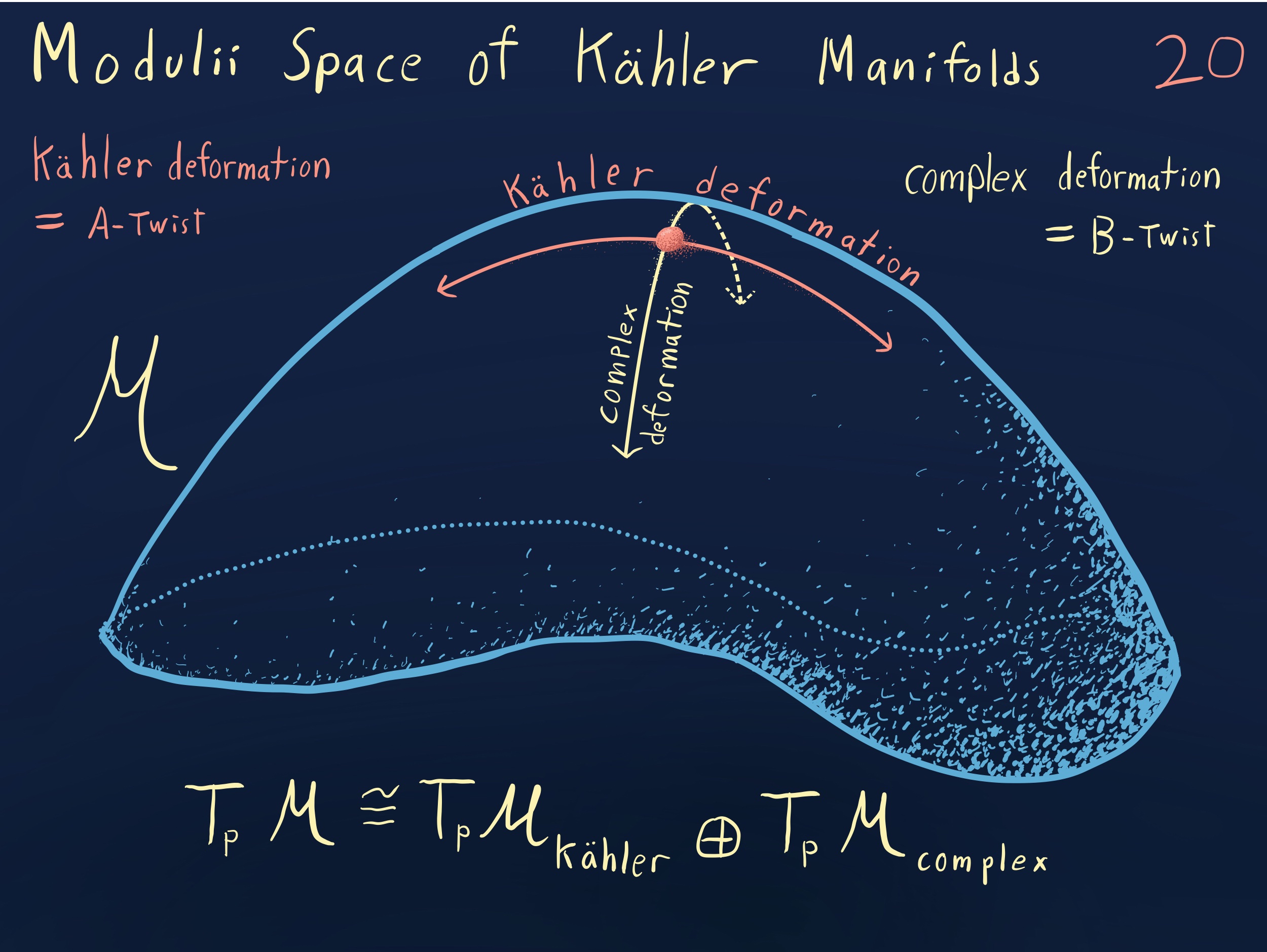
This talk states mirror symmetry, framed as a conjecture about the equivlence of two frobenius manifolds. Two sorts of ‘topological twisting’ should give equivlent topological field theories. The first gives the A-model, which is a path integral counting holomorphic curves in a kahler manifold. The second gives the B-model, a Landau-Ginzburg theory whose physics depends on the singularity structure of a holomorphic function. Underlying both is the structure of a frobenius manifold– Mirror symmetry conjectures that its the same structure

Presented at:

UMD RIT in geometry and physics, Fall 2020