Understanding hamiltonian G-spaces through quantization
Summary:
Philosophically, quantization converts functions on symplectic manifolds to operators on Hilbert spaces in a structure-preserving way. A symplectic manifold carrying a structure-preserving \(G\)-action quantizes to a \(G\)-action on the Hilbert space, or a representation of \(G\). Using this, we can study representations through the geometry of symplectic manifolds. After outlining this philosophy, I describe a parallelism between symplectic manifolds and representations. Coadjoint orbits are irreducible representations, the moment map is a decomposition into irreducible representations. Constructions which engineer new representations become blueprints for building new symplectic manifolds. These constructions motivate hyperspherical varieties, the class of spaces starring in relative langlands duality
Presented at:
- UC Berkeley geometric representation theory seminar, fall 2023
🔗 Link to file
Dictionary between symplectic manifolds and representations
Over the course of these two talks, I outlined a parralelism between symplectic manifolds and representations. This is built upon a collection of results, which I want to collect all in one place. If there’s anything I’ve left off, please let me know!
I’ll be starting with the standard dictionary provided by geometric quantization. this procedure is a beautiful idea which only half works, and needs a bunch of extra structures and requirements for things to make senes. See, for example, Lectures on geometric quantization, by Bates and Weinstein for details and caveats.
| Classical mechanics | Quantum mehanica | Source |
|---|---|---|
| Symplectic manifold $(M,\omega)$ | Hilbert space $\mathcal{H}(M)$ | |
| Algebra of smooth functions $C^\infty(M)$ with poisson bracket | algebra of linear operators $\mathcal{H}(M) \to \mathcal{H}(M)$ with commutator | |
| $T^*X$ | $\mathcal{H}(T^*X) = L^2(X)$ | Geometric qunatization with a real polarization. This was understood since the dawn of quanutm mechanics, with the work of Weyl |
| $(M,\omega)$ compact kahler, with line bundle $L$ with curvature $\omega$ | $\mathcal{H}(T^*X) = H^0(M,L)$ | Geometric quantization with complex polarization. This was developed by Konstant and Souriau in the 70’s, to generalize Kirillov’s orbit method (see below) |
Now we introduce $G$-actions, one preserving the symplectic structure on $M$, and its induced linear action on the hilbert space $G\circlearrowright \mathcal{H}$. The results below paint a picture of old-school picture of geometric quantization as an extention of the orbit method. The fundamental structure is the moment map $\mu: M \to \mathfrak{g}^\ast$ defining the $G$-action on $M$, which equivariantly relates $G\circlearrowright M$ to the coadjoint action $G\circlearrowright \mathfrak{g}^*$. The coadjoint orbits provide a natural way to decompose $M$. To be safe, we’ll assume $G$ is compact reductive, but many of the facts are more general.
| symplectic geometry (Classical) | representation theory (Quantum) | Source | |
|---|---|---|---|
| Hamiltonian action $G \circlearrowright M$ | A $G$-representation $G\circlearrowright \mathcal{H}$ | ||
| Moment map $\mu:M \to \mathfrak{g}^*$ | Decomposition of $\mathcal{H}$ into irriducible representaionts | ||
| $\mathcal{O}_\alpha$ through point $\alpha$ in the dual of the cartan subalgebra | $E_\alpha$, The irriducible representation of heighest weight $\alpha$ | This is the heart of Kirillov’s orbit method, developed through the 60s and 70s. See Kirillov’s book on the orbit method. In the complex polarization, the hilbert space is $\mathcal{H}(\mathcal{O}_\alpha) = H^0(\mathcal{O_\alpha},L_\alpha)$. By the Borel-Weil theorem, this is an irriducible representation of $G$ with weight $\alpha$. | |
| the image of $\mu(M)$ contains a coadjoint orbit $\mathcal{O}_\alpha$ | $G \circlearrowright \mathcal{H}$ contians the irriducible representation $E_\alpha$ with nonzero multiplicity | Proven in GS821 for compact Kahler manifolds | |
| Symplectic reduction $M// G = \mu^{-1}(0)/G$ | $\mathcal{H}(M//G) = \mathcal{H}(M)^G$, the $G$-invariant vectors in $\mathcal{H}$ | Quantization commutes with reduction. This was first proven in GS821 for compact Kahler manifolds, and has since been widely generalized. | |
| $M$ multiplicity free: $M//_\alpha G = \mu^{-1}(\mathcal{O}_\alpha)/G$ has dimension 0 for all $\alpha$ | $\mathcal{H}$ is multiplicity free: Each irrep appears in $\mathcal{H} = \bigoplus_{\alpha}E_\alpha^{n_\alpha}$ 0 or 1 times | Proven for $M = T^\ast X, \mathcal{H} = L^2(X)$ by GS842 | |
| for all $G$-invariant functions $f,g \in C^\infty(M)^G, \quad \{f,g\}=0$ | For all $G$-invariant operators $A,B: \mathcal{H}\to \mathcal{H}$, $[A,B]=0$ | This is equivlent to multiplicity-freeness, by an easy argument first given by GS83a3 | |
| The action of $G \times G$ on $T^*G$ on left and right is multiplicity free | $G \times G \circlearrowright L^2(G)$ decomposes as $\bigoplus_\alpha E_a\otimes E_a^\ast$ (the peter-weyl theorem) | This is the prototypical multiplicty-free behievor. This fact is used in GS842 to prove the general case that multiplicity free manifolds have multiplicity free representations | |
| Symplectic induction: If $H \circlearrowright S$ is a hamiltonian $H$-space, and $H < G$ we can build a hamiltonian $G$-space $\text{h-ind}_H^G(S) = (S \times T^* G) //H$ | if $V$ is a representation of $H \subset G$, we can build the induced representation $ind_H^G(V)$ | This was floating around for a while before being formalized. One early use is in KKS784 | |
| Hamiltonian restriction For $G\circlearrowright M$ hamiltonian, $H < G$, we can treat $M$ as an $H$-space | For $H< G$ and a represetation $\rho: G \circlearrowright \mathcal{H}$, we have the restricted represetation $Res^G_H(\rho): H \circlearrowright \mathcal{H}$ | ||
| $\text{Hom}_G(X,\text{h-ind}_H^G Y) = \text{Hom}_H(\text{res}^G_H(X),Y)$ where $Hom_G(X,Y) = (X^- \times Y) //G$, $X^-$ the reversed symplectic form. | Frobenius reciprocity: for $\rho$ a $G$-rep and $\psi$ an $H$-rep, $\langle Ind_H^G \psi,\rho \rangle_H = \langle \psi, Red_H^G\rho \rangle$ |
This was first noticed in a specific case in KKS784, but is discussed in much more detail in GS83b5. There it is proved for coadjoint orbits, and the form written here comes from RZ206 |
References:
-
Geometric quantization and multiplicities of group actions, Guillemin and Sternberg, 1982 ↩ ↩2
-
Multiplicity-free spaces, Guillemin and Sternberg, 1984 ↩ ↩2
-
On collective complete integrability according to the method of Thimm, Guillemin and Sternberg, 1983 ↩
-
Hamiltonian group actions and dynamical systems of calogero type, Kazhdan, Konstant and Sternberg, 1978 ↩ ↩2
-
The Frobenius reciprocity theorem from a symplectic point of view ↩
-
Symplectic Induction, Prequantum Induction, and Prequantum Multiplicities, Ratiu and Ziegler, 2020 ↩
Gallery
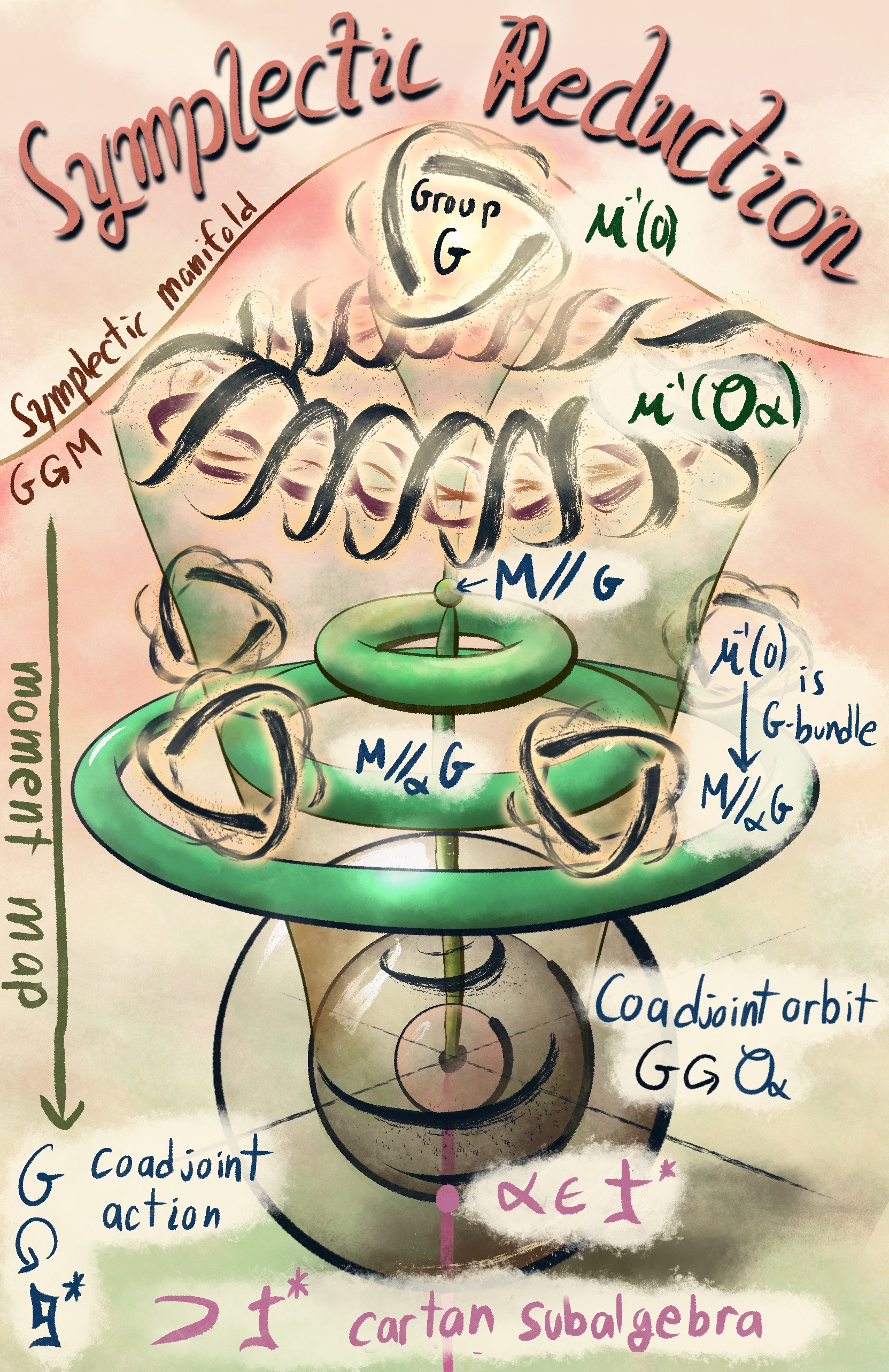
Anatomy of a symplectic manifold
This illustration explains the structure of a symplectic manifold with symmetries. Symplectic reduction is a procedure which “divides out” the symplectic manifold by those symmetries, producing a lower-dimensional symplectic manifold. When I think of symplectic manifolds, I feel how the swirling dynamics of a group splits the manifold into digestible symplectic reductions. This drawing is my best approximation of that vision, an MRI of the anatomy underneath every symmetric symplectic manifold.
Here is the technical explination. The picture shows the splitting of a symplectic manifold $M$ with hamiltonian $G$ action into slices via its moment map $\mu:M \to \mathfrak{g}^*$. The $G$-action on $M$ is equivariantly mapped to the coadjoint action $G\circlearrowright \mathfrak{g}^\ast$. The $G$-invariant sets on $\mathfrak{g}^\ast$ are the coadjoint orbits $\mathcal{O}$. The fibers $\mu ^{-1} (\mathcal{O})$ are $G$-bundles over the symplectic reductions $M //_\mathcal{O} G = \mu^{-1}(\mathcal{O})/G$.
This picture is inspired by the group of rotations in 3D space $G=SO(3)$. The group is rendered as a atomic nucleas, to illistrate the three perpendicular rotations which generate the 3-dimensional group. The moment map sends $M$ to $\mathbb{R}^3$, which is acted on by $SO(3)$ by rotation. So, the coadjoint orbits are spheres centered around zero, as seen in the bottom half of the picture. Choosing a maximal torus ammounts to fixing an axis of rotation. Here, I chose the z-axis. The tori in the middle of the picture represent the symplectic reduction of the origional manifold $M$ at different levels. The inky swirls above the tori represent the dynamics of the action of $G$ on the slices $\mu^{-1}(\mathcal{O}_\alpha)$.
Geolocation
This piece appeared in the JMM 2024 Math art exhibit