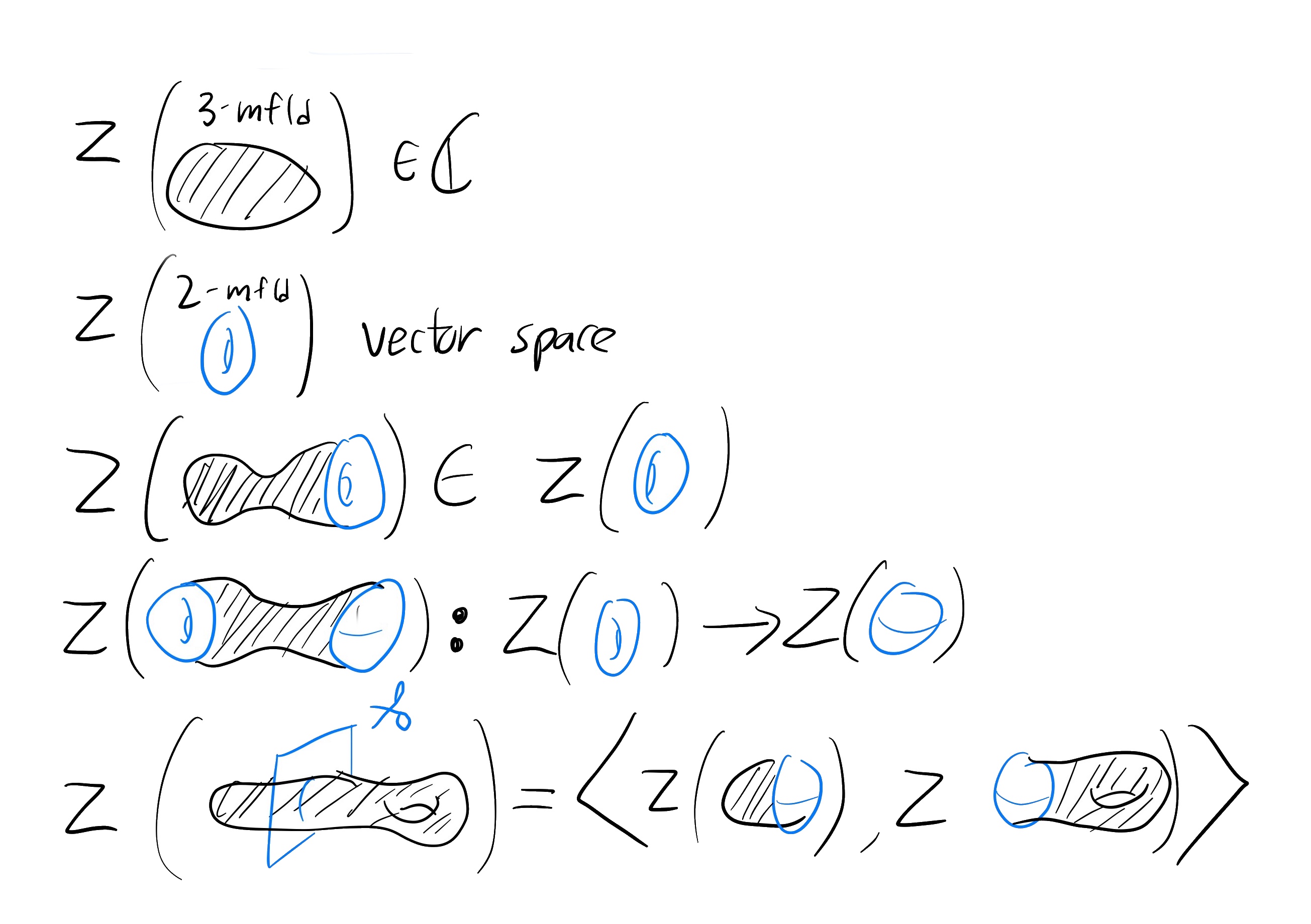Chern-simons theory and the Jones polynomial

Oct 2023
talk

Summary:

Knots were born from Kelvin’s vortex theory of atoms. This was a bold (if ultimately misguided) attempt to quantize physics through the topology of knots. Following the steady march of mathematical progress, knots strayed far from their physical roots. I describe a curious rondevouz in the 1980s, when a modern incarnation of Kelvin’s vortex theory once again spurred knot theory, now through the jones polynomial. I give two talks summarizing this story, and Witten’s paper on quantum field theory and the jones polynomial.

Presented at:

  • UC Berkeley Jones polynomial learaning seminar, fall 2023

File: ⭐"꙰"꙰"꙰"꙰"꙰"꙰"꙰"꙰⭐

Chern-simons theory and the Jones polynomial

The first week, I traced through this perspective on the simplest knot invariant, the linking number. I start from winding numbers in 2D, explained through flat connections on a line bundle. Extending to 3D, this gives gauss’s integral formula for linking numbers. Then I introduce the ableian chern-simons functional integral, and show that it formally computes linking numbers. Finally, I construct this as a topological quantum field theory, giving a way to compute linking numbers from knot diagrams.

The second week, This week, we will instead integrate over lie algebra-valued 1-forms (nonabeilain Chern Simons theory), and show that the resulting topological invariant is the jones polynomial. To do so, we introduce the axioms of topological quantum field theory, which gives a calculate the invariant by cutting up the manifold into small pieces. This shows us how our invariant changes when resolving a crossing in a knot, reproducing the skien relations of the Jones polynomial.

Here are some sources which I used for this talk.