TQFT structure of Gromov-Witten theory and the Seidel representation
Summary:
First, I describe the TQFT structure of the topological sigma model with target a symplectic manifold. To a surface, the TQFT assigns gromov witten invariants. To a circle, it assigns quantum cohomology. To a point, it assigns the fukaya category. I describe the origin of quantum cohomology from the top down (by neck-stretching curves and using gromov-witten invariants) and bottom up (as the Hochschild cohomology of the Fukaya category).
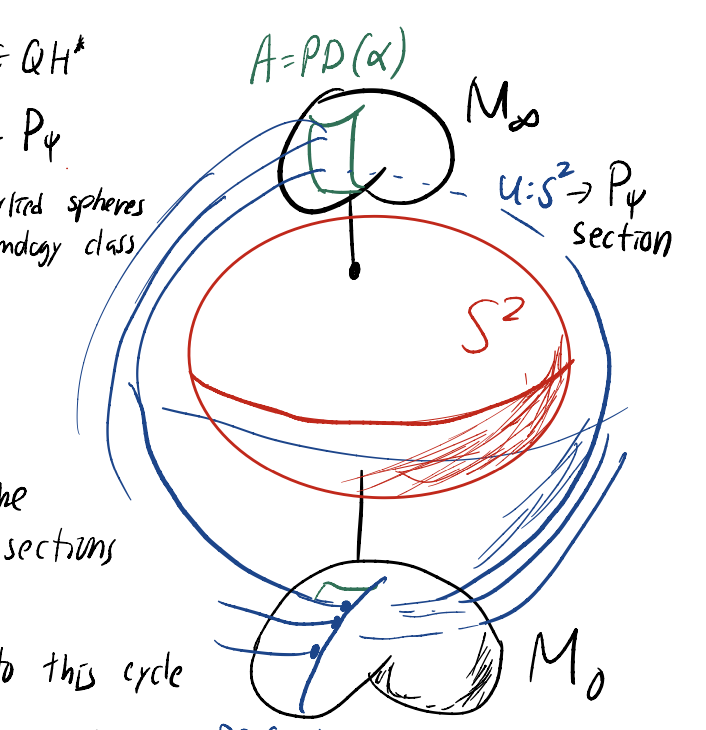
Next, I discuss the Seidel representation. Given a loop $\Psi_t$ of hamiltonain diffeomorphisms, Seidel constructs a unit in the quantum cohomology ring, the “seidel element” $S(\Psi_t)$. An element of quantum cohomology is acted on by $\Psi_t$through multiplication by $S(\Psi_t)$. Seidel constructs $S(\Psi_t)$ by building a symplectic bundle over $\mathbb{P}^1$ with clutching function $\Psi_t$, then counting $J$-holomorphic sections. This is the first taste of the categorical action of Hamiltonian diffeomorphisms on the fukaya category.
Presented at:
- gauged TQFTs seminar , Spring 2025
🔗 Link to file
Sources
TQFT structure
Witten 1988, Topological sigma models
- This paper is why Gromov-Witten theory has witten’s name. It describes how the Gromov-witten invariants arise from observables in the topological A-model. This paper also counts $J$-holomorphic sections with a wink, “this will probably have some geometric applications”. The first of these applications was Seidel’s paper.
I don’t know a good refrence for the fully extended TQFT structure that I described. But, when trying to get quantum cohomology as $Z(S^1)$, I found these math overflow questions helpful
- Hochschild (co)homology of Fukaya categories and (quantum) (co)homology
- Comparison between Hamiltonian Floer cohomology and Lagrangian Floer cohomology of the diagonal
Seidel representation
Seidel 1995,pi_1 of symplectic automorphism groups and invertibles in quantum homology rings
- Original source for Seidel’s representation. My goal was to explain this paper in the context of this seminar.
Mcduff, Salamon: J-holomorphic curves and Quantum cohomology.
- Example 8.6.1 and section 11.4, 12.5
- Textbook refrence for Seidel’s representation, and the main thing I followed