The Riemann-Roch Theorem

Nov 2020
talk expository slides

Summary:

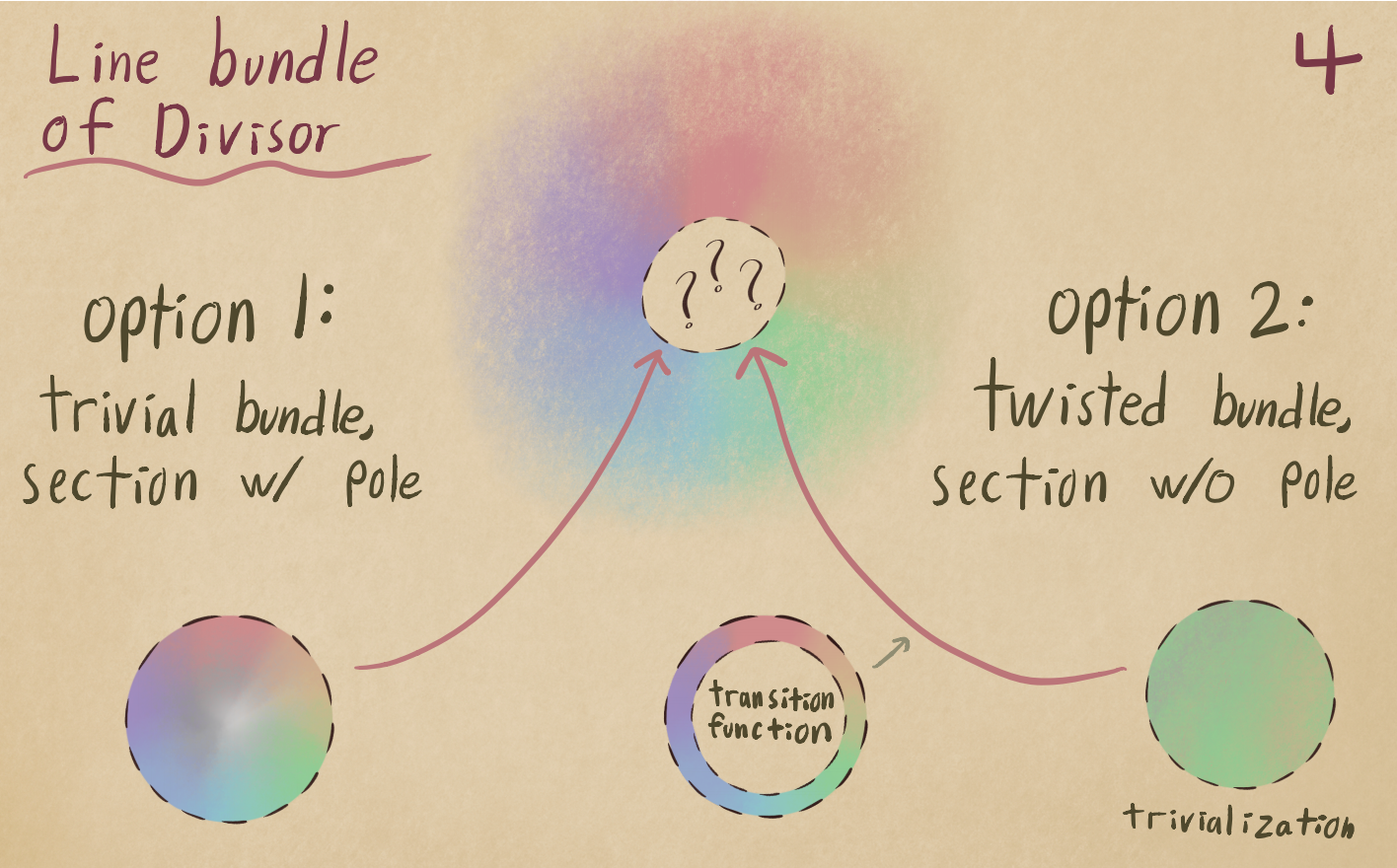
The Riemann-Roch theorem gives the number of linearly independent holomorphic sections to a line bundle. I explain morally why divisors should correspond to line bundles, and present the usual sheaf-theoretic derivation of Riemann-Roch. But to me, Riemann-Roch relates the solutions of differential equations to the genus, bridging analysis and toppology. This was my first intoxicating taste of the Atiyah-Singer index theorem

Presented at:

  • MATH742, Geometric analysis, UMD, Fall 2020

File: ⭐"꙰"꙰"꙰"꙰"꙰"꙰"꙰"꙰⭐

The Riemann-Roch Theorem