Math crafts: How things curve

This is a 1-unit course, meeting on Thursdays 4-6pm.
First class is Thursday, Jan. 18. To enroll, please fill out this google form before Wednsday evening, Jan. 24. Remember to use your Berkeley email address.
Overview
How do things curve? How can you build things that curve? More fundamentally, what does it mean to curve? This course will take a hands on, intuitive approach to these questions. We will follow two parallel paths:
- Crafts: To understand geometry with our hands, we will build many curved spaces. Each one uses different craft mediums and exemplifies techniques for creating curvature.
- Math: The mathematical framework for exploring curvature is called differential geometry. We will build an informal understanding of two dimensional geometry, including the shape of curved surfaces and the counterintuitive life of an ant on a curved surface.
We will explore, we will discover, and we’ll have fun! Each class, we’ll build an arts and crafts project illustrating that day’s topic. For more open-ended exploration, there will be 3 mini-projects over the semester. These go deeper into the crafts and topic from class. At the end of the semester, everyone will bring their mini-projects for a class-wide show and tell.
The course is meant as a general-education math course. Coming from math, this course illustrates geometry emphasizing physicality and intuition. Coming from art, this course is a friendly, visual introduction to some beautiful ideas not seen until upper level math classes. If this sounds interesting and fun, then this course is designed for you!
Weekly schedule
Click on the the activity for worksheet with answers
Class 0, 1/18
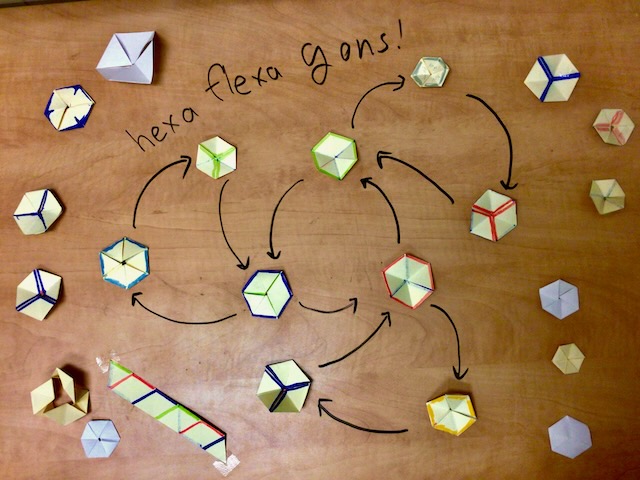
Flexagon detectives
Summary:
Craft: Make paper hexaflexagons, curiously folded paper strips
Math: How does one think about and analyze math crafts?
Class 1, 1/25
Interlocking Paper Polyhedra
Summary:
Craft: cut out slide-together polygons out of construction paper. Assemble these into polyhedra!
Math: Discover the platonic solids, and the rules governing what faces can fit together to make convex polyhedra. Study the angular defect around each vertex.
Class 2, 2/1
Weaving Pipe Cleaners
Summary:
Craft: weave pipe cleaners into mats. Discover how singularities in the weaving pattern forces the mat to curve in 3D.
Math: Examine how adding extra angle around a vertex produces negative curvature. See the shape the negative curvature imposes.
Class 3, 2/8
Hyperbolic Flexors
Summary:
Craft: Build flexible cardbord models of the hyperbolic, and see how they contort to fit into three dimensional space
Math: Examine the consequences of many hyperbolic verticies attached together. Look into the size and shape of a section of the hyperbolic plane.
Class 4, 2/15
String art and 2D curvature
Summary:
Craft: sew thread through evenly spaced holes around the perimeter of a circle according to a simple pattern. Connect each hole to the hole a constant rotation around the circle. Observe the emergent circular patterns.
Math: relate the radius of a polygon to its side length and angles. Understand curvature of a curve as angle per unit distance.
Class 5, 2/22
Due: Mini-project 1
Hyperbolic origami
Summary:
Craft: Create origami models of hyperbolic space.
Math: examine how to approximate negative curvature using zero-curvature paper. Understand negative curvature as an excess of space, and as a deficet of angles.
Class 6, 2/29
Can you make a paper sphere?
Summary:
Craft: Create origami with curved creases, and see what sorts of forms we can make. Can we fold a sphere? How close can we get?
Math: Introduce gaussian curvature. The curved origami produces developable surfaces, which are surfaces with zero gaussian curvature. Examine the possible forms of these developable surfaces.
Class 7, 3/7
Soap films part 1, curvature of foams
Summary:
Craft: Blow bubbles! 3D bubbles, 2D bubbles, and foams of bubbles
Math: examine the structure of compound bubbles and their curvature. Determine the simple laws governing soap films, known as Plateau’s laws. Relate curvature to the physics of surface tension and air pressure.
Class 8, 3/14
Soap films part 2, minimal surfaces
Summary:
Craft: Play with bubble wands. Understand how the shape of a frame controls the shape of a bubble film stretched across the frame.
Math: Relate bubble films to minimal surfaces. Describe minimal surfaces in terms of principle curvatures. Understand the gaussian curvature of minimal surfaces.
Class 9, 3/21
Ruled surfaces
Summary:
Craft: Using skewers and rubber bands, build wodden models of the hyperbolic paraboloid and the hyperboloid.
Math: Create ruled surfaces, surfaces made by tracing out lines. Analyze their gaussian curvature. Make doubly ruled surfaces, and observe how they flex.
Class 10, 4/4
Due: Mini-project 2
Curvature from strips
Summary:
Craft: Taping together strips of paper, assemble positivly and negativly curved surfaces.
Math: Understand geodesic curvature of curves on surfaces. On constant curvature surfaces, see how the area enclosed by a curve controls its curvature
Class 11, 4/11
from 3D to 2D and back
Summary:
Craft: Peel oranges and potatoes. Learn how to build 3D objects by folding up 2D patterns. To build the 2D model of the object, cover it with masking tape, then cut the tape off and lay it flat.
Math: Understand how to manifest curvature in objects, combining geodesic cuvautre and angle defect together. Learn how map makers make maps, and the various tradeoffs required.
Class 12, 4/18
Living in curved space
Summary:
Craft: play more with orange peels. Walk around in simulations of spherical and hyperbolic space (image to right from game hyperbolica). How does it feel to live in a curved space?
Math: Learn about monodromy, how walking in a circle in curved space causes you to rotate. Use this to recontextualize everything in the class.
Class 13, 4/25
Curvature and holes!
Summary:
Math: Learn about the gauss-bonnet theorem, relating the number of holes in an object to its total curvature. See this from multiple perspectives. The Euler formula for polyhedra relates angle defect to topology. The geodesic curvature of triangles on the surface relates total rotation to topology. The monodromy perspective relates topology to the experience of an ant walking along the surface.
Class 14, 5/01
Due: Mini-project 3
Show and tell! Bring all 3 of your mini projects to class, and show them off.