Flexagon detectives
Summary:
Craft: Make paper hexaflexagons, curiously folded paper strips
Math: How does one think about and analyze math crafts?
Summary
Welcome to math crafts! Today we will build our craft detective hats. Math crafts are not shaped by hand, but instead are built following regular patterns. The shapes emerge themselves. We will practice identifying underlying patterns, and thinking about how the shape manifests. First we examine a few crafts we will build later in the semester, as an amuse bouch. Then, you will get a object, and try to build it yourself. No instructions, only detective skills.
Materials and setup
Materials
Each table of 5 will need:
- A tape dispenser
- Scissors
- 20 strips of paper (5 per student). Each 3/4” wide by 11” long. I used cardstock since I had it, but printer paper is fine.
- One tri hexaflexagon, and one hexahexaflexagon
For the class, you should have some extra printer paper on hand.
Setup
Its important that each strip is cut with straight, parallel lines. My building had a guillotine paper cutter, which made the job efficient.
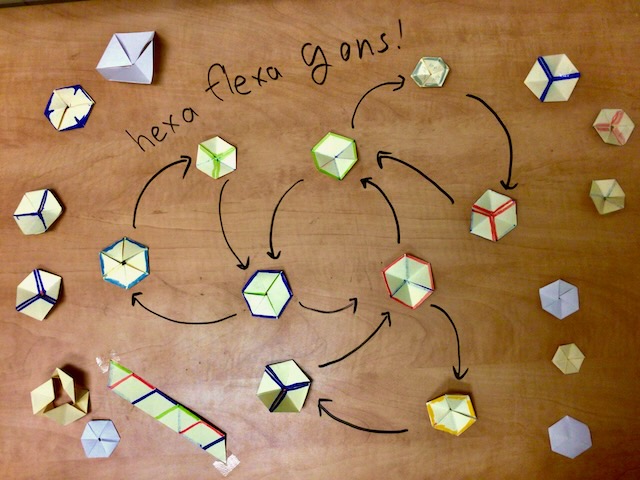
You can learn about hte hexaflexagon in the perenial youtube video by Vi Hart. To make the hexahexaflexagons, follow these instructions. Make sure to color each side beforehand, so you’ll need 6 different colors of markers. For a class of 20, you’ll need 5 hexaflexagons and 5 hexahexaflexagons. This is actually a bit of a project. It took me and a friend 2 hours.
Class
Icebreaker
I started class by randomly grouping the students into groups of 3. Give them 5 minutes to talk to eachother, tell eachother their interests. After the 5 minutes, each person has to introduce someone else from their group, including name, year, and icebreaker answer:
Icebreaker prompt: What’s a craft (broadly construed) you enjoy, now or as a kid? More specific the better. Maybe you like to crochet, maybe you used to doodle tighly wound spirals during math class, maybe you bend paper clips into funny shapes.
My answer: I sometimes fiddle with stick bombs! Then, I Make one on front of them and throw it at a wall.
Class discussion: What are math crafts?
Prompt discussion:
- what does “craft” mean, in the “arts and crafts” senes? How do you interact with it?
- What does math mean, how do you interact with it?
My thoughts are, math is the exploration of patterns emerging from rules and structures. What can I learn from my axioms? Once I have my objects, do they have properies I never defined? If so, we call it a theorem. Math crafts are crafts which are math. You build something following regular rules, and the shape and form of the object manifests. You don’t control the final form, only the method of construciton. Often, the final form has patterns you couldn’t have expected. Understanding those patterns is math.
For an example: Here is the Margaret Hunt Hill Bridge in Dallas Texas, desinged by Santiago Calatrava: (image from wikimedia)

Discuss:
- What are we even looking at?
- What shape is it? What parts speak to you?
- Important How was this designed? What rules does it follow? How would you make it?
- Why do the shapes follow form the design rules?
- What other patterns do you notice?
I want you to get in the habit of asking these questions, so we’re going to do more practice. We’ll learn how to be craft detectives
Craft detectives
Each table gets a mathematical craft that we will make later in the semester. They have 10 minutes to closely examine it, see how many patterns they can find, and answer the discussion questions above. Afterwards, each group will present to the class describing the craft, the rules it follows, and the patterns it makes. (I chose a good variety of things – hyperbolic crochet, pipe cleaner weaving, a hopf fibration, and a hyperbolic oragami piece).
Afterwards, give the students some time to mingle and look more closely at the objects from the other groups. Have it be a mini-show and tell. A person from the group can stay back, and tell other groups about it.
Then, bring the class together and do your own show and tell. Show off all the crafts for the coming semester, and say a bit about the math for each of them.
Flexagons
After the break, have the students apply their craft detective abilities. Can they repoduce a craft, using their observational detective skills?
First goal: Hexaflexagon Give each table strips of paper, tape, and a hexaflexagon. Task them with making their own. Here are a sequence of leading questions:
- Can you find the three sides? What is an easy way to go between sides?
- What basic shapes are the paper folded into? How many of them are there?
- How can you fold many of these shapes from a paper strip? Can you do it without using the preexisting hexagon?
- Try to assemble a triangled strip into the hexaflexagon.
Second goal: Hexahexaflexagons Next hand them a hexahexaflexagon, and ask them to make it. If students get stuck, try these hints:
- You can cut your sample apart to see, if very stuck
- What shapes are the samples made of? How do you make those shapes?
- How many triangles are in the hexaflexagon? The hexahexaflexagon?