Weaving Pipe Cleaners

Jan 2024
craft math-crafts-class

Summary:

Craft: weave pipe cleaners into mats. Discover how singularities in the weaving pattern forces the mat to curve in 3D.

Math: Examine how adding extra angle around a vertex produces negative curvature. See the shape the negative curvature imposes.

Weaving Pipe Cleaners

Summary

in the last couple of weeks, we learned how placing polygons together edge to edge can force 3-dimensional shapes – our first experience with curvature. Today we will apply this technique in a crafty way, in a much more expressive medium than regular polyhedra. We will weave together pipe cleaners, forcing curvature by introducing polygons in the weave with different number of sides. Using this, we can make a whole menagerie of fuzzy math critters.

a collection of woven pipe cleaners, popping into three dimensions

Materials and setup

Materials

Each student will need

  • around 25 pipe cleaners (they will need to reuse them)
  • Occasional access to scissors For a class of 20 students, you can get 1000 pipe cleaners for 20 dollars, and (optionally) a pack of ballons for the class.

pipe cleaners naturally come ordered in blocks of colors. For each table of 3, I put 3 seperate colors (around 20 each)


Artist:

Ruth Asawa. See more info here

Part 1: flat weaving

A weave is composed strands, following two simple rule:

Question 1: Make a weave of pipe cleaners with these underlying patterns. Are there multiple ways to weave these patterns?

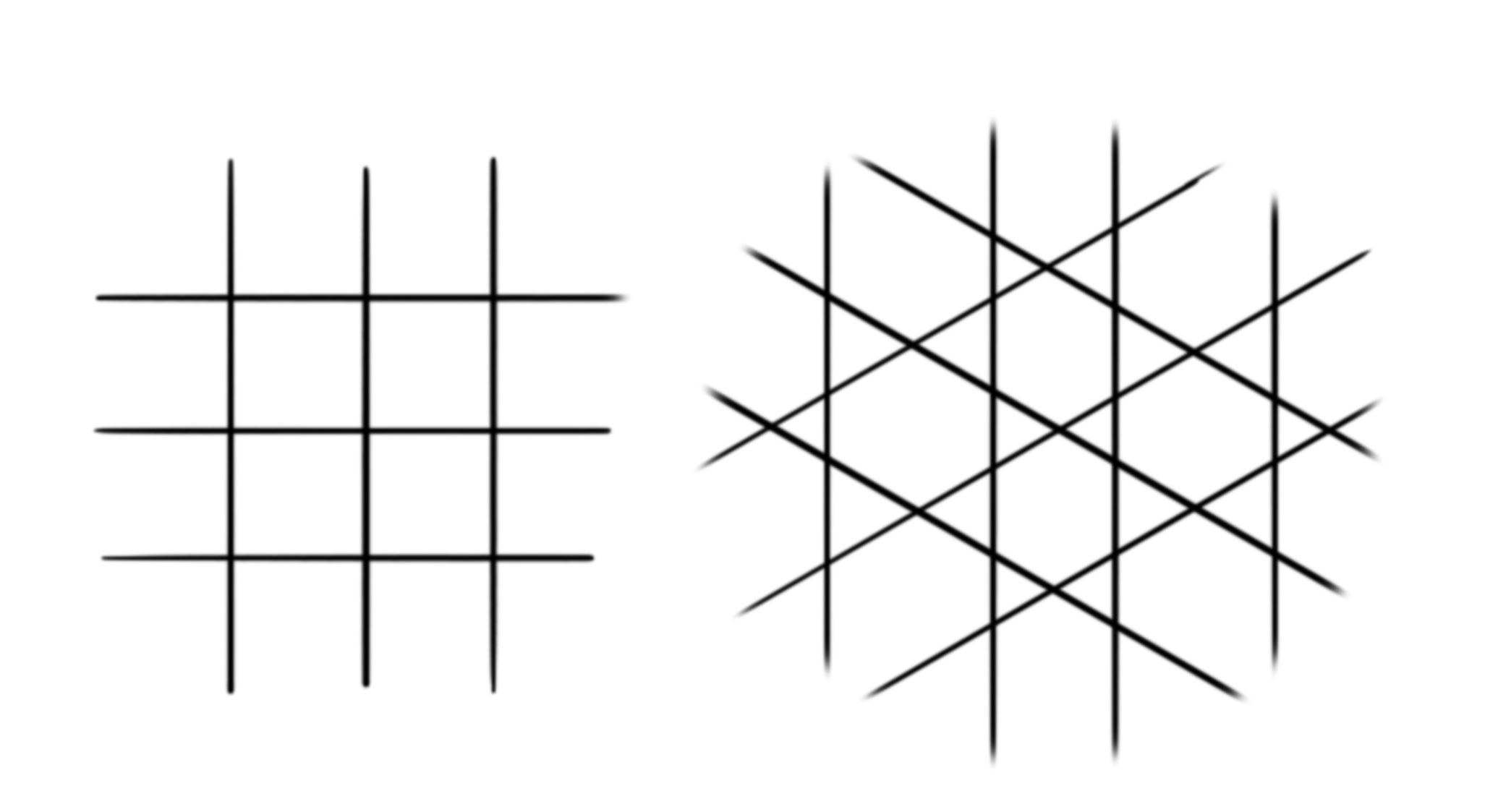
two models for weaving. On the left a square grid, on the right a set of 3 parralel lines which form hexagons and triangles.

Pedagogical note

The square weaving is easy for students. The hexagonal weave can be very difficult. It took almost an hour for everyone to get a proper hexagonal weave. Some common confusions

  • People started with a square grid, and tried to weave in the third set of lines. This is optimally bad and confusing.
    • To counter this, Start with the hexagon, and follow with the square grid
  • People thought that every pair of colors had to weave togehter, not following the rule that
    • To counter this, In your example weave, have one strand weave around multiple colors
  • People put three pipe cleaners at each vertex, instead of making little triangles
    • To counter this, Make the “only two crossings” a stated rule

Be liberal with hints – it can get frusterating. This part is the hardest of the activity.


Answer

The left one gives a standard weave

a square grid, woven out of pipe cleaners

The one on the right gives what’s called the Kagome Lattice

a woven hexagonal grid of pipe cleners. It forms 3 parralel lines which form hexagons and triangles.

This has three sets of parallel lines, here one for white, yellow and purple. The construction is quite easy to remember. White always goes above purple, purple always above yellow, and yellow always above white.

There is only one way to realize the square lattice. There are, however, two ways to make the kagome lattice. The pictured one is white > purple > yellow > white, but we could do white > yellow > purple > white. This would result in a mirror image lattice, which you cannot get by rotating or flipping the original lattice.


Question 2a: Examine each of the polygonal regions of the woven lattice. How do the crossings behave for the strands bordering the region? As you follow clockwise along the border, see which crossings are over and which are under. Try this with a few of the polygons. What do you notice? Can you explain what you see?

Answer

Going clockwise around each region, we see only over crossings or only under crossings, depending on the region. Here’s a pentagonal example: notice how every crossing is under.

a pentagonal weave

We call “over” and “under” the orientation of a region. Over regions necessarily border under regions. If we color the over regions red, and the under regions blue, we form a checkerboard pattern. Here, we see the coloring for the kagome lattice

kagome lattice over a piece of paper. Each hexagon is colored in red, each triangle colored in blue

Why is the orientation well defined? remember that every strand has to alternate over and under. Label the sides of the polygon as strands 1 through $n$. If strand 1 crosses over strand 2, then equivently strand 2 goes under strand 1. Therefore, the next crossing along the strand 2 must be over. So, strand 2 goes over strand 3. And so on: each strand crosses over the next. If instead strand 1 went under strand 2, then each strand would cross under the next. Either way all crossings in a region must be the same type.

This also explains the altrenating orientation of adjacent polygons. We define the orientation based on overness/underness while going clockwise. A crossing that looks “over” from one polygon, looks “under” from the adjacent polygon.


Think of each woven polygon like a staircase. As you move around the region clockwise (always turn right!), we have to step “up” or “down” to get to the next pipe cleaner. Each polygon is a very funky staircase: You start at one point, only walk upstairs or downstairs, and end up at the same place. We’ll call the two types of polygons “upstairs” and “downstairs” polygons. Similar “impossible figures”, like the staircase we described, influenced the work of artists like M. C. Escher, see below. Notice how traveling the oppisite direction turns an upstairs into a downstairs polygon – we must always be moving clockwise!

Question 2b: (optional, but cool) . Place your woven lattice over a piece of paper. Mark the centers of one of the upstairs regions types in red, and the downstairs regions in blue. Connect two dots if their region is of the same type, and they share a corner. What are you drawing? how do the two colors relate to one another?

Answer

Here is the construction for the kagome lattice:

A trianglular grid of red dots, with blue dots in the center of each triangle. The blue dots are connected in a hexagonal grid.

The positive regions (the hexagons) form a triangular lattice. The negative regions (the triangles) form a hexagonal lattice. In particular, these lattices are dual. Applied to the square lattice, we get two offset square lattices, again dual to one another.


In these simple weaving patterns, the positive regions and negative regions are everywhere the same shape. We can classify these regular woven patterns using two numbers, the number of sides of the upstairs regions and the number of sides of the downstairs regions. For the square weave, both upstairs and downstairs are squares, so we write the weaving pattern as  □↗□↘. The kagome lattice has 3 sided and six sided regions, so the pattern is △↗⬡↘ or ⬡↗△↘, depending on which is upstairs and which is downstairs. (these two weaves are mirror images of one another). These should remind you of the three ways to tile a plane with equilateral tiles:

Part 2: curved weaving

The last couple of weeks, we experimented with putting too many or too few polygons around each vertex. This forced things to curve in the third dimension. Let’s try the same trick here.

Question 3: make a woven pattern with all (geometically) squares but exactly one triangle. Can you make it so it continues infinitly, still with only one triangle?

Answer and pedagogical notes

Introduce the question by asking for four sided things, instead of specifically squares. Students will make something that looks like this

Insert picture of flat triangle thing

Insist that they continue out for two layers, like above. Say something like, “Are you sure you can keep this going without adding more triangles?”

Next follow up with “Those don’t look like squares! those look like rectanges! Can you rearrange them to be truely square?” This part is a good puzzle – to get everything to be even, things need to bend into the third dimension. Here’s the result:

Picture of bent triangle

If students are so inclined, challenge them to complete this into a cube, assembling 8 of these triangles together.

Picture of a cube


Question 4: Start with one of your flat lattices. Modify it by choosing one polygonal region, and adding or removing an edge. Explore – how does this relate to curvature? Here are some guiding questions:

Here are some suggestions:

Answer

square $\implies$ pentagon

This is an exploration question, so there are of course no complete answers. Instead, I’ll show you my own explorations. Starting with $\{4,4\}$

a square grid, woven out of pipe cleaners

I added a pentagon, giving this weave.

a square grid, woven out of pipe cleaners, with a pentagon in the center. The lines are straight, and it looks janky.

This made me add in a set of purple pipe cleaners. Notice how the added lines aren’t straight, and the squares no longer look quite so square. I rearranged things to look more regular, and got the following:

a square grid, woven out of pipe cleaners, with a pentagon in the center. It is more regular now.

This rearrangement forced things to curve away from the plane.

a square grid, woven out of pipe cleaners, with a pentagon in the center. Low angle picture, which bends slightly out of the plane

Adding only a single edge caused a fairly subtle curvature. We can get more extreme curvature if we add more edges.

hexagon $\implies$ nonagon

Materials: 12 pipe cleaners of each color, 36 total

Here is the result of replacing a hexagon in the kagome lattice with a nonagon. Notice how much more it curves! This is partially because $9/6 > 5/4$, and partially because I’ve added more layers to give the curve a chance.

pipe cleaner object. There are hexagons everywhere, except the very center, which has a nonagon

This one is nice because it admits a very pretty, consistent color scheme. Here’s the top down view, notice how each color is the same pattern, rotated by 60 degrees.

pipe cleaner object from top down

I think this is quite a pleasing little shape. It casts some great shadows:

pipe cleaner object, casting shadows

And works wonders as a hat

mischevious looking human wearing pipe cleaners as a hat


Part 3: Symmetric weaving

We’ve seen how local modifications of the waving lattice changes the overall shape. But what if we applied these modifications everywhere? Instead of just 1 pentagon, have all pentagons. This should let us weave curved lattices.

Question 4: Weave a $\{3,3\}$ lattice. Once you make the lattice, rearrange it so that each triangle is the same size. What shape do you get? How do you connect it with the $\{3,3\}$platonic solid

(Hint: try to weave it from circles in the plane)

Answer

It turns out, you can do it with 3 circles in the plane:

three pipe cleaners, bent into circles, arranged like a venn diagram and woven togehter.t

I can’t resist mentioning that this configuration of loops is called the borromean rings. Though no two circles are linked, the three are attached together. Notice how every inside part has 3 sides, so they are technically triangles. The entire outside region also has 3 sides, so it is another triangle. To see this, we rearrange the rings to be symmetric in 3D space

three pipe cleaners around a balloon, as the three equators

Here, I used a ballon to form the sphere inside the rings. I originally tried to weave the pipe cleaners along the ballon as a base, but it was kind of a mess. With the balloon, we can see that the circles act like lines, but on a sphere.

Let’s relate this to the $\{3,3\}$ platonic solid, the tetrahedron. We use the same trick as the planar weaves. we label the triangular regions on the sphere as positive or negative according to the over/underness of the weave. Placing a vertex at the center of each positive region, and connecting the positive regions which share a vertex using an edge, we build a solid. We can similarly connect the negative faces, and get another tetrahedron. This is because the tetrahedron is self-dual.


Bonus question: Weave the other 2 pairs of platonic solids: The $\{3,4\}$ and $\{3,5\}$ lattice.

Answer

Here are models of the $\{3,4\}$ and $\{3,5\}$ weaves:

two pipe cleaner spheres, one with a balloon in it

Let me tell you step-by-step how to make the $\{3,5\}$ weave, which is the harder of the two. you can figure out the $\{3,4\}$ yourself :).

Materials: 6 pipe cleaners, optionally a balloon ### step 1 We start by building out the pentagon, and go from there. Since we want to build the weave into a sphere, we pre-curve each pipe cleaner into a circle. Arrange 5 of these pipe cleaners into a star, with the curve arranged so that the lines bow out from the center.

five near circle segments, arranged in a pentagram on the table

step 2

Next we add the 6th (and final) pipe cleaner, encircling the central star. Weave this in place, and connect the ends together.

same arrangement, but now with an encircling ring around the pentagram

step 3

Now we finish up the planar weave. Connect each pipe cleaner to itself, making sure you follow the weaving rules (always alternate!).

Pentagram arrangement of circles, with a sixth encircling circle

step 4

If you count carefully, we’ve already achieved the $\{5,3\}$ weave. It doesn’t much look like it, because the outer ring of pentagons is extremely distorted. To make them all even, expand the inner pentagon, while pushing it upwards in the plane relative to its enclosing circle. Here’s the halfway picture:

the pipe cleaners form a dome on the table, with a small pentagram on top

And here’s the final sphere:

now its a sphere! made out of 6 equators, arranged like a pentagram! wowsers

Here’s a model with the orientations labeled, using the balloon trick as before.

Now the icosohedron is full of a baloon.

Math discussion

Notice how the pentagons have positive orientation, while the triangles have negative orientation. Connect the centers of the pentagons together, and you get a dodecahedron (the $\{5,3\}$ solid). Connect the centers of the triangles, and get an icosahedron (the $\{3,5\}$ solid). The polyhedra with edges given by the pipe cleaners is called the icosidodecahedron

The resulting critter is lots of fun to play with. You can wrap and unwrap it lots of different ways, by expanding and contracting some of the pentagons. For example, expand the top and bottom pentagons, and you get a lovely bracelet.


Question 5: Weave a hyperbolic lattice, like the $\{3,7\}$ or $\{5,4\}$ weave. How does the result compare to the flat weave with a single singularity you constructed in question 4?

Some remarks:

Guide for weaving hyperbolic lattices

Here are step-by-step instructions for making a $\{7,3\}$ lattice.

Materials: Scissors, 32 pipe cleaners. Along the way, you will cut the pipe cleaners as:

  • 7 full length pipe cleaners (layer 1)
  • 14 half-length pipe cleaners (layer 2)
  • 54 1/3 length pipe cleaners (layer 3) ### step 1: Layer 1 We start by making the first heptagon. If we tried to make the heptagon out of straight pipe cleaners, we would get some unwanted intersections. To help us out, we should pre-bend the 7 layer 1 pipe cleaners.

Next, weave them into the heptagon. Continue the weaving to the seven triangles attached to the border of the heptagon, Make sure to have the lines bend outwards, to remove unwanted intersections. (I didn’t do the triangles in this picture). With this, we have finished the first layer.

Step 2: Layer 2

This parts somewhat more involved. Start weaving in the third layer, with the 1/3rd lenght pipe cleaners. I used 3 alternating colors for the last layer. Heres a sample:

Step 2: Layer 3

This part is somewhat more involved. Start weaving in the third layer, with the 1/3rd lenght pipe cleaners. I used 3 alternating colors for the last layer. Heres a sample:

We want to attach the pipe cleaners as we go, ensuring the lattice doesn’t unwind. Whenever we have a triangle formed on the outer layer (for example, with the pink and blue above), twist the ends together. I always chose my twist direction using the weaving rules. Some of these outer strands will cross 4 other strands before ending (the blue), while others will only cross 2 (the white on the left side). For those that cross 2, I cut the 1/3 length into 1/6 before twisting the ends. Here’s a picture of my little mitts doing some twisting!

Keep going at it, and you’ll eventually finish the third layer. This part took me about an hour.

Step 4: tightening

If all is well, you should have constructed an honest to god hyperbolic lattice! But, it probably looks a little janky. Too flat in the middle, to bunched up on the outside, with unevenly sized heptagons in the middle. We can fix this by tightening up the layer 1 stands. We started with them long to make it easier to work with, but we don’t need to work with it anymore! For each layer 1 strand, unwind one end and pull.

As you pull, make sure to rearrange the crossings to avoid bunching. Tighten all the strands by an equal amount, whatever length looks good to you. Rearrange things to make each heptagon regular and equal sized. Here’s what I got as a result. All thats left now is to trim off the excess.

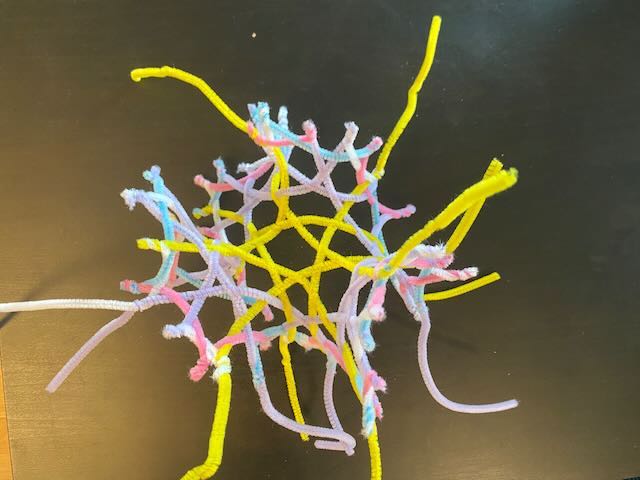
Math discussion

Here’s the final product:

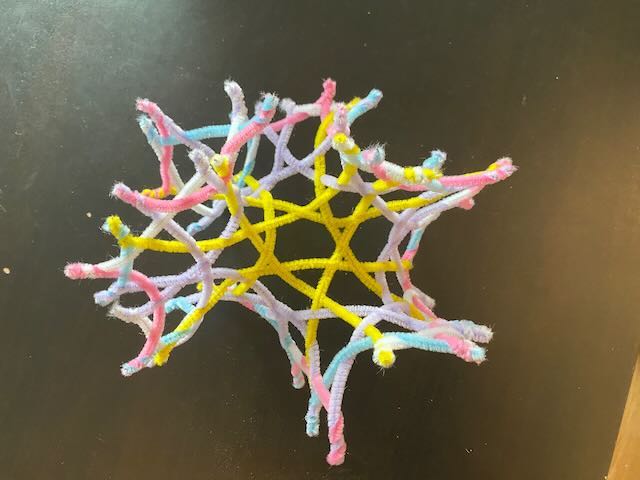
Notice how different the flurls look, compared to the localized change we did before (left versus right object). The localized addition of an edge caused localized curvature. While this made the entire surface pop into 3D, it still locally looks flat. In contrast, the $\{7,3\}$ weave just keeps curling, bit by bit, everywhere on the surface. Each new layer introduces new flurls. You can imagine how dense and wrapped up the fourth layer would have to be. A negatively curved object in 3 dimensional space quickly becomes unmanageable.

This construction taught us more morals about hyperbolic space. One is the extreme tedium of step three, an evergreen problem with negatively curved crafts. Hyperbolic space is really big. Each new layer requires exponentially more strands, and hence exponentially more work. With weaving, 2 layers is too few to see much interesting, and 3 layers already is a sizable project. It’s a tough world.

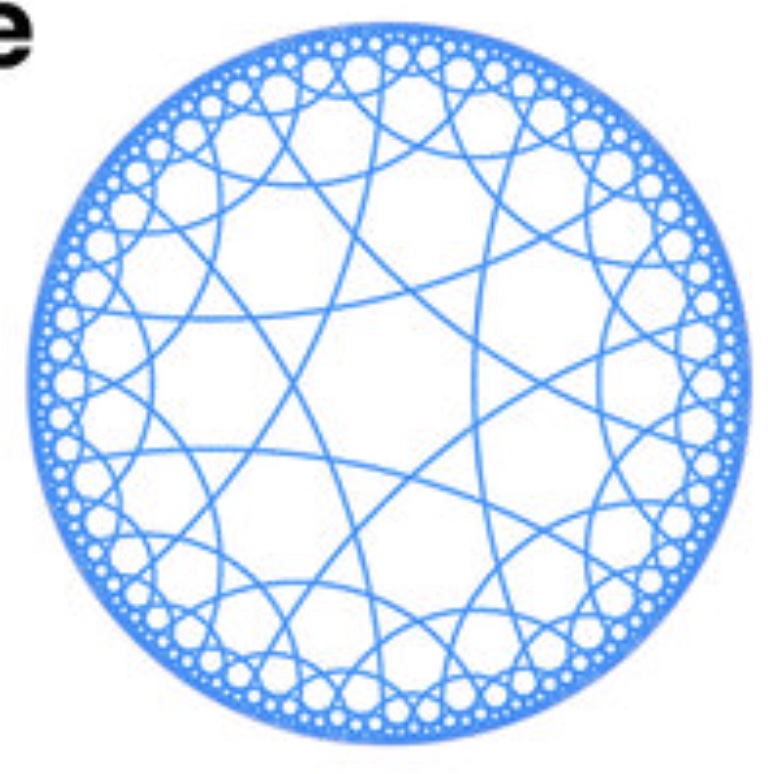
Curved weaving becomes exciting when the pipe cleaners pop out of the plane. In this experiment, the transition happens between layers 2 and 3. Back in step 2, to fit the lattice in the plane, we needed the pipe cleaners to curve. The second layer needed to curve more strongly. Compare the picture in section 2 with a picture of the $\{7,3\}$ kagome lattice (Also called a Triheptagonal tiling) in the hyperbolic plane. In the picture below, the lattice is drawn in the Poincare disc representation of he hyperbolic plane (from Hyperbolic lattices in circuit quantum electrodynamics ). This shows a universal truth, that we can fit a hyperbolic object on a disc if we squish and squash the outer parts the right amount.