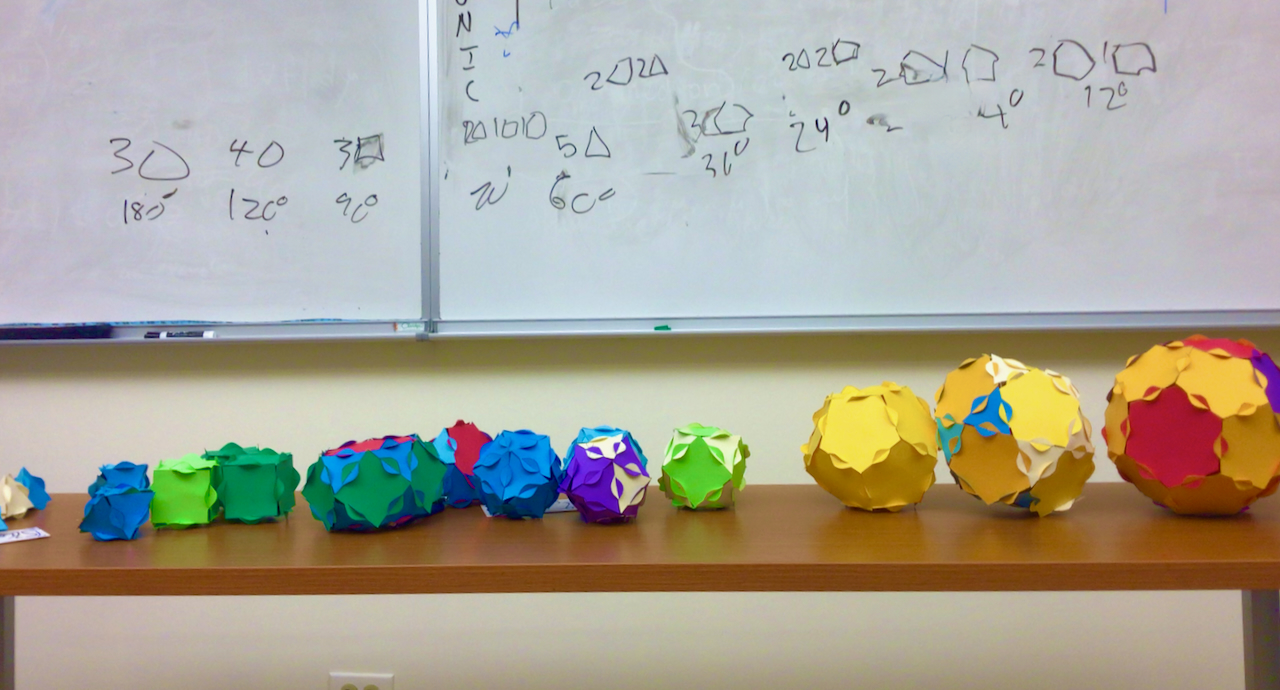Interlocking Paper Polyhedra

Jan 2024
craft math-crafts-class

Summary:

Craft: cut out slide-together polygons out of construction paper. Assemble these into polyhedra!

Math: Discover the platonic solids, and the rules governing what faces can fit together to make convex polyhedra. Study the angular defect around each vertex.

Interlocking Paper Polyhedra

Summary

Welcome to math crafts! Today, we will follow the footsteps of the greeks before, and discover the platonic solids. Cutting paper into polygons and attaching them together, we can make a 3D object! The object’s shape is controlled by the number of polygons around each vertex – our first encounter with curvature. Just like the mathematicians of old, you won’t know the answers ahead of time. Instead, I’ll suggest questions for you to ask, and your explorations and curiosity will lead you ahead. You might not answer the original question, but you will understand something along the way.

all platonic solids in a cluster

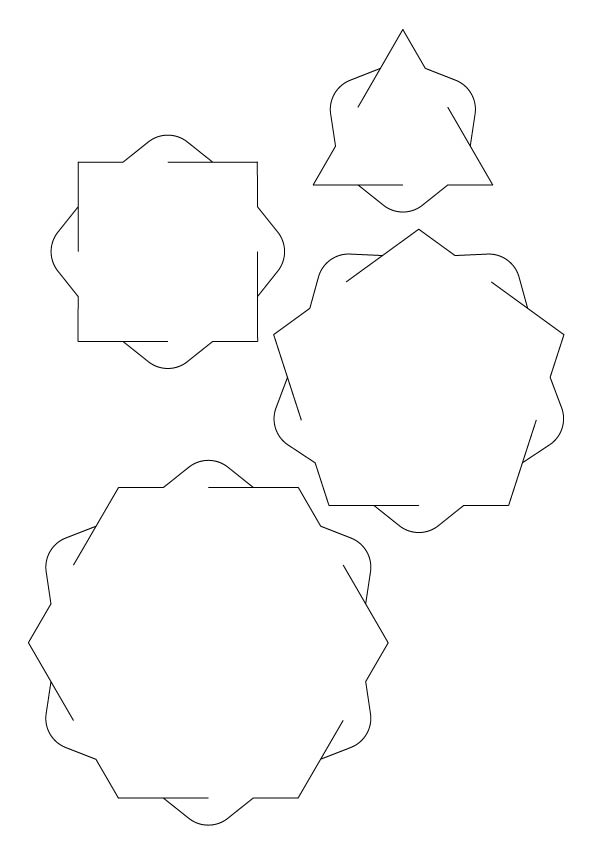
To make easy-to-attach polygons without tape or glue, we use interlocking paper tabs. I make some templates (see below), highly inspired by itsPhun. If you want heavy-duty plastic versions of these interlocking polygons, you can buy some there.

template of 4 different polygons, each with tabs

Materials and setup

Materials

Each table of 3 students will need:

  • 16 sheets of 65lb cardstock (details below)
  • 3 Scissors

It will be good to have on hand for the class:

  • a protractor or two
  • tape

Setup

We will have the students cut out the paper polygons using the templates below, which look like the picture above. Precision is important, specifically for the cut that ends halfway through the tab. Cutting through a stack of papers with scissors and a template gives rather unsatisfying, shoddy results. With a little prepreperation, things go more smoothly. We will use a trick inspired by George hart. Place a template above a stack of construction paper or cardstock, all atop a scrap piece of cardboard or two. Then, hammer a nail through all the layers at essential points of the template: The endpoint of the slit (Important to get this precise!).

Awl hammered through a paper template, stack of construction paper, and a cardboard backing

This has a few benefits: The nail holes hold the paper aligned together. This makes it easy to hand out whole stacks of paper, and lets the students cut the whole stack at once. They just need to cut to the holes, helping their percision. Also, the scraggly nail holes hold the tabs together quite well. Compare the build quality below: Left is without nails, right is with nails.

comparison of build qualiy. Left, without pre-nailing verticies, is shoddy. Right, with the pre-nailing, is much better.

I organize my students into tables of 3. For each table, make:

  • 1 2-hexagon template
  • 1 4-pentagon template
  • 1 8-square template
  • 1 12-triangle template

Place each of these over a stack of 4 sheets of cardstock. Ideally keep all of each shape the same color across the class. I used 65 lb cardstock, which has a good heft with some longevity. If you only have construction paper or lower weight stuff, it should still work, but will be more flimsy. I’d be cautious about heavier cardstock: 4 sheets was already pushing the limit for the cheap class scissors. With heavier stock, you need less per stack if you want clean cuts.

In total, I had 4 groups. This came out to

  • 64 sheets of cardstock paper
  • 4 of each template

This comes out to 380 total punches. This took me about 1-1.5 hours– it goes by quick once you get a rhythm.

Templates

Here are the templates. Printed on US-standard *1/2 - 11 paper, these give polygons with edge length 1.5 inches. These are oriented for right handed cutting convenience, if you’re left handed its convenient to flip the template.

If you’d like to edit these templates or laser cut them or something, here’s the vector file:


Platonic solids

Today we will make some balls. Like soccer balls. These are made by sewing together white hexagons with black pentagons, and inflating. We will do the same, using interlocking paper instead of sewen leather. Demonstrate by creating the tetrahedron on front of them)

For us to talk about these questions together, we need a common language for 3D shapes. Today we’re only going to think about shapes made of flat sheets attached together. These are called Polyhedra. The flat parts of the polyhedra are called faces. Each of these is a 2 dimensional shape (a polygon). The boundary of each face is a collection of one dimensional line segments called edges, and the corners of each face are points called vertices.

diagram labeling edges, faces, and verticies

Understanding check: How many faces, edges, and vertices does a cube have? (pictured above)

Answer

6 faces, 12 edges, 8 verticies


We make two groupd rules:

  1. All faces the same

    Each face must be a regular polygon, and you’re only allowed one type of polygon.

  2. Each vertex has same composition

    The faces around each vertex must be the same. For example, the tetrahedron has 3 triangles around every single vertex. This keeps our balls symmetric

Pedagogical note -- introducing the problem

  • Frame this as a conversation with the whole class. Have people identify the number of faces, veticies, and edges of the tetrahedron you made, and show them how to count it.
  • The only thing I wrote on the board is the two ground rules.
    • The wording of the second rule is important. I wrote “same number of faces at each vertex”, and it confused people when it came to archemedian solids later. They would make shapes where some verticies were two pentagon one hexagon, and others two hexagon one pentagon.


Question 1: Build as many platonic solids as you can think of. Once your table makes a solid, have someone write its name on your table’s whiteboard. How many could you find? How many faces does each have?

Pedagogical note -- running platonic solid activity

Cutting the paper took about 40 minutes, and groups tended to finish all platonic solids around 75 minutes in. They were already talking about the questions below during the construction time, so the tasks overlapped.

After handing out the paper, students get very in the cutting mindset and thought they had to cut everything out before trying to make anything. Have them resist the temptation, maybe pass out too few templates at the start, and have them ask for more when they need it. Another optimization is to force the students to cut out the polygons in stacks. If you print polygons on each paper (like i did), then students will tend to seperate them and cut them paper by paper. One way to avoid this is to not print anything on the cardstock, and only use a printed paper template on top. Then, people are forced to cut through the whole stack.


Answer

We need to know:

  1. the number of sides of each face
  2. the number of faces around each vertex

We go through case by case: 3 triangles per vertex: This results in a 4-sided pyramid known as a tetrahedron

paper model of tetrahedron

4 triangles per vertex: This results in the 8-sided octahedron

paper model of octahedron

5 triangles per vertex: This results in the 20-sided icosahedron

paper model of icosahedron

3 squares per vertex: This results in a cube, sometimes also called the hexahedron. It is 6-sided.

paper model of cube

3 pentagons per vertex: This results in a 12-sided shape called the dodecahedron

paper model of dodecahedron


Question 2: I have another name for the octahedron: I call it the $\{3,4\}$-hedron. Likewise, I call the tetrahedron a $\{3,3\}$-hedron. Can you guess what a $\{p,q\}$-hedron means? Can you name all your other polyhedra?

As mathematicians, once we discover something, we need to give it a name – how else can we discuss it with one another? Come up with names for the platonic solids you’ve made. Try to make it so someone who just knows the name could figure out how to build the shape. (if you already know names for these shapes, can you come up with better names?)

Pedagogical note

The goal of this question is to get students to realize all the polyhedra are made from a uniform procedure.

Not all groups need to get to this, but at least one should. Have them write their naming scheme (some version of the Schläfli symbol) next to the standard names on the board. When you synthesize the class at the end, use group to explin the Schläfli symbol.


Answer

You can make up many names, but here’s what math history has decided on. To build a platonic solid, we only need to know:

  1. the number of sides of each face
  2. the number of faces around each vertex

So our name needs to describe these two numbers. Lets say the number of sides on the face is $p$, and the number of faces around the vertex is $q$. Then, we write the associated platonic solid as $\{p,q\}$. This is called the Schläfli symbol of the solid. It doesn’t look much like a name, but it is very good at distinguishing different solids like any good name-tag.

Of course, these shapes also have names with letters in them. See the table below. The names come from greek, indicating the number of faces for each solid. The number of faces does uniquely describe each object among platonic solids, but gives no indication of how to build it.

sides on each face faces on each vertex Schläfli symbol Number of faces Common name
3 3 $\{3,3\}$ 4 Tetrahedron
3 4 $\{4,3\}$ 6 Cube (Hexahedron)
4 3 $\{3,4\}$ 8 Octahedron
5 3 $\{5,3\}$ 12 Dodecahedron
3 5 $\{3,5\}$ 20 Icosahedron


Question 3: Are there any other platonic solids you haven’t built? Can you prove there are no more?

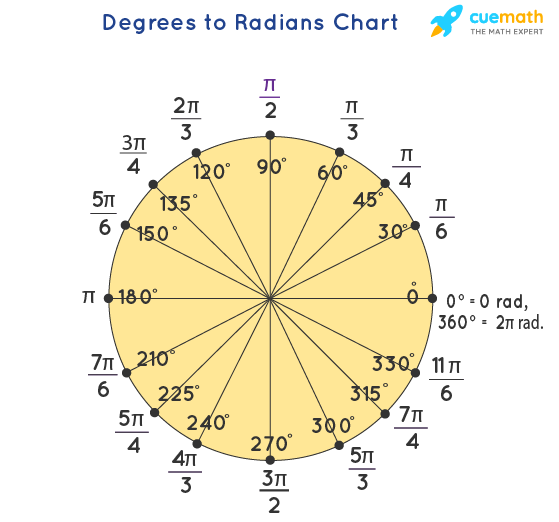
Hint: Think about the angles around each vertex. Here are the angles for each regular polygon, measured in radians. There are a total of $2 \pi$ radians in a circle.

number of sides angle
3 $\pi/3$
4 $\pi/2$
5 $3\pi/5$
6 $2\pi/3$
$\vdots$ $\vdots$

Pedagogical note

My students knew the interior angles for each polygon already in degrees, except the pentagon. All my groups thought the pentagon should have 72 degrees, when it has 108. This was quickly fixed by handing them a protractor. The activity works even if you don’t give them radians. If you want to give radians, draw this chart on the board

diagram of radians vs degrees

And include the information of the table by drawing the 5 polygons, and labeling their interoir angles.


Answer

First we try to make polyhedra out of only triangles. How many triangles can we fit around each vertex? We saw we could make 3,4, and 5. If we try to put 6 triangles around, the total angle around the vertex is $2 \pi$. So, the triangles stay flat in the plane, and the triangles never closes up into a sphere. A similar thing happens for 7 or more triangles.

We see from the triangle case that we can’t form a sphere unless the total angle around a vertex is less than $2 \pi$. Let’s apply this to squares now! Using the angle chart, we can fit at most 3 squares around each vertex (which gives a cube), and no more. For pentagons, we can fit at most 3. For hexagons, we can fit only 2, which gives a degenerate polyhedra. This continues for all higher angles.

Therefore, the only platonic solids are those constructed above.


Question 4: You should have found a platonic solid with 5 triangles around each vertex. What happens if you put 6 around a vertex? 7? (you might want to cut off the tabs and use tape for 7 or more).

Likewise, what happens when you put 4 squares around a vertex? 5?

Can you determine a rule which relates the behavior of a vertex to the angles of the faces surrounding it?

Answer

First we try to make polyhedra out of only triangles. How many triangles can we fit around each vertex? We saw we could make 3,4, and 5. If we try to put 6 triangles around, the total angle around the vertex is $2 \pi$. So, the triangles stay flat in the plane, and the triangles never closes up into a sphere. A similar thing happens for 7 or more triangles.

We see from the triangle case that we can’t form a sphere unless the total angle around a vertex is less than $2 \pi$. Let’s apply this to squares now! Using the angle chart, we can fit at most 3 squares around each vertex (which gives a cube), and no more. For pentagons, we can fit at most 3. For hexagons, we can fit only 2, which gives a degenerate polyhedra. This continues for all higher angles.

Therefore, the only platonic solids are those constructed above.

There are three different behaviors depending on the sum of angles around the vertex.

  1. If the sum of angles is less than $2 \pi$, then the construction closes up and we get a platonic solid. We call this Spherical
  2. If the sum of angles is equal to $2 \pi$, then we get a tiling of flat space. This regiem is called Euclidean
  3. If the sum of angles is greater than $2 \pi$, then the vertex is still forced out of the plane, but in an unusual way. We will investigate this regieme more next week. We deem this hyperbolic

The behavior depends on the Schläfli symbol according to the following table, from a book by Robert Fathauer. Yellow is spherical, red is euclidean, and blue is hyperbolic.

table of spherical, euclidean, and hyperbolic regular tesselations


Question 5: Platonic solids are pretty restrictive, so let’s break some rules. What shapes can you make that follow rule 2, but not rule 1? That is, there are multiple types of faces, and each vertex is surrounded by the same combination (say, two triangles and two squares per vertex). These are called archemedian solids

Construct a few different archemedian solids. Calculate the angle defect (2 $\pi$ - total angle) around each vertex. Is it positive, negative, or zero?

Are there any archemedian solids with 3 different types of faces? 4?

Pedagogical note

This question takes as long as it needs to. Often people will want to break rule 1 before they’re even done with the plantonic solids, encourage them to do so. Try to encourage a variety of different shapes.

Make sure people think critically about actually following rule 2, often there are hidden verticies which breaks things.


Answer

There are many archemedian solids to make. Here is one called the cubeoctoahedron, where each vertex has 2 triangles and 2 squares, alternating as you move around the vertex. The total angle around the vertex is $5 \pi/3$.

paper model of a cuboctahedron

Here is a list of some shapes students made:

As well as some which aren’t archemedian solids:

  • A Stellated octahedron. Not a archemedian solid, but shows what happens when we break the “positive angle defect” rule. It has verticies with 8 triangles surrounding.
  • Pyrimids of various forms. These are Johnson solids
  • Something similar to the cuboctahedron, but the top and bottom squares are replaced by hexagons. Funnily enough, this isn’t on wikipedia’s list of johnson solids. I don’t think this is actually possible to make with rigid faces, but the paper is flexible enough to allow it.
  • Similarly, a dodecahedron with top and bottom face replaced with hexagons. Also not a rigid solid.
  • A monstrosity composed of the shape from above, divided in half like an ice cream sandwitch, and filled in with more hexagons. Also not a rigid solid.

Turns out, it’s surpisngly easy to lie to yourself and make something which isn’t a true solid.


Class activity

For the last 20-25 minutes: First, synthesize and give answers for all the questions above. When you talk about archemedian solids, hold up examples from the class and name them with math words (people like that). Explain how they are constructed, if you can. For example, the cuboctahedron is formed by cutting off the corners of the cube, and similarly for the icosidodecahedron. This got me some A-ha moments.

Then, designate one table as the display table. Have people calculate the angle defect for each of their polyhedra. Have them place it on the table, in order from largest to smallest, and write in dry erase marker on the table the schaflies symbol and the angle defect. Students should notice that the smaller the angle defect, the larger the shape. Explain how angle defect controls curvature, and the more tighly curved the sphere is, the smaller it must be. We will see more examples of this later in the course.

many paper polyhedra, all in line. They are sorted by angle defect, which happens to correspond to sorting by size