Uncertianty principles on Segal-Bargmann space

Oct 2025

talk

Summary:

The Fourier transform can be localized to encode the component frequencies of a signal at a particular time. This defines a function on a two dimensional “phase space”, with one dimension time and the other frequency. I will introduce my favorite phase space representation, the Segal-Bargmann transform, which takes a function on $L^2(\mathbb{R})$ and outputs a holomorphic function on $\mathbb{C}$. We will see how the phase space representation geometrically encodes the spectral properties of the original function, and build a dictionary between these two function spaces. Then, we manifest the uncertainty principle, stating that a holomorphic function in phase space cannot be too localized. First we will discuss coherent states, which have the largest possible $L^\infty$ norm for a fixed $L^2$ norm - a “minimal uncertainty” function. Then, we will prove a recent result of Nicola and Tilli, proving that the $L^2$ concentration of a holomorphic function on a set is maximized by coherent states on a ball.

Presented at:

• UC Berkeley student harmonic analysis, Fall 2025

🔗 Link to file

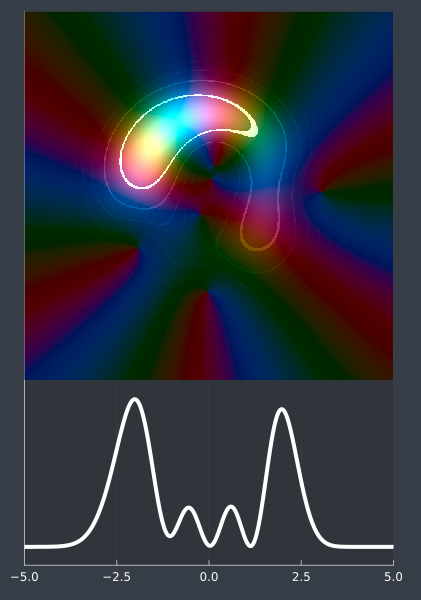
Let $P(z)$ be a polynomial on $\mathbb{C}$ with roots $z_1,\dots,z_n$. This is a vector in the Segal-Bargmann space, the space of holomorphic functions on $\mathbb{C}$, intersect the weighted $L^2$ space with gaussian weight $e^{-\mid z \mid^2}$. The $L^2$ density of such a polynomial is

We consider the region of $\mathbb{C}$ where the density is large, meaning it is within a factor of $e$ of the maximal value. Define the set

In my talk, I prove the following uncertainty principle:

Theorem: $\text{Area}(S_P)>= \text{Area}(S_1) = 2\pi$, with equality only when $P=1$.

That is, $\rho_P$ must be large on a large region. This shows that $\rho_P$ cannot be too concentrated in a small area, as then $S_P$ would be small. So, it is an uncertainty principle, showing that polynomials multiplied by a Gaussian must be sufficiently spread out.

Try it yourself:

Here is a plot of the set $S_P$ (the large filled-in area), for the polynomial defined by roots at the green dots. Try to get the set to be as small as possible.

• click and drag points to move zeros around.
• Double click to add/remove roots.

Each zero of $P$ is a local minimum of the function $\rho_P$. The stable manifolds of each zero (the set of points which flow toward that zero under the reverse gradient flow) all have the same area. This lets us decompose the plane into equal-area pieces. You can play with this here. Inducting this process into higher dimensions, we can split up any Kahler manifold into a full filling by equal symplectic balls. This is called the Biran decomposition. See my Talk on the Biran decomposition, and references therein.

Sources

I learned most of this from the very readable lecture notes Holomorphic Methods in Mathematical Physics, by Brian Hall.

The uncertainty principle I presented was proven in The Faber–Krahn inequality for the short-time Fourier transform by Fabio Nicola & Paolo Tilli. I presented the simplified proof present in A monotonicity theorem for subharmonic functions on manifolds, specialized to the Segal-Bargmann case. It took some work to extract my proof from these in the literature, cutting out all the chaff needed to generalize it properly.