Four skew lines at christmas time
Summary:
I made some ruled surface christmas ornaments. One ornament contains four skew lines, and comes with a riddle: Can you find a fifth line intersecting all the other lines? How many such lines are there? In this post, I prove that the number of lines passing through four skew lines is 0,1,2 or infinity.
I made a mathematical Christmas ornament, which holds a riddle.
The four-line riddle
Inside there are four strings. Can you line up the bauble so that the four strings seem to meet at a point in your vision? If you can, you have found a line which skewers all four skew lines. How many such lines can you find? My bauble has two solutions:
Solution 1
Solution 2
Play along at home:
You might find configurations of lines with no solutions to my riddle. You might get configurations with exactly two solutions (Remember, looking down the same line from opposite directions doesn’t count as separate solutions). If you’re very lucky, you could get only one solution, or infinitely many. But never 3, or 5, or any other number. This is a classic result from algebraic geometry. Let me state it more precisely.
Theorem
Let $\ell_0,\ell_1,\ell_2,\ell_3$ be four lines in three dimensional space $\mathbb{R}^3$. There are are either less than two lines $L$ which intersect all four other lines, or infinitely many such lines.
Let me sketch a proof. The key idea is to first consider the lines $L_t$ which pass through three lines $\ell_0,\ell_1$ and $\ell_2$, then see if any of the lines $L_t$ intersect $\ell_4$. We will see that the set of lines $L_t$ trace out a quadrtdic surface. Any line intersects a quadratic surface at most twice (or infinitely many times), and there you go. In detail:
Proof
Fix three skew lines $\ell_0,\ell_1,\ell_2$. We will show that there is a unique line $L_t$ passing through each of $\ell_1,\ell_2$ and a point $t \in \ell_0$. In particular, the space of lines passing through all three skew lines is one-parameter. To construct this line $L_t$, Form the plane $P_{1,t}$ passing through $t$ and $\ell_1$, and similarly $P_{2,t}$ thru $t$ and $\ell_2$. The intersection of these two planes is a line
\[P_1(t) \cap P_2(t) = L_t\]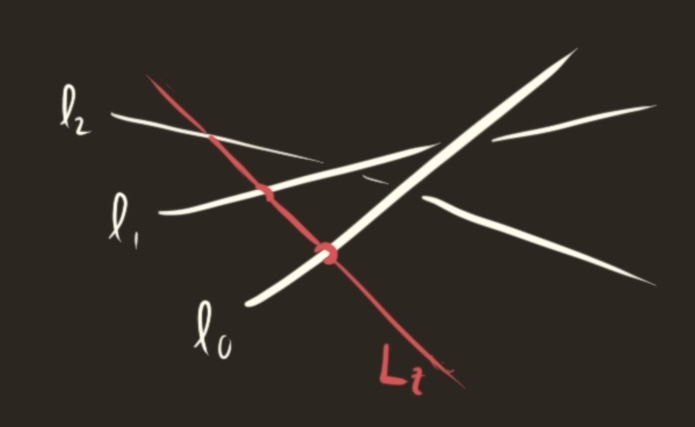
A line through three skew lines
By construction, $L_t$ passes throguh $t\in \ell_0$, and intersects $\ell_1$ and $\ell_2$. Define the locus of points on some line $L_t$ by $R$:
\[R = \bigsqcup_{t\in \ell_0} L_t\]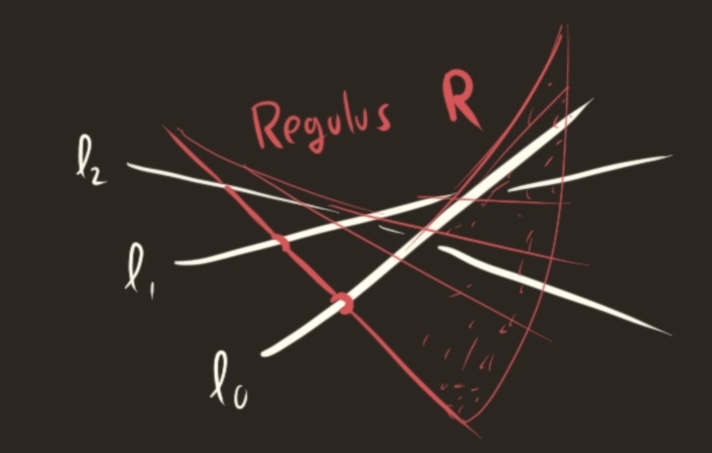
The lines $L_t$ trace out the regulus $R$.
All reguli are planes, hyperbolic paraboloids, or hyperboloids. This is an origami model hyperbolic paraboloids
This traces out a surface, known in the old tongue as a Regulus. The regulus $R$ is by construction a ruled surface, meaning it is traced out by lines $L_t$. Interestingly, $R$ is doubly ruled. It can be decomposed as a family of lines in two different ways. One way uses $L_t$, and the other uses an infinite family containing $\ell_0,\ell_1,\ell_2$. All we will need is the fact that $R$ contains all of $\ell_0,\ell_1$ and $\ell_2$.
Now fix a fourth line $l_3$, skew to $\ell_0,\ell_1,\ell_2$. Suppose there is an intersection point $p$ between $\ell_3$ and $R$. Then, $p$ is contained on $\ell_3$, and on some line $L_t$. This line $L_t$ intersects all of $l_0,l_1,l_2,l_3$. Thus, each intersection point $R\cap \ell_3$ contribute a line intersecting each of the 4 skew lines. (A priori, we don’t know that distinct intersections contribute different lines). We will prove there are at most 2 intersection points $R\cap \ell_3$, hence at most 2 lines skewering all 4 skew lines.
The intersection of $\ell_3$ with the regulus $R$ defines lines intersecting all four $\ell_0,\ell_1,\ell_2,\ell_3$
To control the number of intersections with $R$, we seek a polynomial $f:\mathbb{R}^3 \to \mathbb{R}$ which vanishes along $R$. Then the degree of the polynomial $f$ controls the number of times that any line can intersect $R$. Indeed, linearly parametrize $\ell_3$ as $\ell_3(s)$. Then, a point of intersection $p$ between $\ell_3$ and $R$ is a root of $f(\ell_3(s))$. If $f$ is quadratic, then $f(\ell_3(s))$ is degree 2 in $s$. This limits the number of roots (and thus the number of intersections) to $0,1,2$ or $\infty$. Hence, we seek a quadradic $f$ vanishing on $R$. First we construct a quadratic $f$ vanishing on $\ell_0,\ell_1,\ell_2$, then we will show it vanishes on all $R$. Here is a useful fact for our back pocket.
Lemma
If a degree 2 polynomial $f$ vanishes on 3 points on a line $\ell$, then $f$ vanishes on all of $\ell$.
Proof: Under a linear parametrization, $f(\ell(t)): \mathbb{R} \to \mathbb{R} $ is a degree 2 polynomial. By assumption, this function has 3 zeros. Any quadratic function on $\mathbb{R}$ with 3 zeros must identically vanish. QED
Next we construct the function $f$. For $f$ to vanish on all of $R$, it must certainly vanish on each of the lines $\ell_0,\ell_1,\ell_2$. In the following lemma, we construct a quadratic vanishing on these three lines.
Lemma
There exists a quadratic $f:\mathbb{R}^3\to \mathbb{R}$ vanishing simultaneously on any three lines $\ell_0,\ell_1,\ell_2$.
Proof: Fix 3 points per line, $p_{i,j}\in \ell_i$. If $f$ vanishes on each line, then $f(p_{i,j})=0$ for all $i,j$. We prove this by dimension counting. Denote the vector space of quadratic functions on $\mathbb{R}^3$ by $\mathcal{H}$. This space is ten dimensional, spanned by the functions
\[x^2,y^2,z^2,xy,yz,zx,z,y,z,1\]For every function $f\in \mathcal{H}$, we can evaluate at the specified points $p_{i,j}$, defining a linear map
\[ev: \mathcal{H} \to \mathbb{R}^9 \qquad ev(f) = \{f(p_{i,j})\}\]This is a map from a 10 dimensional space to a nine dimensional space. Because we’re decreasing the dimension by one, at least one dimension has to be squeezed to zero, and $ev$ must have a zero (More formally, this is the rank-nullity theorem). That is, there is always a quadratic $f$ vanishing on all nine points. By the lemma above, this $f$ vanishes identically on $\ell_0,\ell_1, \text{ and } \ell_2$.
With a little more fussing, we can show that if the lines $l_0,l_1,l_2$ are skew, then the images of each monomial under $ev$ are all linearly independent. That is, the map $ev$ is full rank, so the null space is always dimension 1. When the lines are skew, the choice of $f$ is unique up to scaling. QED
With $f$ in hand, we prove that $f$ vanishes on the entire regulus $R$.
Lemma
For a regulus $R$ generated by 3 skew lines $\ell_0,\ell_1,\ell_2$, There is a quadratic $f$ such that $f(x)=0$ for every point $x \in R$.
Proof: Construct the quadratic $f$ vanishing on $\ell_0,\ell_1,\ell_2$. Pull $f$ back along any one of the ruling lines $L_t$. Because $L_t$ intersects each of $\ell_0,\ell_2,\ell_2$, the function $f$ vanishes on 3 points along $L_t$. By the first lemma, $f$ vanishes on the entirety of the ruling line $L_t$. Hence $f$ vanishes on the entire Regulus $R$. QED
All together, we have constructed a nonzero quadratic function $f$ vanishing on the Regulus $R$. Along the fourth line $\ell_3$, $f$ has either 0,1,2 roots, or it vanishes identically and has $\infty$ roots. So, the number of intersection points between $\ell_3$ and the regulus $R$, which equals the number of lines $L$ passing through $\ell_0,\ell_1,\ell_2$ and $\ell_3$, is $0,1,2$ or $\infty$. QED
With a little more fussing, we can show that the defining function $f$ is unique up to scaling, if the lines $\ell_0,\ell_1,\ell_2$ are skew. This is true generically, so an arbitrary collection of lines will with probability one all be skew. We can also prove that $f^{-1}(0)=R$. But we need not worry if we only need the upper bound.
There can be issues where the intersection between lines happens off “at infinity”. Even though two parallel lines never cross, if we include points at infinity, we can say they intersect at infinity. This amounts to working in projective space. Here the statements are cleaner, because we don’t have to wring our hands about lines being parallel.
There are also configurations of lines with no solutions. We can arrange this by first choosing three lines $\ell_0,\ell_1,\ell_2$ and generating their regulus. Then, we can arrange for the fourth to not hit the regulus. No intersections with the regulus, no answers to my riddle.
A configuration of lines with no solutions. The blue lines $\ell_0,\ell_1,\ell_2$ generate the orange regulus. This has a big hole in the middle. If the fourth line $\ell_3$ passes through that hole, then it does not intersect the regulus and my riddle has no solutions.
The culprit for these counterexamples are 1 dimensional quadratic functions which have no roots. So, we can fix the problem by working in a world where quadratic functions always have roots: The complex plane. The best setting for these incidence problems is complex, projective three space $\mathbb{CP}^3$. The statement is now beautifully simple:
Theorem
Let $\ell_0,\ell_1,\ell_2,\ell_3$ be four lines in $\mathbb{CP}^3$ which do not all lie in a quadratic surface. Then, there are Exactly 2 lines $L$ which intersect all four other lines.
Remark: Because we solved the problem in $\mathbb{R}^3$ entirely using properties of polynomial functions, the proof carries over to $\mathbb{CP}^3$ without change.
The moral, if there is any, is that its surprisingly annoying to make sculptures of incidence geometry results. Unlike our platonic realm $\mathbb{CP}^3$, the real world $\mathbb{R}^3$ kinda sucks. I probably made 3 or 4 prototypes before I got a bauble which actually has 2 solutions, there’s way too many exceptions to the rules. Still, I’ll put up with all the annoyances of the real world if it lets me hang my theorems on a tree. Merry Christmas.
