⇤Math diary
Dec 28, 2023: Symplectic linear algebra and Gershgorin's circle theorem
Back on my lin alg kick. Eigenvalue juice poured directly down my throat. There’s many classical theorems about eigenvalues, and I want to find symplectic geometry perspectives on them. My eye currently lusts after Gershgorin’s circle theorem, which says eigenvalues must lie near the diagonal entries of a matrix.
Symplectic approach to linear algebra
Let me start by stating a classical theorem in linear algebra relating the diagonal entries of a matrix with its eigenvalues. This is the Schur-Horn theorem, which in fact spurred many developments in symplectic geometry:
Schur-horn theorem:
Let $M$ be an $N$ by $N$ hermitian matrix, with real eigenvalues $\lambda_1,\dots,\lambda_N$ and diagonal entries $d_1,\dots,d_N$. Then, the vector $\vec{d} = (d_1,\dots,d_N)$ lies in the convex hull of ${P_\sigma \vec{\lambda} | \sigma \in \Sigma_N}$, where $P_\sigma$ is the permutation matrix corresponding to an element $\sigma$ of the symmetric group on $N$ symbols $\Sigma_N$. In other words, the diagonal entries must be a convex combination of the reordered vector of eigenvalues. Conversely, for any vector $\vec{d}$ in the convex hull of ${P_\sigma \vec{\lambda}}$, there exists a hermitian matrix with eigenvalues $\vec{\lambda}$ and diagonal entries $\vec{d}$
There is a classical, purely linear algebraic proof due to (you guessed it) Schur and Horn. The modern perspective uses symplectic geometry of coadjoint orbits. We can parametrize all hermitian matrices with eigenvalues $\vec \lambda$ as the orbit of the diagonal matrix with entries $\vec{\lambda}$ under the conjugation action by $U(N)$. This is the coadjoint orbit of $U(N)$ on its dual lie algebra $\mathfrak{u}(N)^\ast$. Call this orbit $\mathcal{O}_{\vec{\lambda}} \subset \mathfrak{u} (N)^\ast$. The diagonal vector $\vec{d}$ is obtained by orthogonally projecting a matrix in $\mathfrak{u}(N)^\ast$ to the subspace of diagonal matrices. In Lie theory, this is called the dual Cartan subalgebra $\mathfrak{t}^\ast \subset \mathfrak{u}(N)^\ast$. The Schur-Horn theorem states that the image of $\mathcal{O}_{\vec \lambda}$ under orthogonal projection is the convex hull of ${P_\sigma \vec \lambda}$.
Atiyah and Guilleman-Sternberg gave a new proof using symplectic geometry. The coadjoint orbit $\mathcal{O}_{\vec \lambda}$ carries a natural symplectic structure, induced by the commutator of hermitian matrices. It also carries natural torus action, conjugation by the diagonal matrices $T \subset U(N)$. The torus action $T \curvearrowright \mathcal{O}_{\vec \lambda}$ is hamiltonian, meaning it is generated by the hamiltonian vector fields for some set of $N$ hamiltonian functions. The map sending a point on $\mathcal{O}_{\vec \lambda}$ to the values of the generating Hamiltonians is called the moment map. We denote the moment map $\mathcal{O}_{\vec \lambda} \to \mathfrak{t}^\ast$, identifying the hamiltonians naturally with the dual of the lie algebra of $T$. In fact, $\mu$ coincides with orthogonal projection to $\mathfrak{t}^*$! (This is a general property of moment maps on coadjoint orbits).
Now, the Atiyah-Guilleman-Sternberg convexity theorem states that the image of a moment map is the convex hull of the images of the fixed points of the torus action. In this setting, the fixed points are exactly the diagonal matrices, with entries $P_\sigma \vec \lambda$. These points are preserved by the moment map. So, the convexity theorem implies that $\mu(\mathcal{O}_{\vec \lambda})$ is the convex hull of ${P_\sigma \vec \lambda}$, which is exactly the Schur-Horn theorem. The moral is, convexity is more a general symplectic phenomena than a lie-theoretic phenomena.
In this same spirit, the symplectic geometry of coadjoint orbits has been exploited to solve other problems in linear algebra. The most prominent example is the Horn problem, which asks for a description of the eigenvalues of the sum of two hermitian matrices. For a description of this problem and its solution, see entry 25 of my diary.
Gershgorin’s circle theorem
Let me describe another result relating the diagonal entries of a matrix with the eigenvalues. We know that, for a diagonal matrix, the diagonal entries are the eigenvalues. we would guess that an approximately diagonal matrix has eigenvalues which are close to the diagonal. Can we quantify how close? The answer comes from an elegant 1931 theorem due to Gershgorin:
Gershgorin’s circle theorem
Let $A$ be an $N\times N$ complex matrix with entries $a_{ij}$. Define the Gershgorin radii by \(r_i(A) = \sum_{j\neq i}|a_{ij}|\)Define the Gershgorin discs $D_i \subset \mathbb{C}$ as a disc of radius $r_i(A)$ centered around the diagonal entry $a_{ii}$. Then, the spectrum $\sigma(A)$ is contained in the union of the gresgorin discs $\cup_{i} D_i$. That is, each eigenvalue is contained inside at least one of the discs.
The Greshgorin radii tells us how far the eigenvalues wander from the diagonal. It has a rather pretty visual description, if we draw the circles on the complex plane:
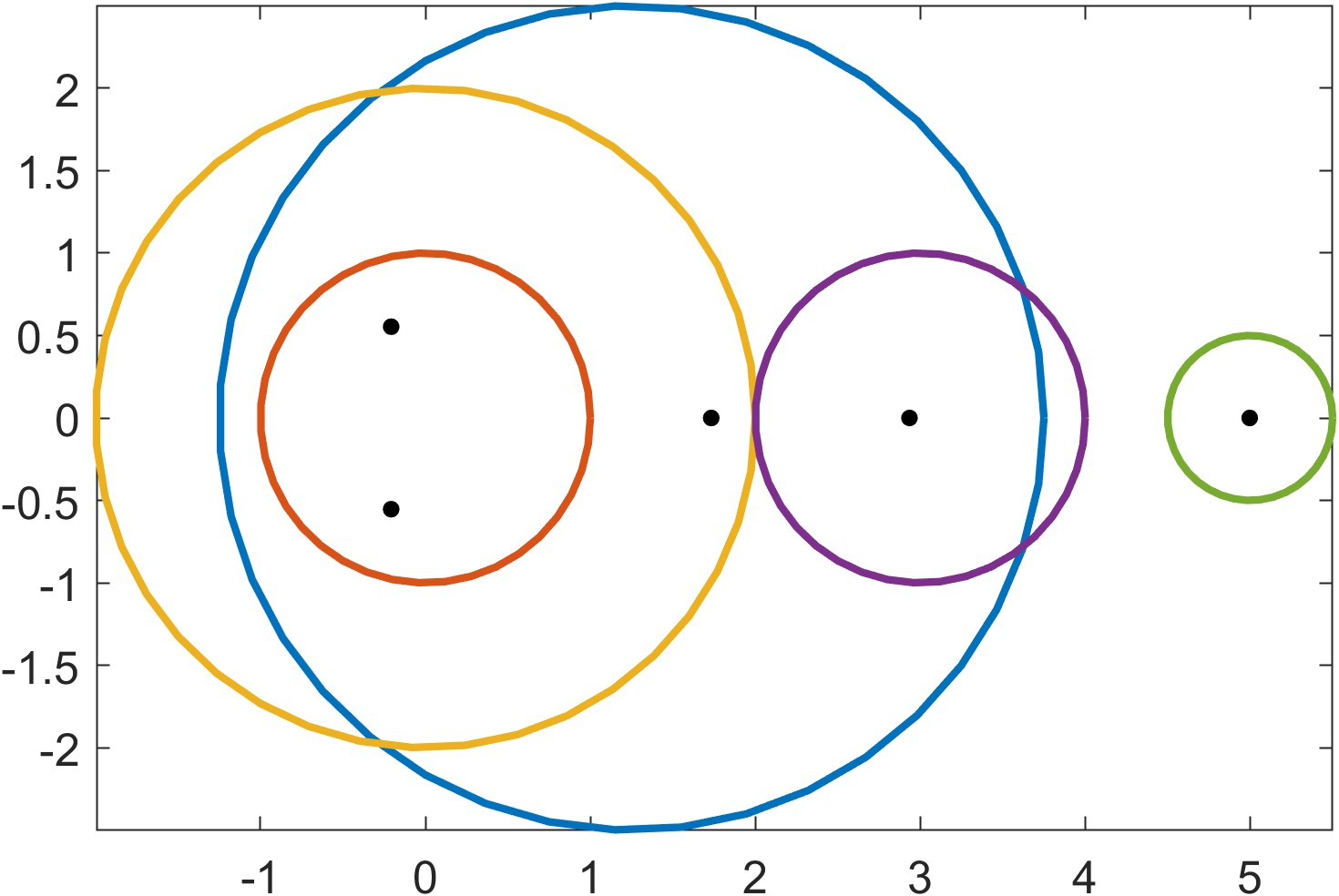
![[assets/images/geshgorin.png]] The proof is nearly effortless:
Proof of Gershgorin’s circle theorem
Say $\vec{x}$ is an eigenvector of $A$ with eigenvalue $\lambda$. The eigenvalue equation says \(\sum a_{ij} x_j = \lambda x_i\) Choose the entry $i$ such that $x_i$ has the largest absolute value (geometrically, we choose the axis which is closest to the vector $\vec{x}$). Then, we rearrange the equation: \(\sum_{i \neq j} a_{ij} x_j = (\lambda-a_{ii}) x_i \implies (\lambda-a_{ii})= \sum_{i \neq j} a_{ij} x_j /x_i\)Note that $|x_j|/|x_i|<1$ by construction. We apply the triangle inequality: \(|(\lambda-a_{ii})| = |\sum_{i \neq j} a_{ij} x_j/x_j | < \sum_{i \neq j} |a_{ij}| |x_j|/|x_j| < \sum_{i \neq j} |a_{ij}| = r_i(A)\)
Note that we don’t know which eigefnvalue is in which disc. The bound happens around whichever diagonal element is closest to the eigenvector corresponding to $\lambda$. With some more work, one can show that a disc which does not intersect any other disc must control its own eigenvalue.
I feel like I don’t understand this. The bounds make sense, but the circles are begging for a geometric origin. What can we say about eigenvalue geometry? More than this, I would hope. In fact, we can strengthen the circle theorem to fancier shapes, which tantalizes me so. This is due to Ostrowski (1937), and rediscovered by Brauer (1947):
Brauer’s ovals of cassini
For any eigenvalue $\lambda$ of $A$, there are a pair of indicies $i,j$ such that $\lambda\in K_{ij}(A)$, where $K_{ij}(A)$ is defined by \(K_{ij}(A) = \{z \in \mathbb{C} : |z-a_{ii}||z-a_{jj}|<r_i(A)r_j(A)\}\)The sets $K_{ij}(A)$ are called Brauer’s ovals of Cassini. Said differently, the spectrum $\sigma(A)$ is contained in the union of Brauer’s ovals of Cassini, $\sigma(A) \subset \cup_{i,j} K_{ij}(A)$
This is indeed a strengthening of gershgorin’s circle theorem, as $\cup_{i,j} K_{ij}(A) \subset \cup_i D_i(A)$. Now, we are bounding each eigenvalue according to its location relative to a pair of rows. The shape of each $K_{ij}(A)$ is goofy: Here are some level sets for different values of $r_i(A) r_j(A)$, where $a_{ii}$ and $a_{jj}$ are centered at the respective points:
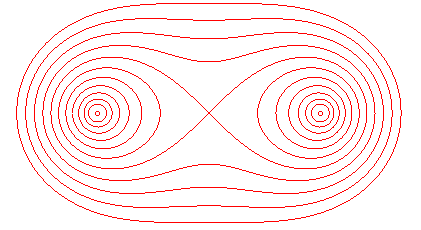
![[assets/images/ovals of cassini.png]]
Here’s an interactive toy to see Gershgorin’s circles and Brauer’s ovals of Cassini together: Link
What weird little shapes! why are they like that? what are they hiding? I feel like theres some geometry here that I’m not getting.
Symplectic Gershgorin’s circle theorem??
Both the Gershgorin circle theorem and the Schur-Horn theorem compare diagonal entries of a matrix to their eigenvalues. I want to try to incorporate them together. I wanna see the gershgorin circle coming from the toric structure of the coadjoint orbits. I wanna realize the ovals of cassini as toric slices of 2-tori. I’m mad with power.