Cursed geometry with a pointless compass

Sep 2025

blog talk fun

Summary:

A pointless compass is a compass without a center. It can only make circles of a fixed radius passing between two points. Can you construct a perfect hexagon with only a pointless compass? The pursuit of the pointless hexagon led me to a perversion of sacred geometry, where symmetry is broken yet shapes still manage to close up.

Presented at:

• Many cheerful facts, Fall 2025

I’ve never been impressed with sacred geometry (though I like this video). Take the central symbol of sacred geometry, the seed of life. The seed consists of seven overlapping circles with equal diameter, six equally spaced “petal circles” whose centers are placed on a central “source circle” (The names of the circles are my own).

The seed of life

The new age movement ascribed great spiritual significance to these seven little circles, for it is the start of all the sacred geometric constructions. the start of all things, each circle representing a day god toiled on the world. It appears across ancient temples for many different religions. To prove seed’s spiritual powers, they point to the miryad geometric constructions which start with the seed. Surely such geometric unity necessitates divine influence?

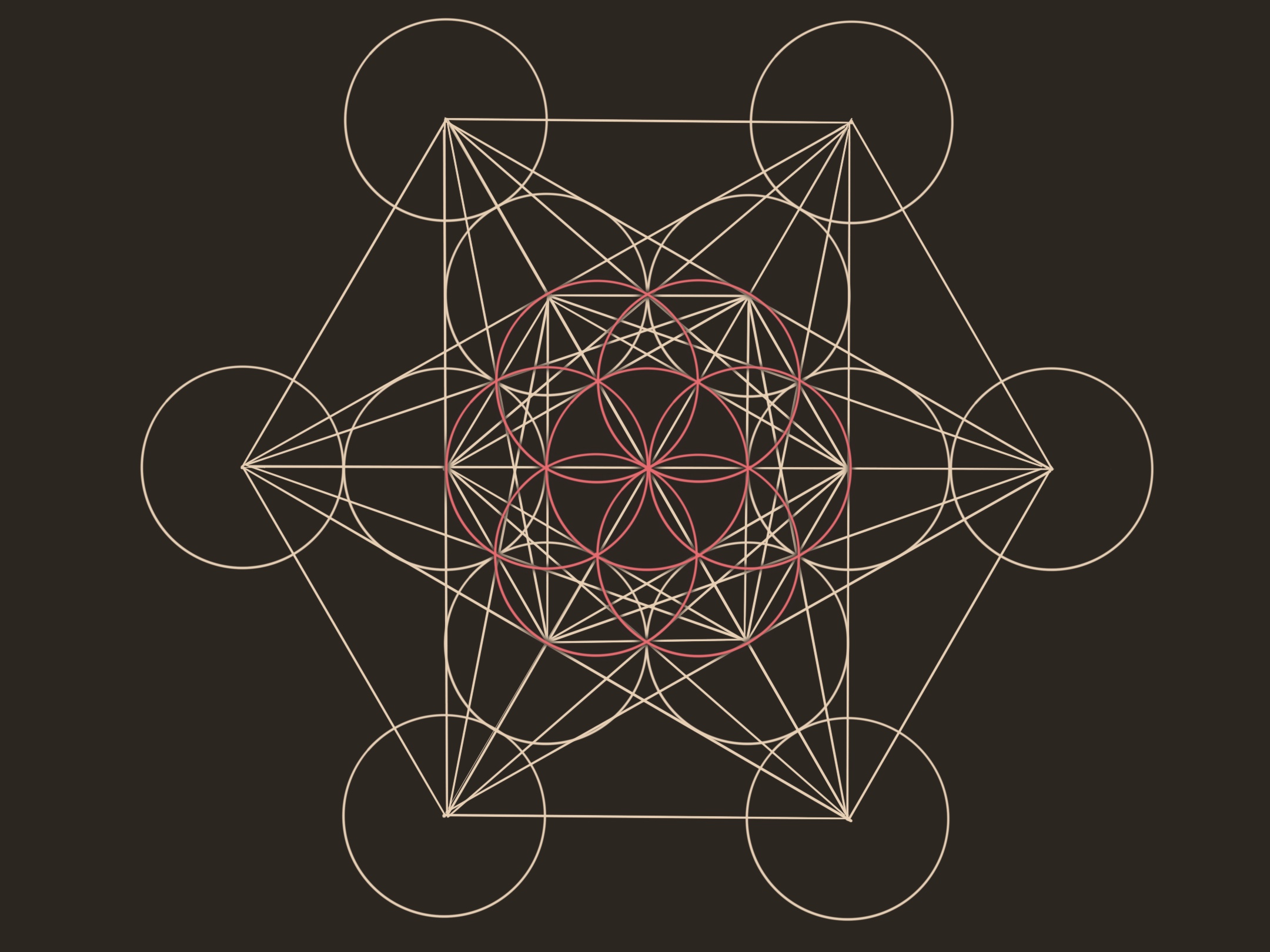
Metatron's cube

an arrangement containing the projection of every platonic solid onto the plane. The underlying seed of light is drawn in red. Funnily, the icosahedron and dodecahedron produced from metatrons cube aren't the projection in any perspective system I know. Its just a way of drawing something which looks like these shapes, using the lines from the cube. Be careful what you read on the internet. [This guy](https://www.youtube.com/watch?v=-vsESeNo1g0) is setting the record straight.

Or maybe not. I don’t find these constructions very surprising, much less evidence of a higher power. The flower of life, the progeny of the seed, is a hexagonal grid of circles! Starting with a construction of a regular grid, we can draw most anything. the sacred geometries are too symmetric, too perfect to be interesting.

A grid born from the seed of life

That being said, the seed of life makes a damn good hexagon. It’s the simplest way to construct a hexagon, which is probably why it appears on all those ancient temples. All you need is a compass. First, draw the source circle. Then, choose a point on the source circle and construct a circle of the same radius, the first petal circle. Construct the second petal circle, of the same radius, centered at the intersection of the first petal with the source circle. Chain this construction, and after six petals you will wrap back around to the start. The intersection of the six petals with the source circle forms a hexagon.

How to make the seed of life

I recently needed a regular hexagon, so I tried whipping up a seed of life. The issue is, my drawing program doesn’t let me draw circles with a fixed center. I can construct a circle passing through any three points, or a circle of fixed radius passing through two points. But I can’t get the center! I like to think of this setup as a compass without the central piviot point, a pointless compass. More familiarly, the only way I have to make circles is to trace the outline of something circular, like a glass. Can I still construct a hexagon? To formalize, Let’s fix the radius of the circle to one. Then,

Spoilers: The answer is yes. I recommend trying to find a construction before you read on, it’s a tricky puzzle (no tangencies allowed). I got a whole room full of grad students obsessing over this question.

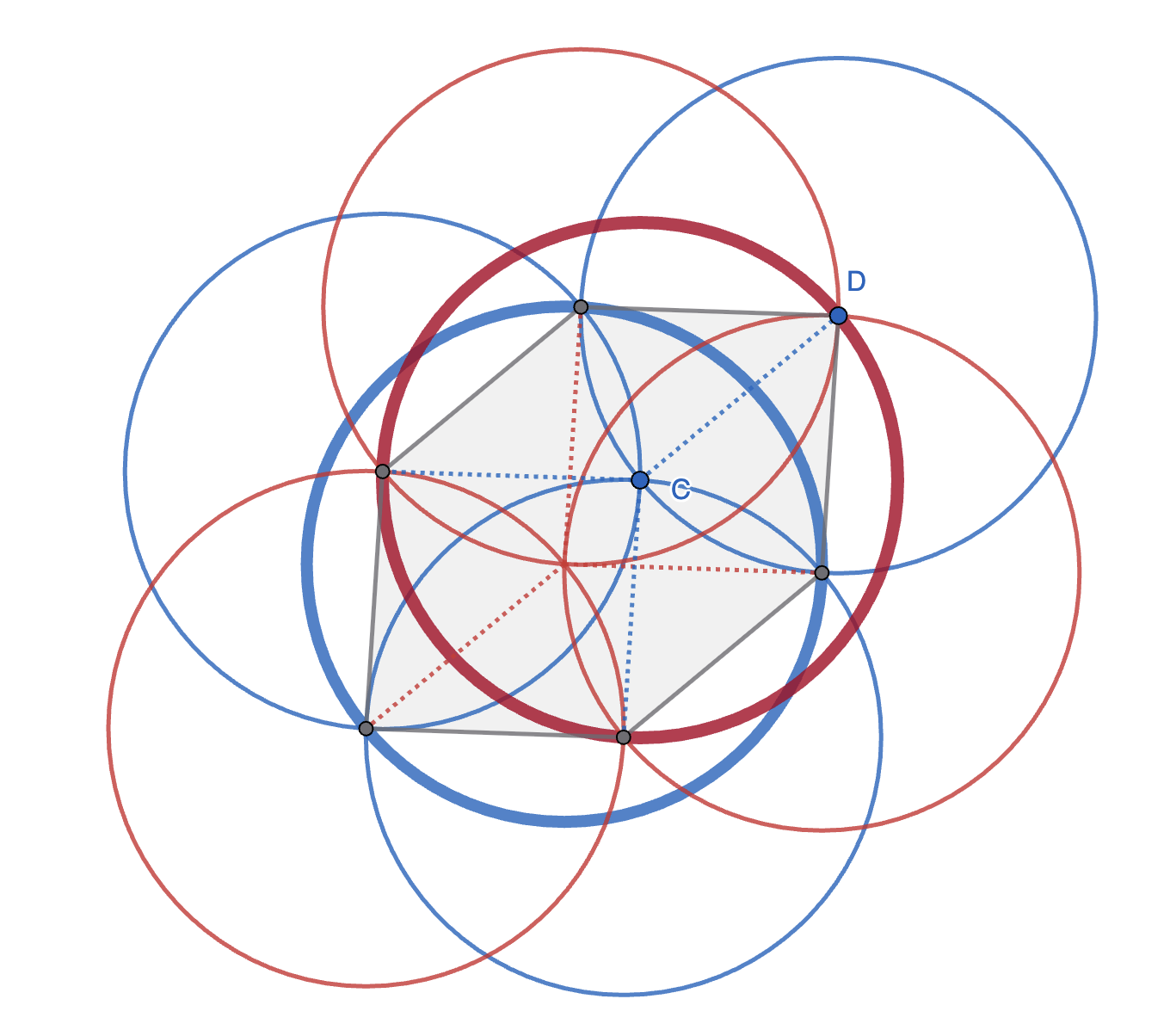
The only thing better then perfect is good enough. I drew the source circle, and eyeballed the center. I drew the first petal circle passing through the fiducial centerpoint. Next we construct a unit circle passing between both the guessed center point, and the intersection of the first petal with the source circle. There are two such unit circles, one already equal to the first petal. Draw the other option, the second petal. Finally, we repeat the process for the third petal circle.

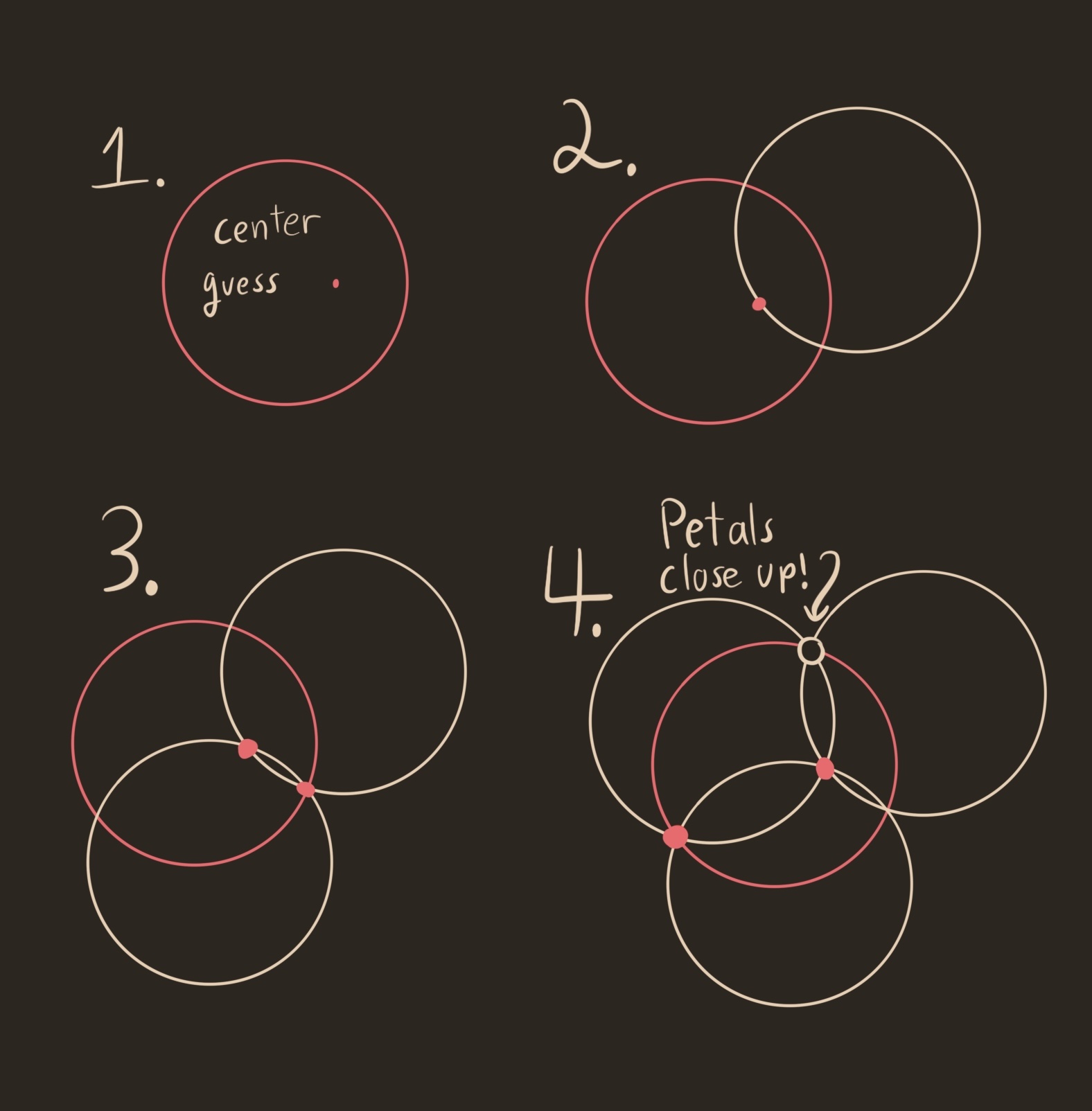
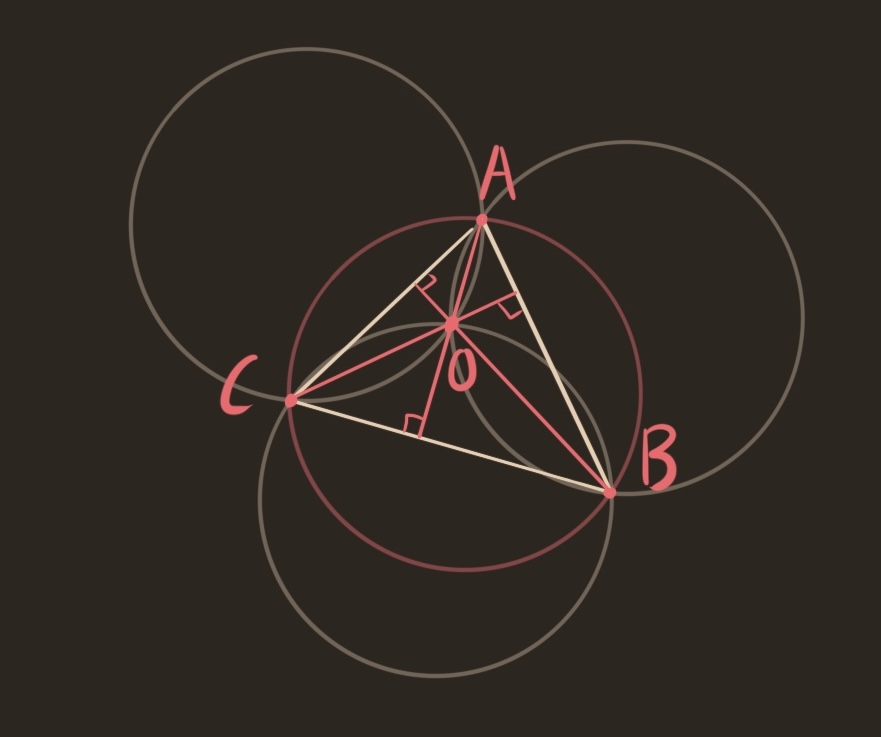
I was surprised to see the petals close up after only three circles. It looks like we got very lucky, that the unit circle through the guessed center and one petal intersection happens to hit the other petal intersection. But this always happens! Try it yourself! Point $A$ controls the source circle, point $C$ the guessed center point, and point $D$ the placement of the first petal circle.

To indulge myself, I’ll call this construction the contorted seed of life. If we got the center correct, then this would produce (half of) the original seed of life, and connecting the intersections of the petals with the source circle results in an equilateral triangle. For the contorted seed, we still get a triangle, but it is no longer equilateral.

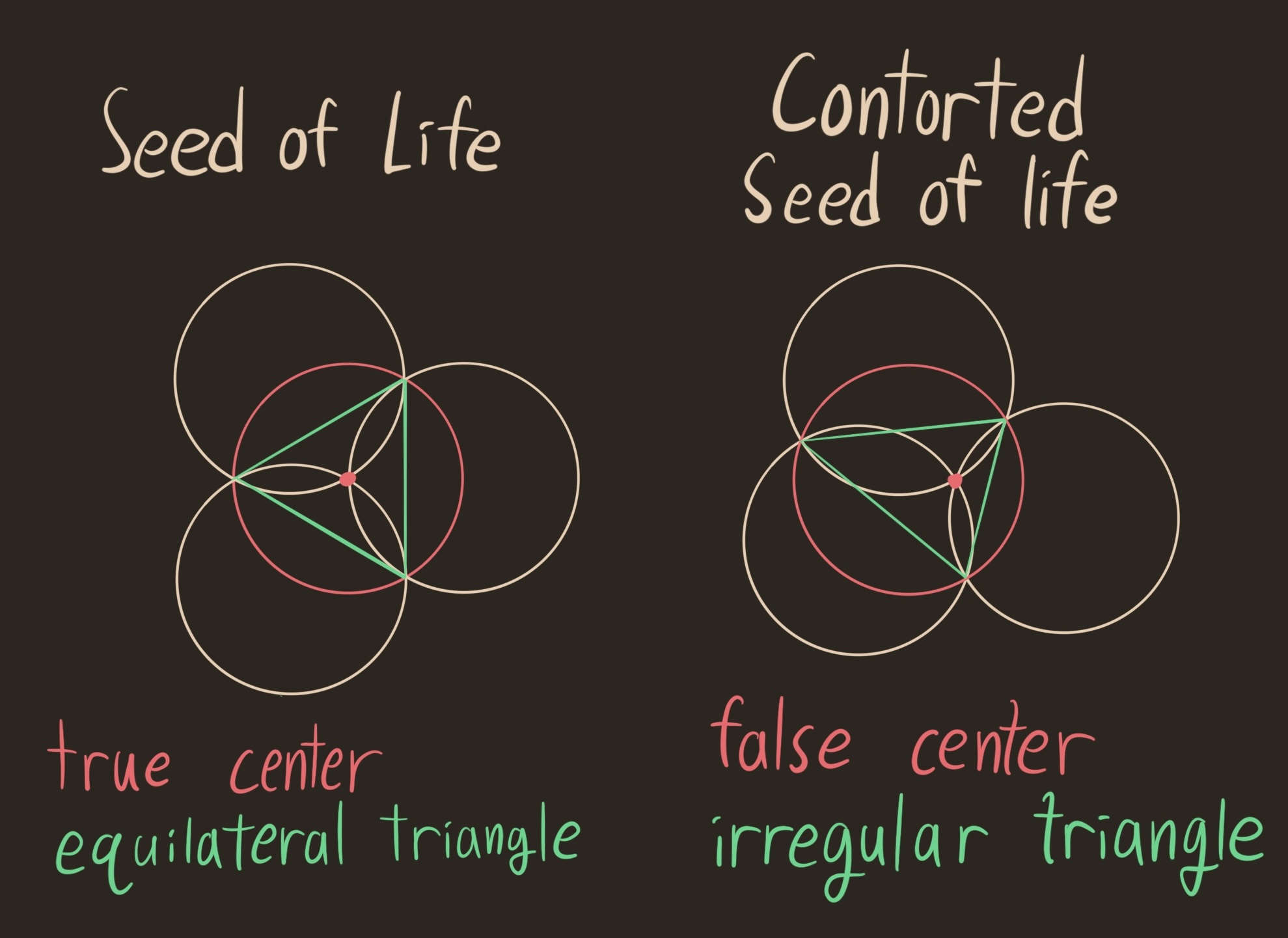
The contorted seed of life is the core of what I call cursed geometry. If we believe the symmetries of the seed of life are divine providence, then the non-symmetric contorted seed must be perverted. The geometric rigidity of the original is replaced with indecent flexibility in the contorted seed. Far from sacred geometry, the contorted seed is cursed. Yet, the petals close up. The flower still lives inside the seed. The contorted seed is blessed with a miracle, the emergence of geometric structure despite lacking any governing symmetry.

petals of the contorted seed

Now we explain the miracle, and prove that the petal circles close up like we saw above. First, let’s frame the problem more conveniently. We say that points $A,B,C$ are cocircular if there is a unit circle passing through $A,B,C$. The fact that the petals close up is equivalent to the following:

Theorem

Let $A,B,C,O$ be points. If $AOB, BOC$, and $COA$ are cocircular, then $ABC$ are cocircular.

---

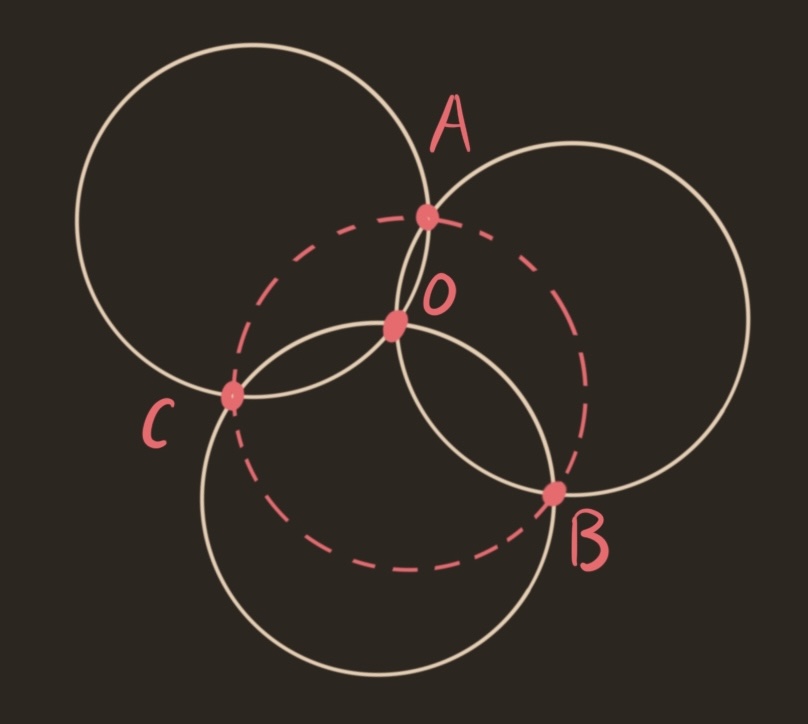
Proof: To attack this, let’s record everything we know: $A,B,C,O$ are all distance one from the centers of their respective circles. In the picture below, every pink line has length 1.

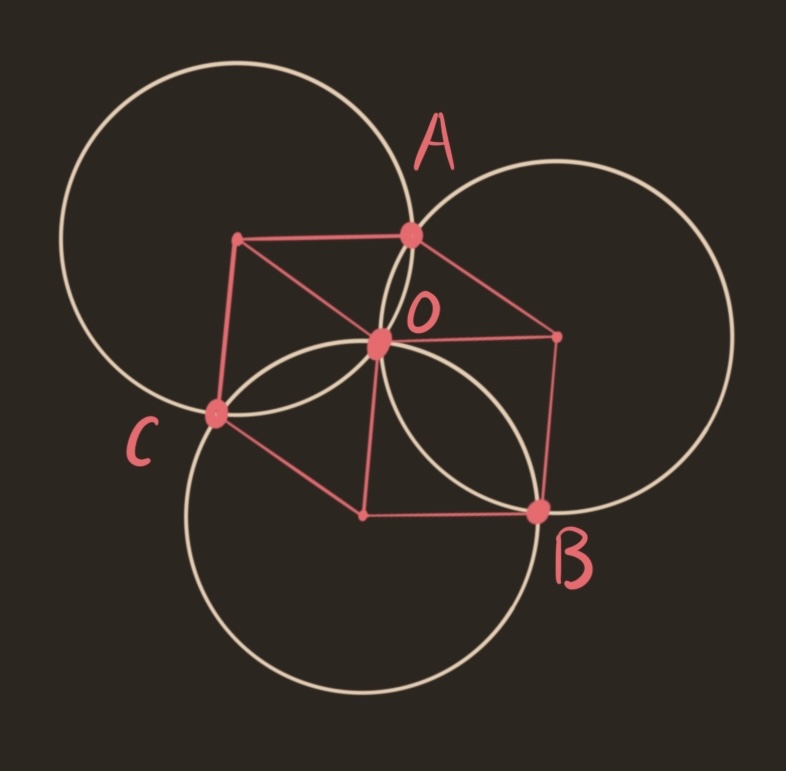
The shape formed by the radii look a whole lot like a cube, viewed corner-on. What if we include the back corner of the cube, as if drawing a wireframe? Since every edge in the cube is length one, each of the there quadrilaterals formed in the figure are in fact parallelograms. By the transitive property of parallel lines, the opposite edges of the hexagon must be parallel. So, the opposite angles must also be equal. Therefore, we can translate the bottom right parallelogram to nestle into the top left corner. This is like drawing the back right square in the wireframe cube. Repeating this for the other two corners, we construct the figure below. The new edges produced from this construction are parallel to the sides of the hexagon, so are forced to have unit length.

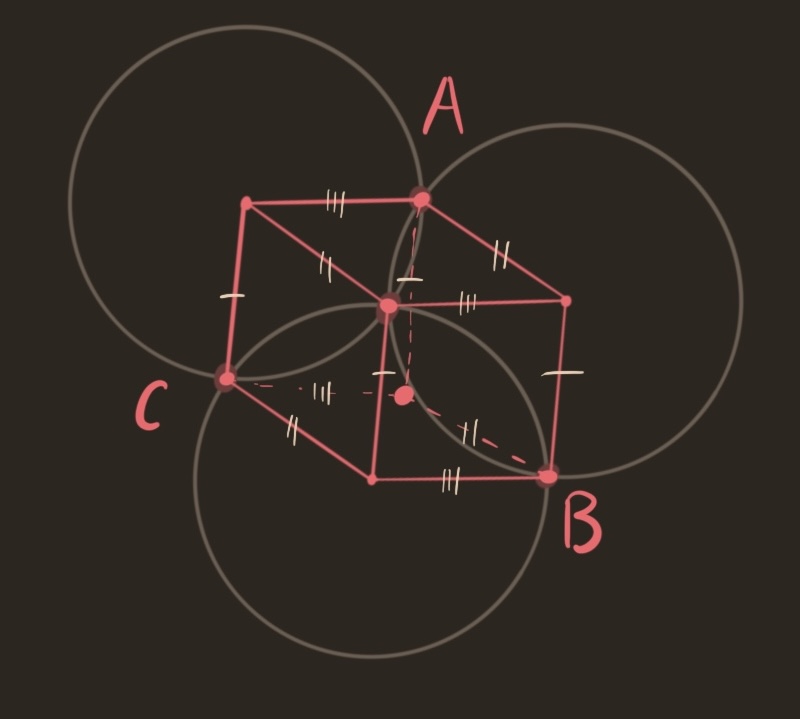
$A,B,C$ are all distance 1 from the same point, the back corner of the cube. Therefore, they must all lie on the same unit circle. QED.

The key to the proof was the insight that the we can swap the central vertex of the cube from the front to the back. While the front vertex is unit distance to the centers of the petal circles, the back vertex is unit distance to $A,B,C$. This suggests a duality between the intersection points of the petal circles $A,B,C$ and the centers of the petal circles. If we temporarily forego the pointless compass with a pointed one, we can construct unit circles centered at $A,B,C$.

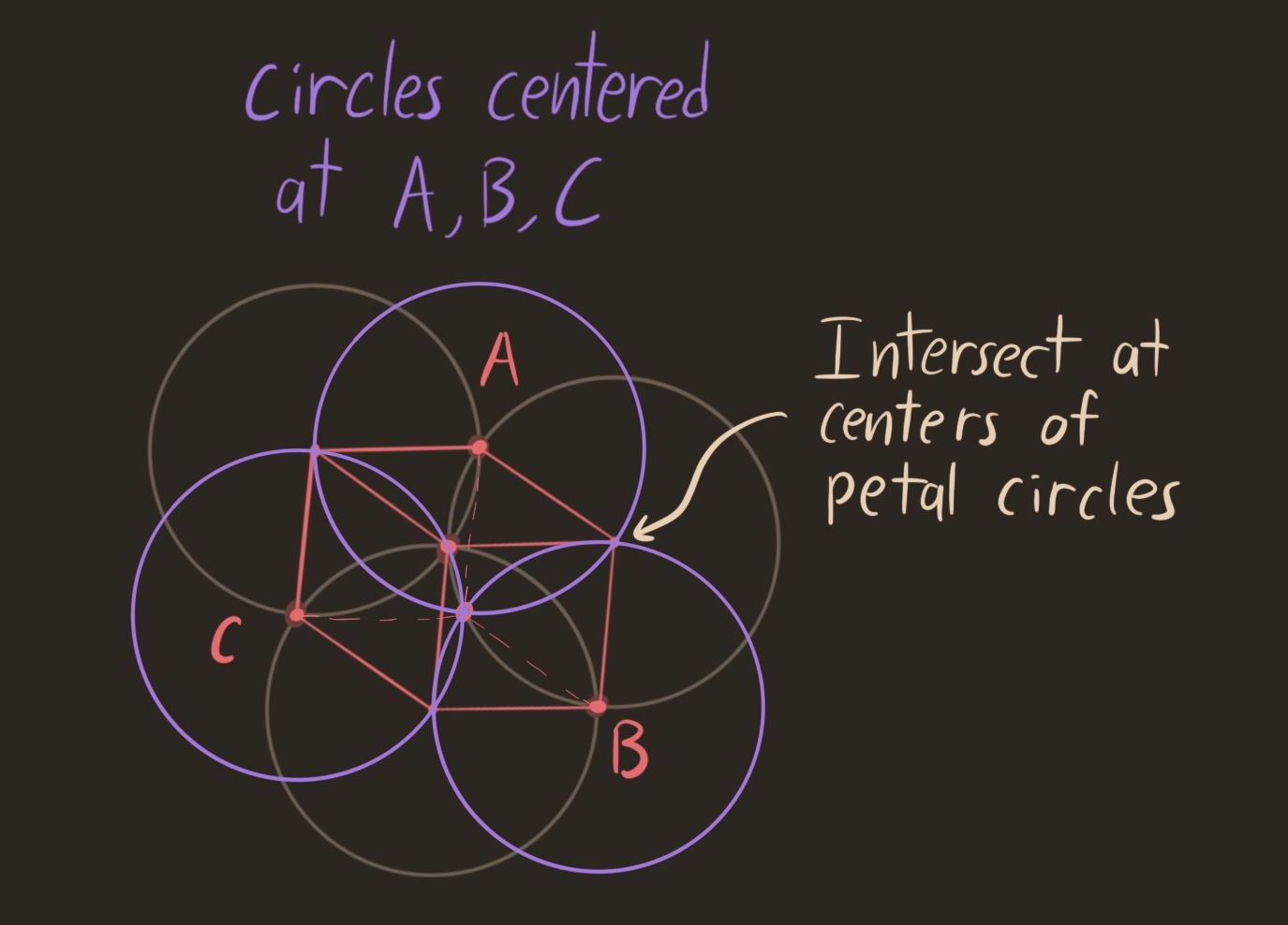
A Dual contorted seed of life

These circles intersect all together at the back corner of the cube. They also intersect at the centers of the original petal circles, like the other side of the same coin. While the original petals came from the front of the cube, these new petals come from the back of the cube. Unless the front and back of the cube line up, these two sets of petals have different governing circles. Hidden behind every contorted seed of life, there is another contorted seed. Try it yourself: Align both circles, and the two contorted seeds overlap to form a familiar sight. The seed of life returns in its sacred glory, with a equilateral hexagon as a treat.

The contorted seed of life is not a perversion of the seed, but instead a realization that the seed originates from a three dimensional arrangement of spheres around a central cube. In the sacred geometry playbook, this arrangement of eight spheres is called the Egg of life. By changing the third dimensional perspective, the seed of life splits into two contorted seeds.

Here’s a 3D model I made, a cube with flexible vertices. I recommend this, its a fun object to play with. In the first picture, I show a 3D view of the cube standing up. After flattening the cube, I get the second picture. The two vertices on the inside of the outer hexagon are the centers of the governing circles for the two contorted seeds of life. In the last picture, I overlap both internal vertices. The two contorted seeds combine into one, the original seed of life. At the same time, the outer hexagon becomes equilateral.

A cube of sticks

A representation of the proof idea behind the contorted seed of life. To make this, I layed each vertex flat with 120 degree angles, and sandwiched it between 2 layers of duct tape. Then I trimmed off the excess. This is a surprisingly strong way to make flexible joints.

Constructing the center of a circle with a pointless compass

Remember that the contorted seed of life is the ordinary seed of life when we start with the true center of the source circle. Once we have that, it is easy to construct a hexagon with a pointless compass. The seed of life and its dual together triangulate the center. Unfortunately, the dual seed is constructed assuming we know the center of a circle. Without that, the dual seed is inaccessible.

Luckily, I found a way to construct the center of the source circle. The only trouble is, I’m not sure why it works… Here’s my construction. In the figure below, The original source circle is in red, the first layer contorted seed of life is in white. We will expand the flower one more layer, here given by the purple circles. To do this, we use our straightedge for the first time. Extend the line AO until it hits the source circle and the opposite pedal circle. These two intersections will be cocircular with both $B$ and $C$.

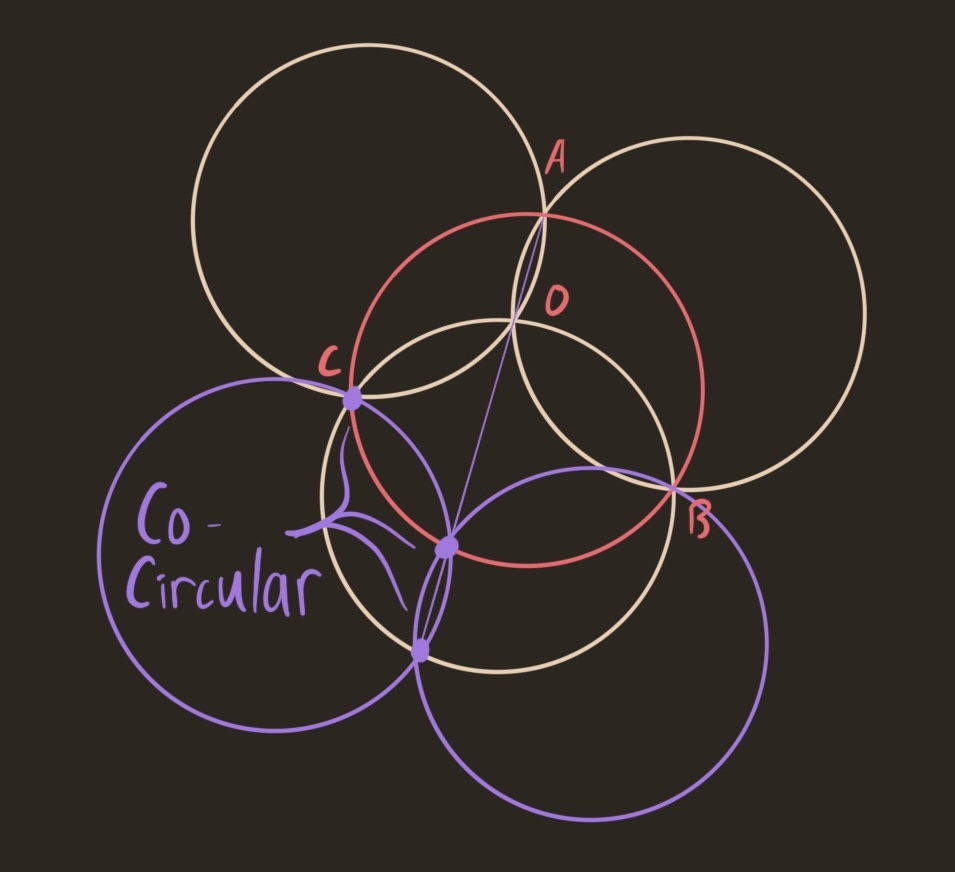
Repeating this construction everywhere we can, we grow a new layer in the contorted flower of life

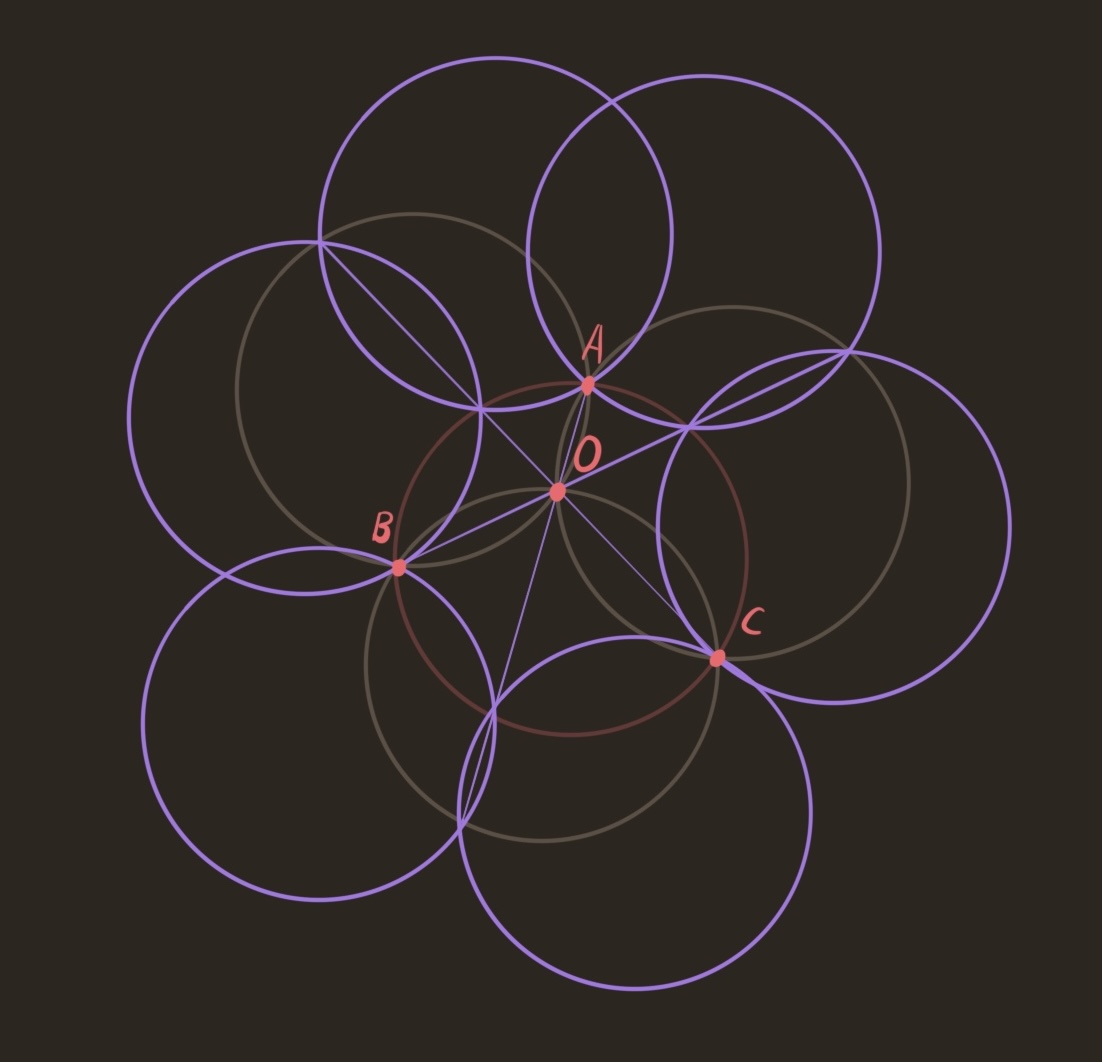
The second layer of the contorted flower of life.

We constructed the purple ring using three lines (AO, BO, CO), which became the lines connecting the two intersections of adjacent circles. But, we only used half the overlaps. Following the philosophy of the cube, we expect that of the six overlaps, half of them determine the contorted seed of life, and the other half determine the dual contorted seed of life. In the dual seed, the role of $O$ is played by the center of the source circle. So, we are lead to consider the three other lines (drawn in green below).

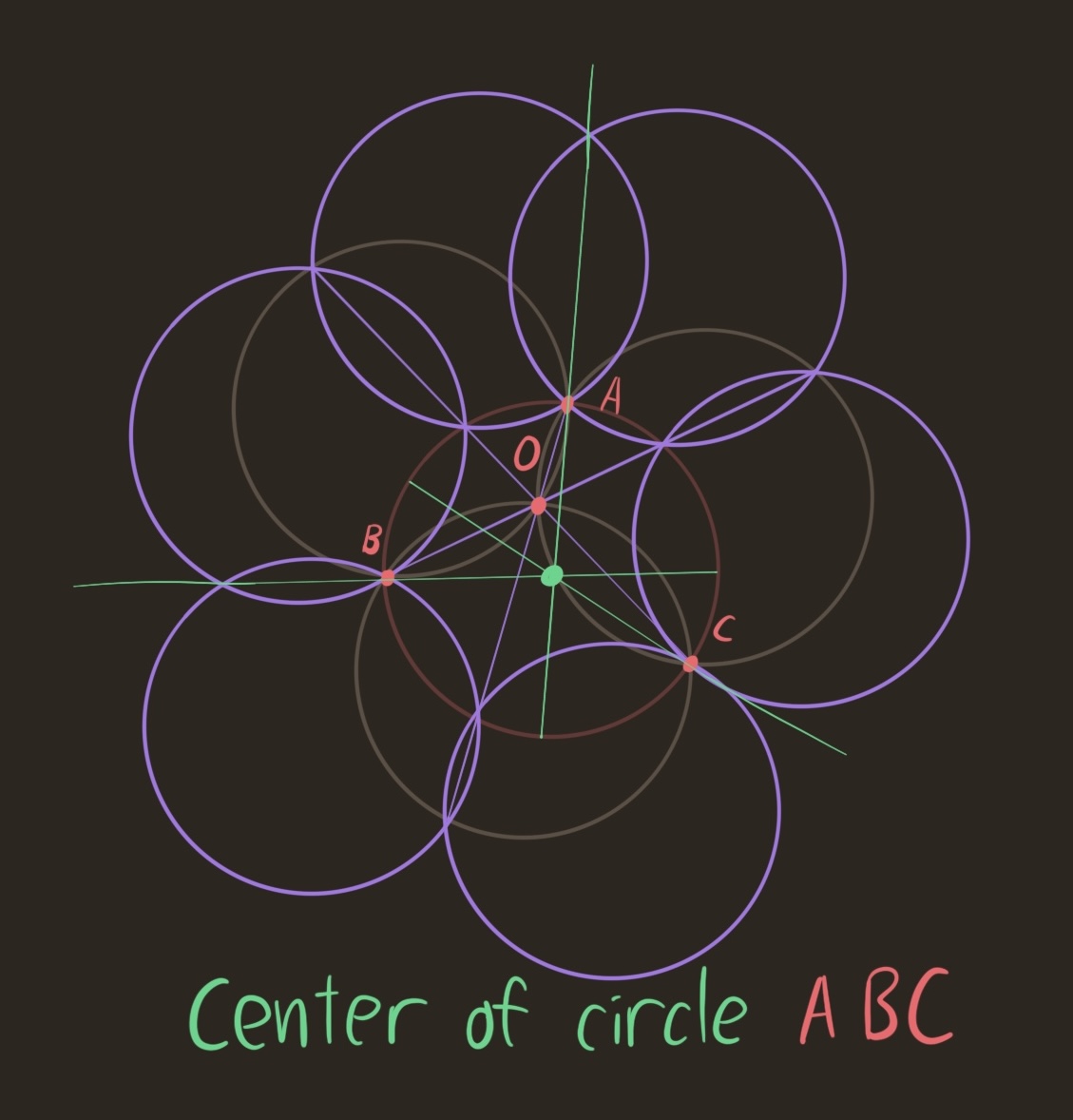
Construction of the center using a pointless compass

Empirically, the three lines meet at a point, which is the center of the circle ABC. See for yourself.

And this concludes my incredibly convoluted construction of an equilateral hexagon. If that isn’t cursed geometry, I don’t know what is.

There are simpler constructions of the center of a circle using a pointless compass. See this stack exchange post. For my purposes of constructing the center in my drawing app, I can abuse tangencies (usually not allowed in compass straightedge constructions). This is the “egg of life” construction:

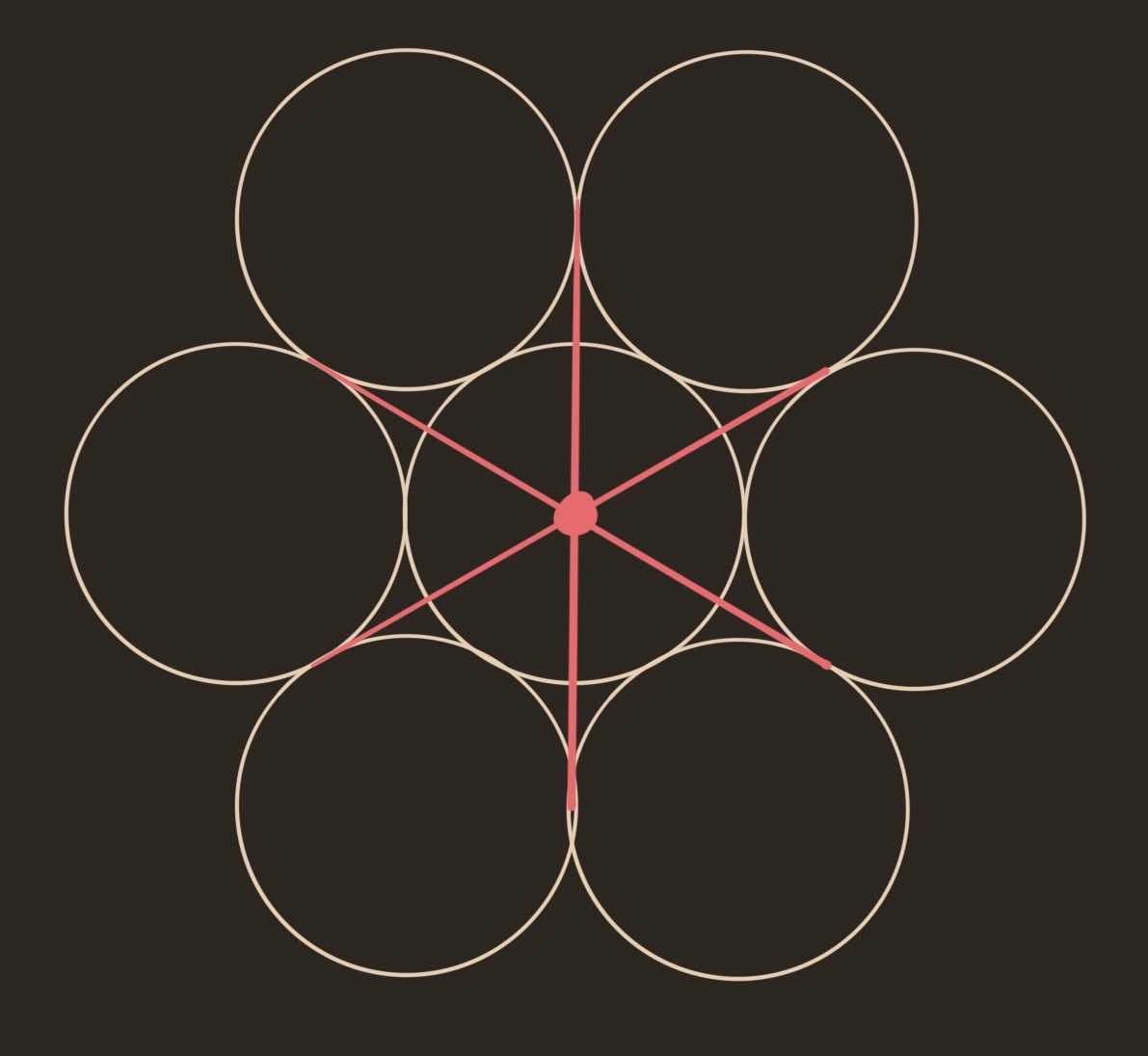
The egg of life

Beyond the second layer…

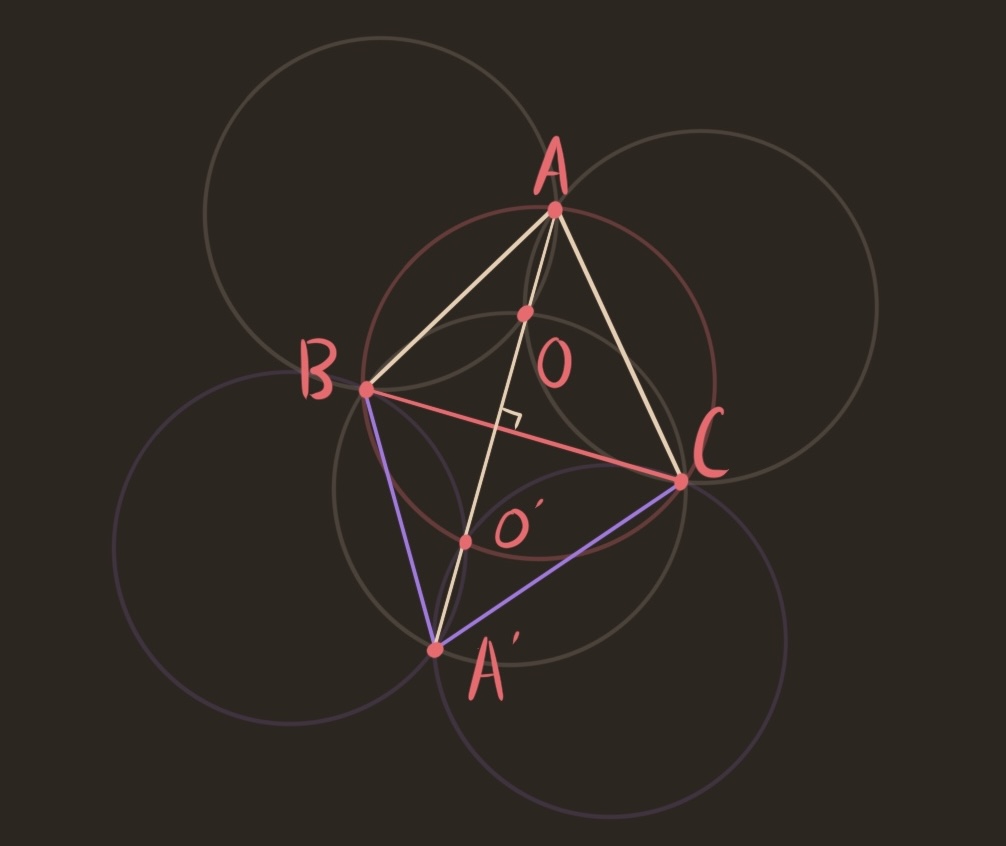
What if we tried to go farther? Build another layer of the flower, expand out and out? If you try to do this with circles, it quickly becomes untennable. Instead, we change perspectives, and think of the contorted seed of life through its triangle $ABC$. After all, any triangle can be scaled to be the triangle of a seed of life with unit radius. This is the perspective of the Johnson triangle. The center of triple intersection, it turns out, is the intersection of the altitudes of the triangle, also known as the orthocenter.

To extend the seed of life in the direction of $B$ and $C$, we reflect the figure around $BC$. The new triple intersection $O’$ is the reflection of $O$, and the new double intersection point $A’$ is the reflection of $A$.

So to extend the seed, layer by layer, we take our original triangle and repeatedly reflect it across its own edges. If we do this with a equilateral triangle (as in the original seed of life) we get a hexagonal grid. A contorted seed blooms into a horrifying yet beautiful cacophony of triangles. Try changing the initial triangle in the geogebra below, and see how the reflections fly about.

I suspect that, if the original triangle has irrational angles, then the points constructed from the full contorted flower of life will be Dense in the plane. Yet, for some specific triangles, the contorted flower wraps back into symmetry. Try to find one of these special triangles. This same repeated unfolding construction arises in the study of triangular billiards. The question is, if you move in one direction, unfolding every time you hit an edge, does your triangle ever return back to a translate of its initial state? Equivalently, does every triangular billiards table have a periodic billiards shot? This question is wide open for irrational triangles with obtuse angles, despite being studied for more than 400 years. That should give an inkling of the complexity hiding in the fully bloomed contorted flower of life.