Garden of mathly delights
Summary:
A landscape of different areas of math. This was done on commission as the banner for the youtube channel K-theory
Gallery
The mathscape
The full banner. To zoom in to different areas and get an explanation of what you’re looking at, see the other images in this gallery.
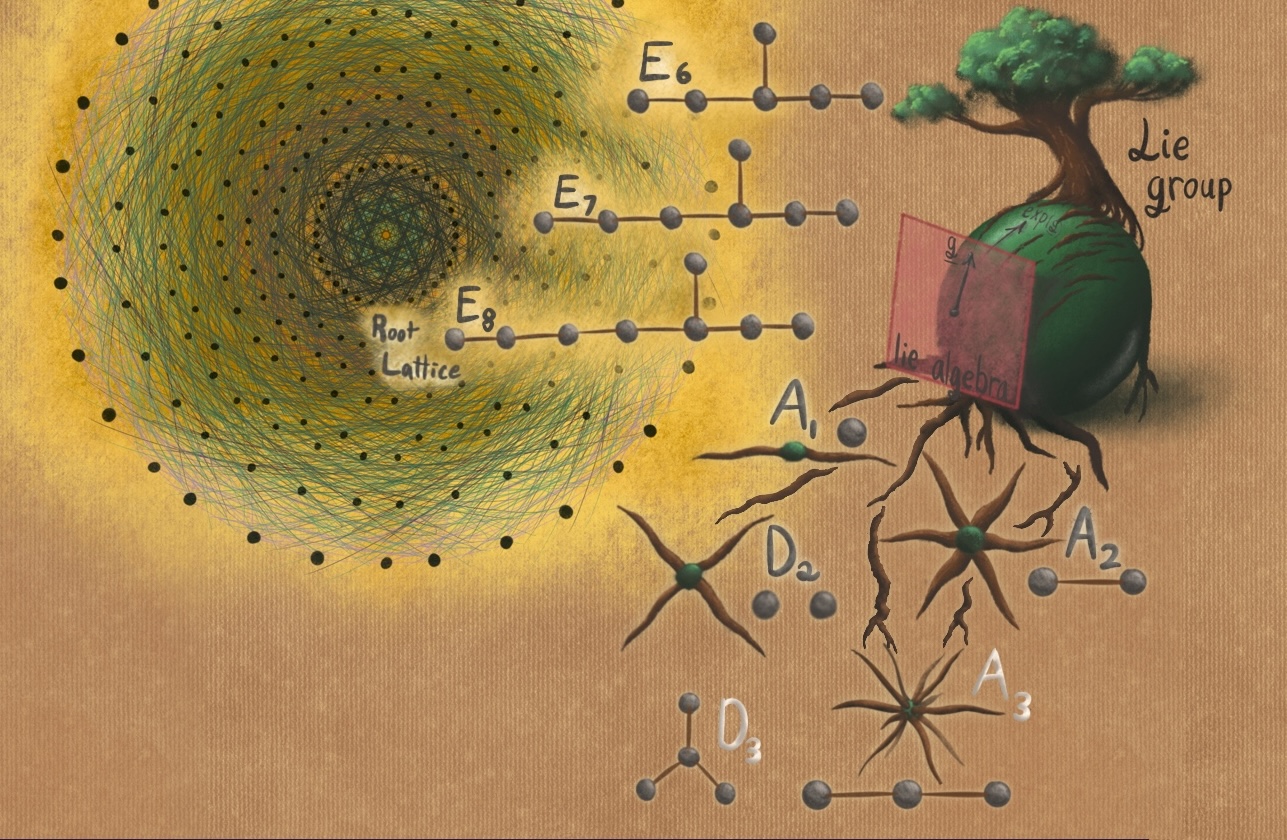
Lie theory
Some elements of Lie theory. I draw some root systems in the style of roots of a tree, and draw the lie algebra as the tangent space to the lie group. I also draw something reminiscent of the classic drawing of the E8 root lattice.
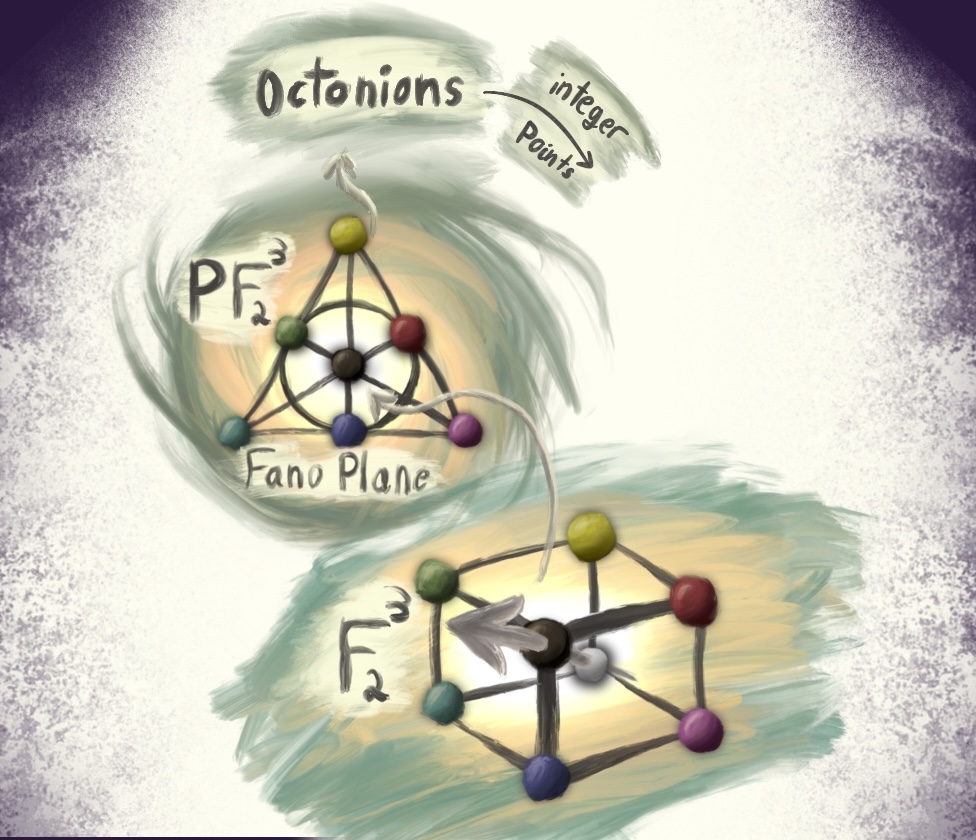
The fano plane
This is a depiction of the Fano plane, and its relationship with the finite projective plane over $\mathbb{F}_2$. The fano plane describes the multiplication structure on the integer points in the Octonions.
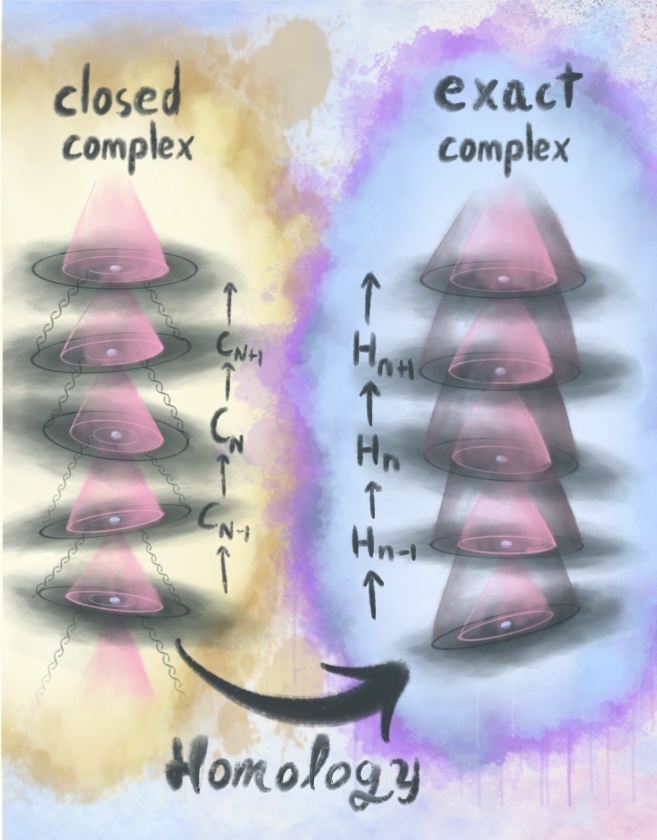
Homology
This shoes the chain complexes arising from topology, as a set of vector spaces (the circles) with maps including one in another. The chain map squared is equal to zero, which is depicted on the left as the chains moving inside the pink area. On the right, I draw the homology built from the chain complex.
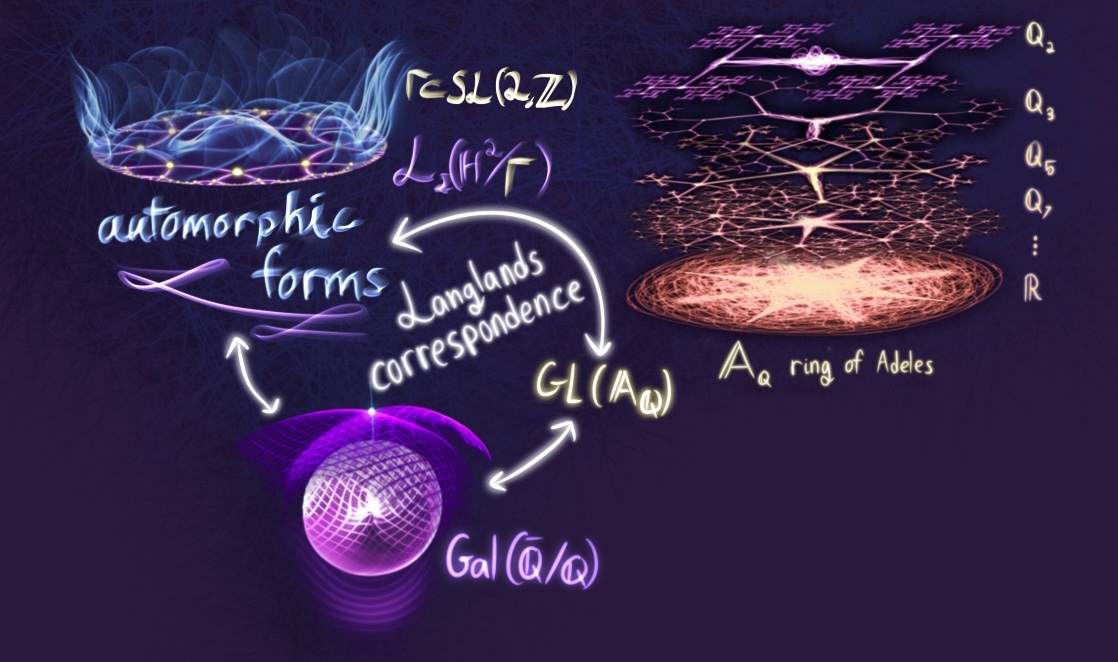
The langlands program
Depicts three sides of the Langlands program. Automorphic forms (the spectral side, left) are related to linear maps on the ring of Adeles (the representation theoretic side, right). These are bound together by Galois theory (bottom).
Differential geometry
A collection of surfaces from classical differential geometry, basking in a vaporwave manifold sunset.
The Klienscape
a prototype of the differential geometry landscape. It was lots of fun to design brushes for the grids, the clouds, and the sun.
Morse theory
A depiction of the morse decomposition. Given a function on a manifold, the critical points information gives a series of instructions for sewing together the manifold out of simple parts.
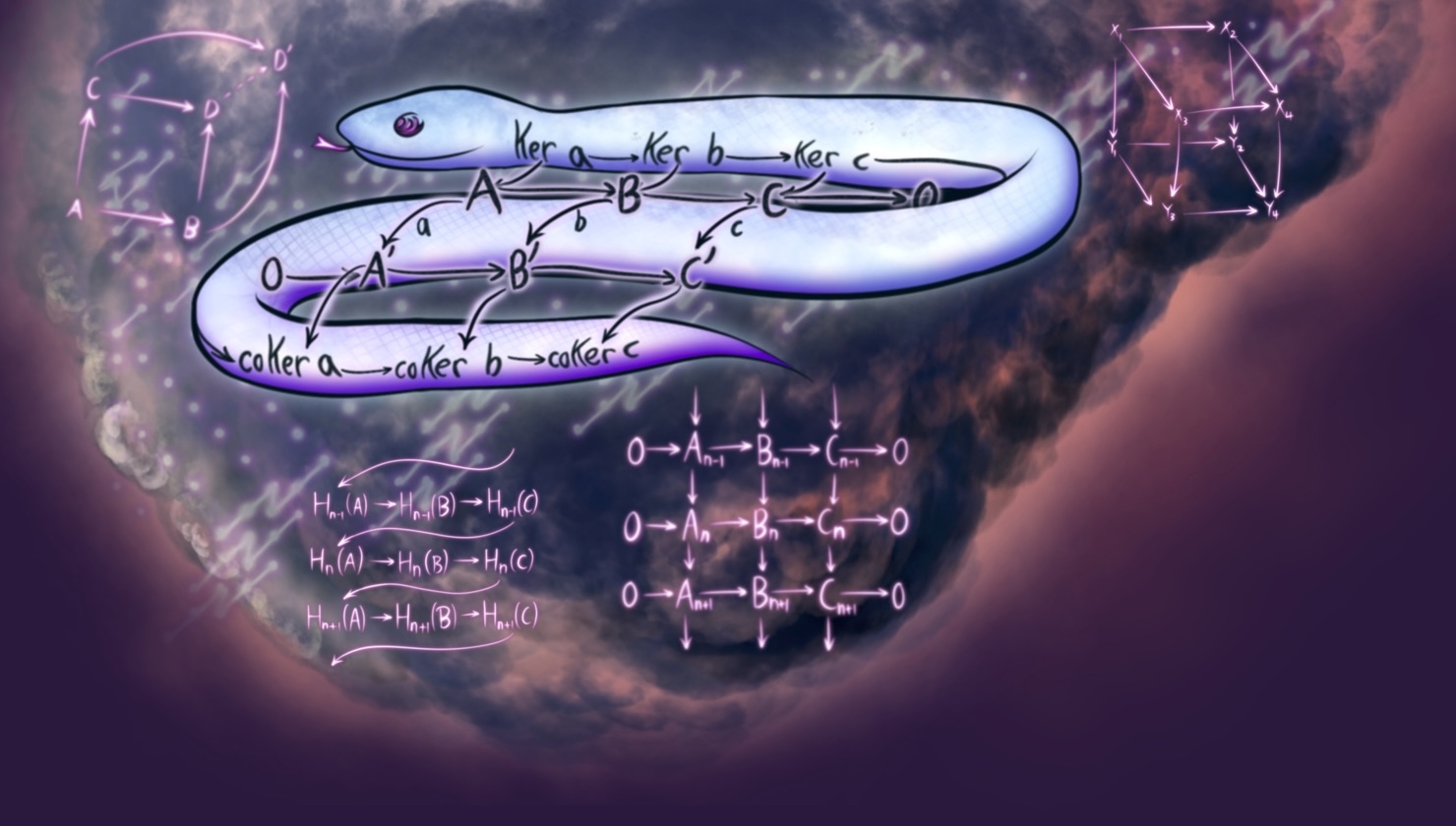
Homological Algebra
A depiction of several diagrams from homological algebra. Front and center, the snake from the eponymous snake lemma. In the background, there is the faint image of an adams spectral sequence.
Dynamical systems
A depiction of the circle doubling map, and related systems. on the right, we apply the circle doubling map to each pixel. The smooth image in the bottom transforms into static on the top, representing the chaos of the circle doubling map. In the background the Mandlebrot set looms. The Mandlebrot set probes the dynamics of the complex squaring map, which is a complexified version of the circle doubling map.
The tent map
A close up on the stack of pancakes from the dynamics section. This was made using the techniques from my playing around with gradient maps. Each layer is made by applying the tent map to each pixel from the layer below. Notice how the number of bands doubles each time, getting so dense that it dissolves into noise and chaos.
mathematical box of donuts
Some art style tests, rendering tori.