The mirror symme-tree
Summary:
The mirror symme-tree is a portrait of the field of math known as mirror symmetry. In the search for a theory of everything, physicists discovered mirror symmetry which posits that two different physical theories are dual to one another. For mathematicians, this duality builds an unexpected bridge between unrelated fields of math. The mirror symme-tree illustrates the mathematical structures and relationships from the eponymous field.
Math lives atop a scaffolding of physics. Physicists organize the world into a hierarchy of quantum field theories, which I conceive as a great tree. Mathematical critters populate the branches, reflecting the structures and symmetries of the underlying physics. There is a mysterious duality between the wide-spreading branches, hinting at an unexpected kinship between critters living in disparate areas of math. Welcome to the mirror symme-tree.
 |
|---|
| The mirror symme-tree |
Let’s take a look at the physics behind the trunk of the tree. Physics is built by quantum field theory, but the theory describing our universe is hard. Exact results are fleeting. This contributes to a strained relationship with mathematics – if you manage to even define these things, you get a million dollars. Instead, we build a new universe, a toy model to poke and prod.
The easiest universes to understand are those with lots of symmetry. We add evil little versions of every subatomic particle, making our theory “supersymmetric”. The more symmetric particles we add, the simpler the universe is. Why no go all the way, and add 16 versions of every particle. This is enormously restrictive. Always unsatiated, we simplify even more by twisting the theory to be “topological”. in our constructed universe, the particles do not move. Nothing changes as you move throughout time. Its history is locked in stone from the outset, controlled by nothing but the shape of the universe. There is no physics here. The great machine of quantum field theory toils and whirs in this facsimile of a universe, and leaves us with a single number. The partition function.
 |
|---|
| The starting quantum field theory for today, $4D, \mathcal{N}=4$ supersymmetric yang mills theory |
Even though the universe is boring, this partition function is very interesting, probing the data used to define the theory. To describe a quantum field theory, we need to choose a “field”. Take the electric field, which we describe using the potential energy. The field is determined by a real-valued function on spacetime. Instead, our field can be a functions on spacetime valued in some manifold with extra structures. This gives a geometric construction of a quantum field theory. The partition function from before gives geometric information about this manifold. Mathematicians would pay a pretty penny to know this information.
There are two ways to make a theory topological, the A and B twists. Physics predicts that every B-twisted theory has a “mirror”, and equivalent A-twisted theory. This “mirror symmetry” lets us compute an A-twisted partition functions using a B-twisted theory.
 |
|---|
| The twists are two, twisted branches spreading out from the central theory. Notice the calming swoops of the B-twist, compared to the harsh scraggles of the A-twist. The B-twist is often easier to work with. |
Consider a 2-dimensional universe. In an A-twisted theory, the fields are valued in a symplectic manifold (see my thread on twitter), and the partition function counts J-holomorphic curves, 2-dimensional soap films stretching across our symplectic manifold. In contrast, the fields in a B-twisted theory are valued in a complex manifold, and the partition function measures its topology (hodge theory). Can we use physics to help compute these numbers?
 |
|---|
| the 2D section of the mirror symme-tree. Notice how the “A-model” branch maps into “holomorphic curves” living in a symplectic manifold (the blob of leaves) |
Yes we can, and it’s a bombshell. Mirror symmetry says that every A-twisted theory has a mirror B-twisted theory, with the same partition function. Geometrically, every symplectic manifold has a mirror complex manifold. We can count J-holomorphic curves (hard) by constructing the mirror, and computing its topology (easy). Mirror symmetry builds an bridge between the mathematical continents of symplectic and complex geometry, which has ushered in a booming trade industry.
☡ Warning ☡: the “2D” in 2D mirror symmetry is about the dimension of the spacetime, not the auxiliary symplectic manifold. The theory is 2 dimensional because it probes the manifold of fields with a 2 dimensional curve. Similarly, 3D mirror symmetry studies special 3D sub-manifolds.
 |
|---|
| the 3D section of mirror symmetry. Note that now the A-model maps into “Feuter”. This describes the special 3D submanifolds of interest. |
In every dimension up to 4, there are analogous quantum field theories. If your 4D universe has a border, then a 4D theory induces a 3D theory known as the boundary theory. This itself has a 2D boundary, and so on to a point. The information of all these boundary theories is contained in the 4D partition function.
 |
|---|
| the central trunk of TQFTs. Notice how each layer is the boundary of the tree above, losing one dimension each time |
Each dimension up has its own A and B twists, which count maps of spacetime into manifolds with ever increasing structure.
- 1D quantum field theories map into Riemannian or complex manifolds
- 2D quantum field theories map into Kahler manifolds (both symplectic, Riemannian, and complex)
- 3D quantum field theories map into hyperKahler manifolds (which are based on the quaternions)
 |
|---|
| Utop the central trunk, there are branches at each dimension for A and B twists. Each dimension has its own target manifold, the blob of leaves in the center of the tree. As we move up the tree, the geometric structure on the target leaves gets more and more complicated. In 1 dimension, the A and B twists target different manifolds from eachother. |
The partition function is more than just a number, for It encodes information of counting maps with boundaries. Secretly, it is governed by a mountain of algebraic structure.
- in 1D, the partition function comes from a vector space
- in 2D, it comes from a category
- in 3D, a 2-category.
- and so on
For example, remember how the 2D A-twist counts maps into a symplectic manifold? The full information counts maps with specified boundary conditions. In a symplectic manifold, the correct boundaries of a J-holomorphic curve are nice sub-manifold called Lagrangians. The category associated to this quantum field theory is called the Fukaya category, and it counts strips between two specified Lagrangians.
 |
|---|
| 2D mirror symmetry again. The Lagrangians or coherent sheaves are rendered as mushrooms living on the tree. After all, they are boundary conditions. The A and B models are sigma models, mapping the central 2D trunk into the bulk of a symplectic manifold. The branches themselves splay out in a 2D way into the leaves, ending on the mushroom boundaries. On the B-side, the branches converge in a point. On the A-side, an inchworm stretches a 2D web between the two boundary conditions. This is the ‘strings’ of string theory, stretching between two Lagrangain branes. |
We can reduce dimension in another way, wrapping one direction into a vanishingly small circle (Dimensional reduction). This shadow of the original theory is often more accessible, and gives a whole new tree with its own relationships.
 |
|---|
| In dimensional reduction, one direction is wrapped into a tiny circle. When we say string theory has “tiny extra dimensions”, this is what we mean. |
If we probe a 3D theory with little vortices (the acorns), and send them down to the shadow, it quantizes the manifolds defining the theory. Mirror symmetry manifests as an equivalence of the categories of these quantizations (See this paper). These little snakes hail from from geometric representation theory. They represent sheaves living on the shadows of two manifolds associated to a 3D theory. These manifolds are called the Higgs and Coloumb branch. 3D mirror symmetry predicts these manifolds are dual to one another, a strange relationship called symplectic duality. All this is a 2D shadow of true 3D mirror symmetry.
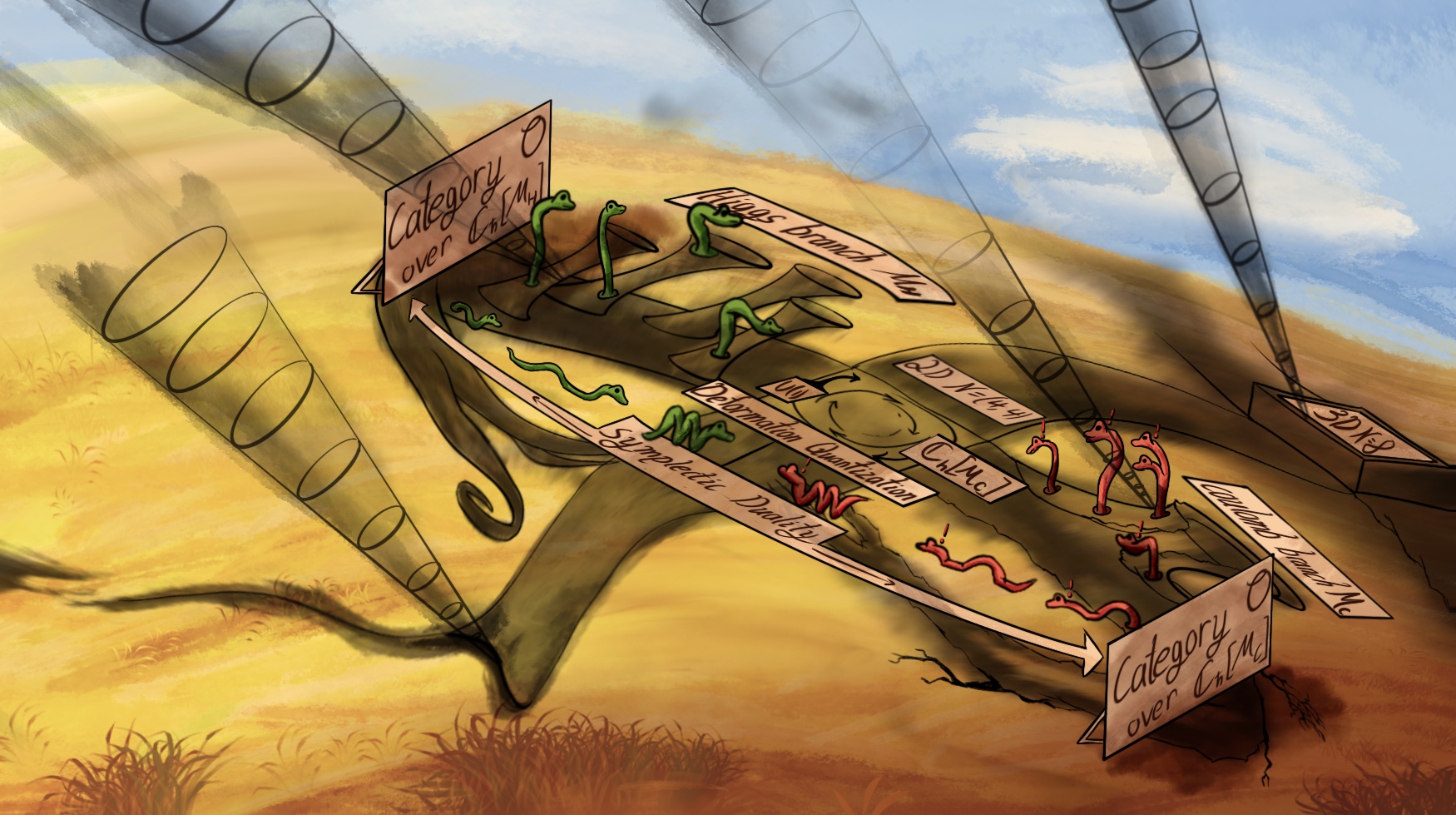 |
|---|
| The 2D shadow of 3D mirror symmetry. |
If we took a shadow again, then the 4D theory would become 2D. Here, mirror symmetry predicts the geometric Langlands correspondence, a geometric instantiation of the perhaps widest reaching research program of modern mathematics.
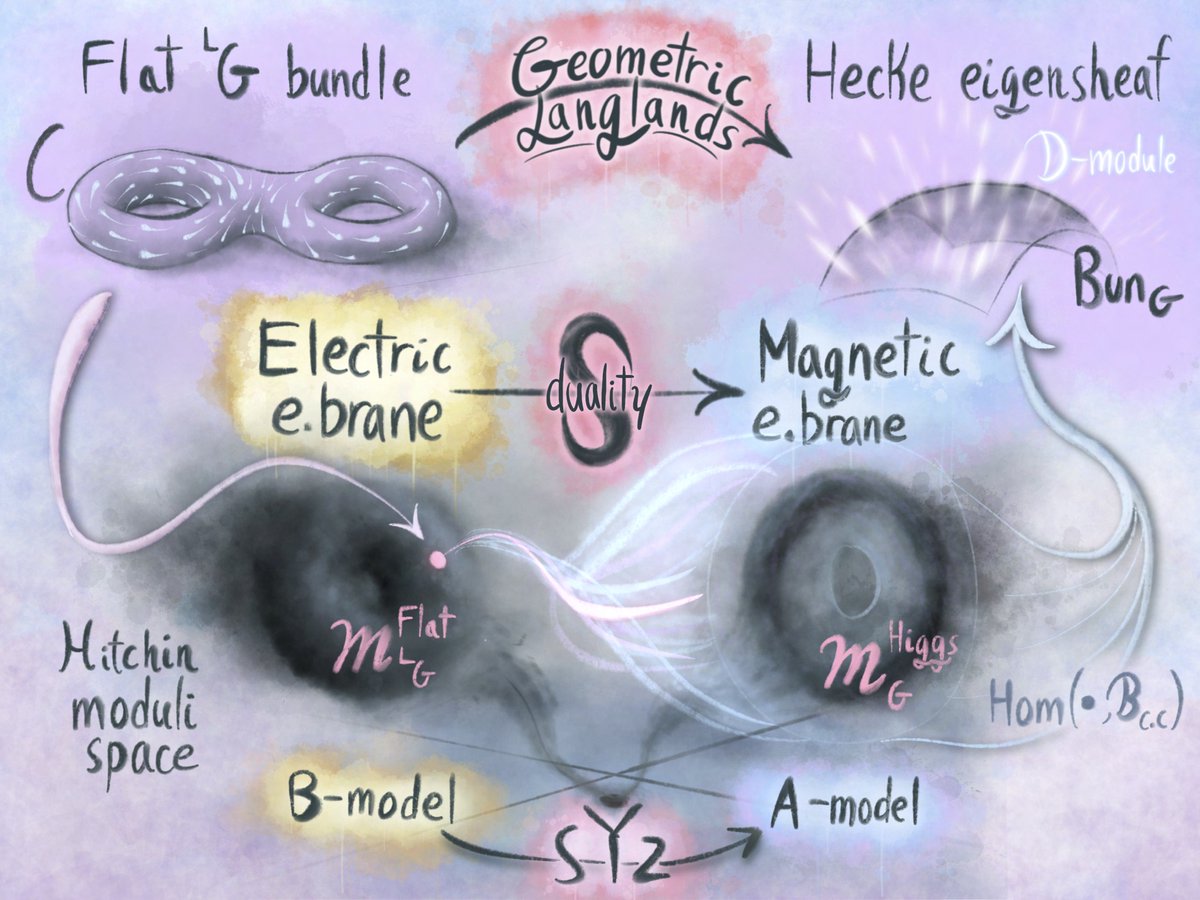 |
|---|
| A flowchart showing the physical interpretation of the geometric Langlands correspondence. This image came from my talk, linked here |
There are many more relationships, some drawn and most not. This microcosm shows the power of physics in math: Organizing ideas, tying together fields, suggesting conjectures using a separate intuition. Physics does shockingly good at its job.
Geolocation
This art was commissioned by Justin Hilburn to explain his research program, and its particular perspective on the field. The picture appears on his website.
This also appeared in:
- The Intersections exhibition at the Seattle Universal Math Meuseum (SUMM)
- Math Art exhibit at MathFest, August 2025
- The image for the Geometric representation theory and 3d mirror symmetry conference at SLMath, Fall 2025
Gallery
The Mirror Symme-tree
The full mirror symme-tree

