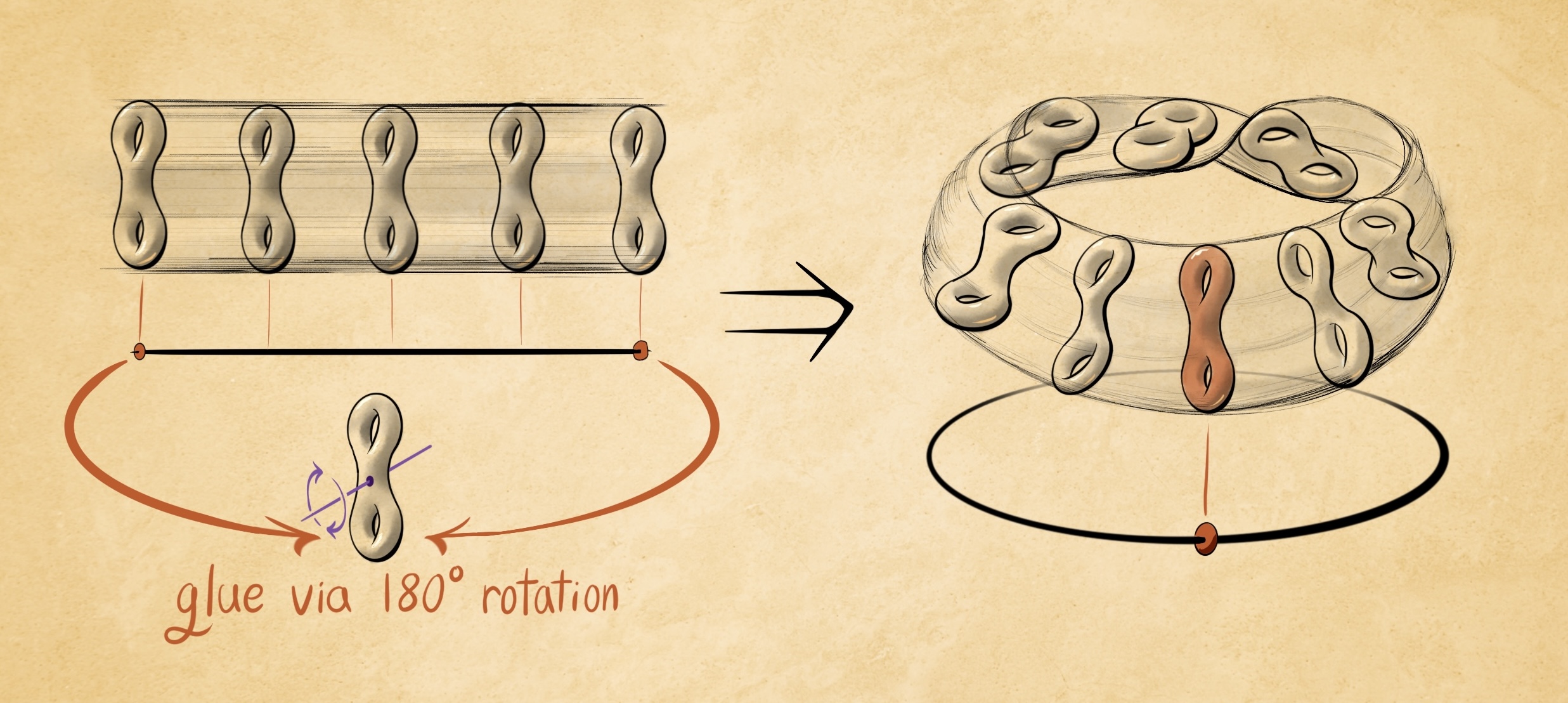
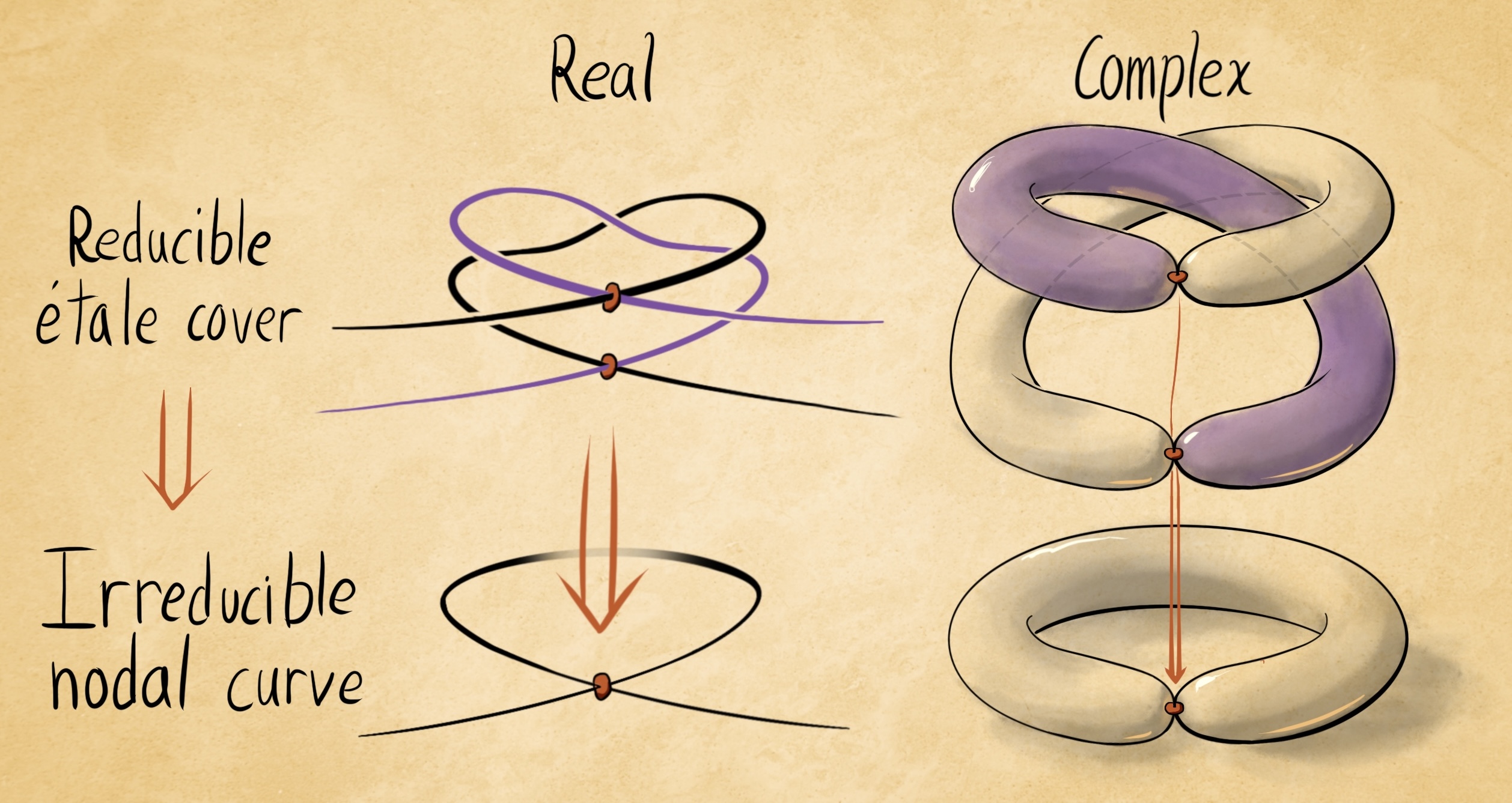
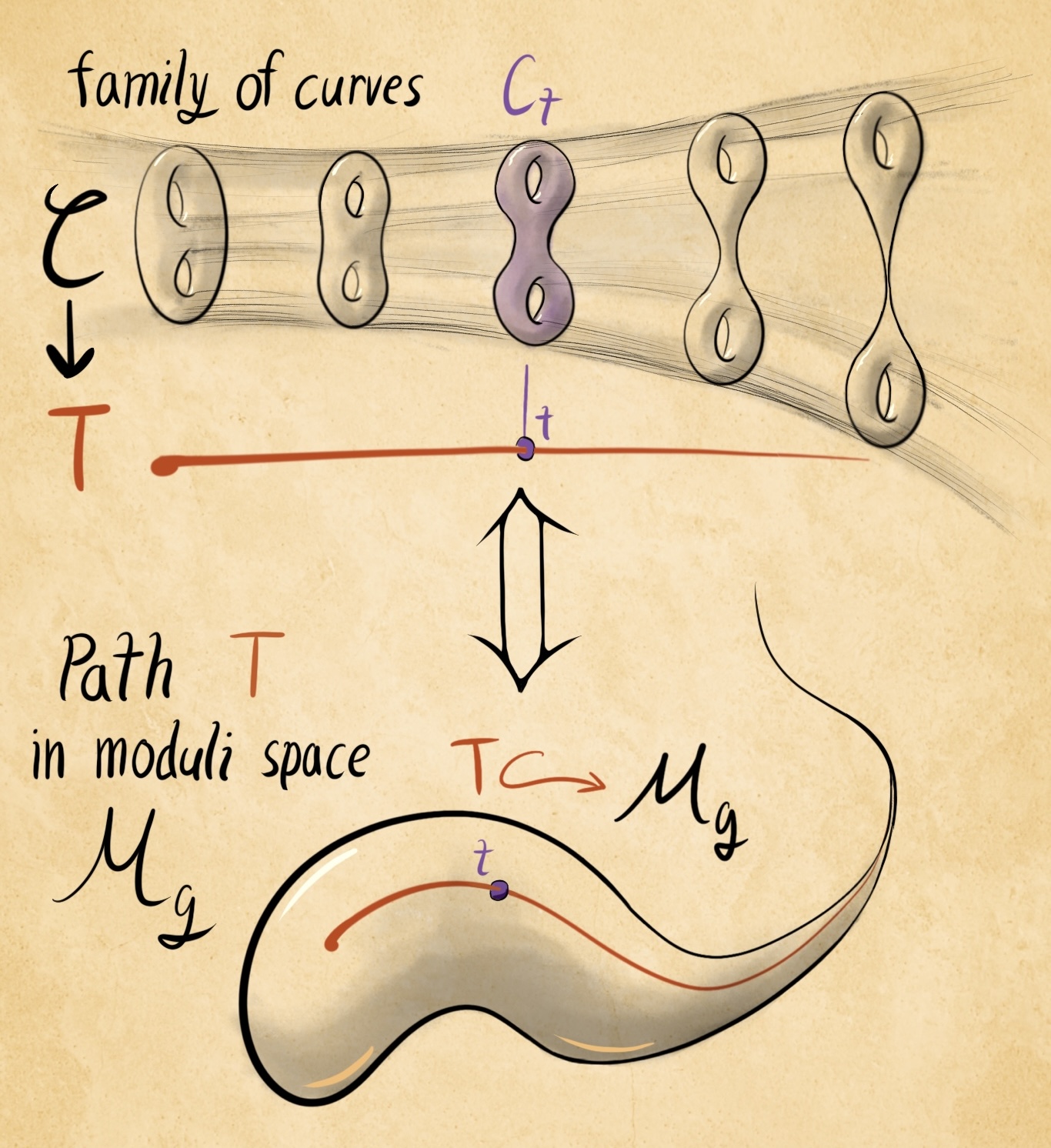
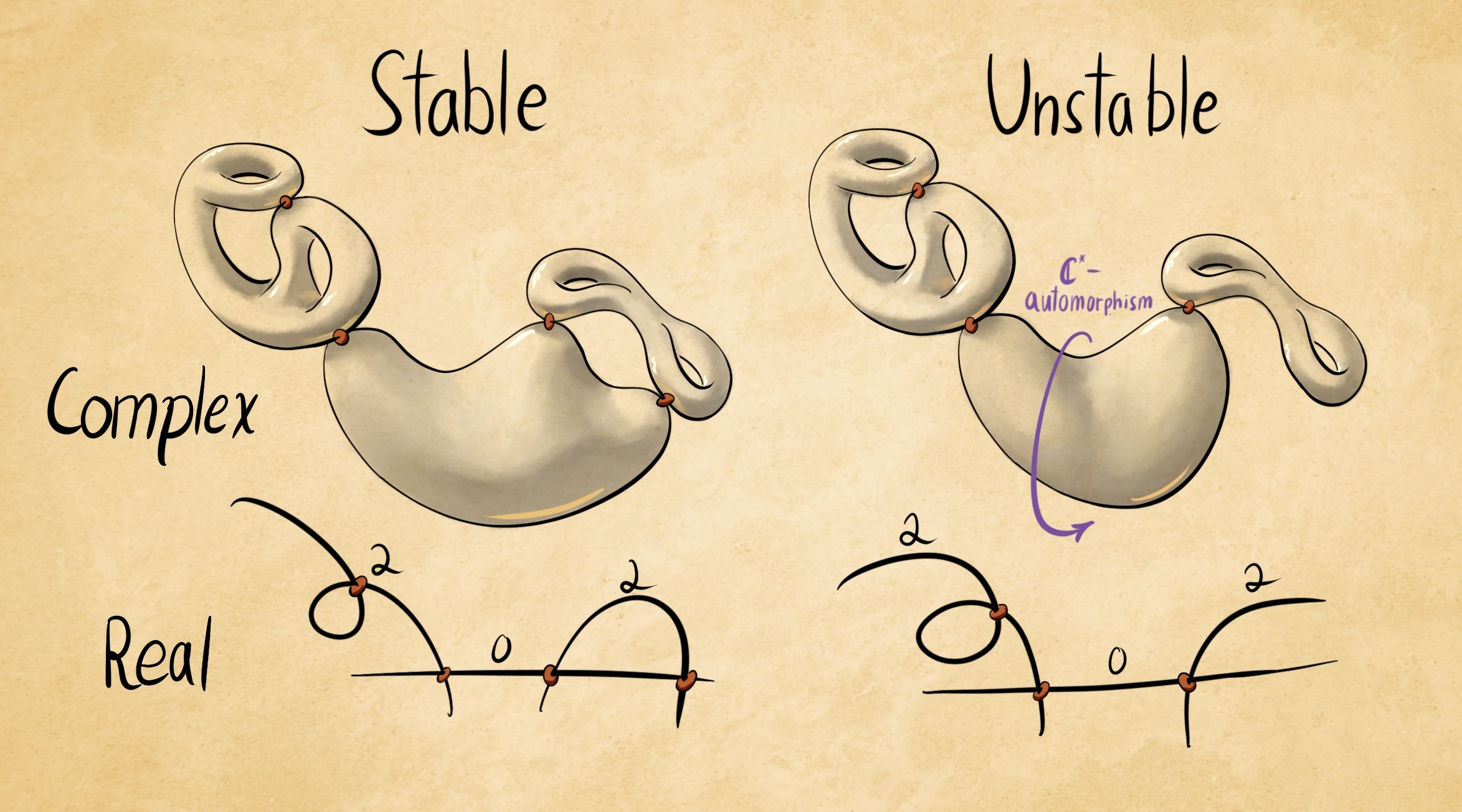
Stack drawings
Summary:
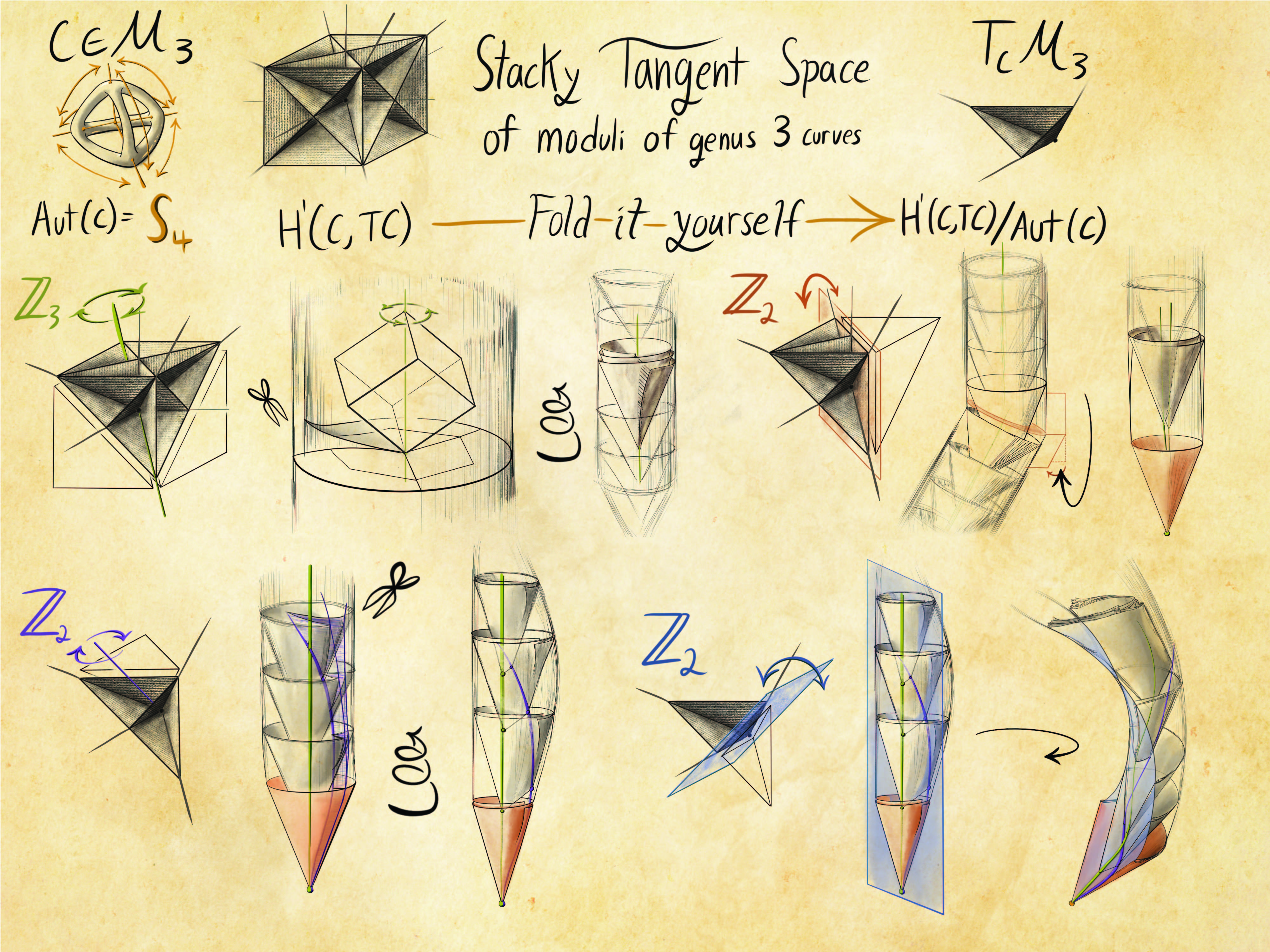
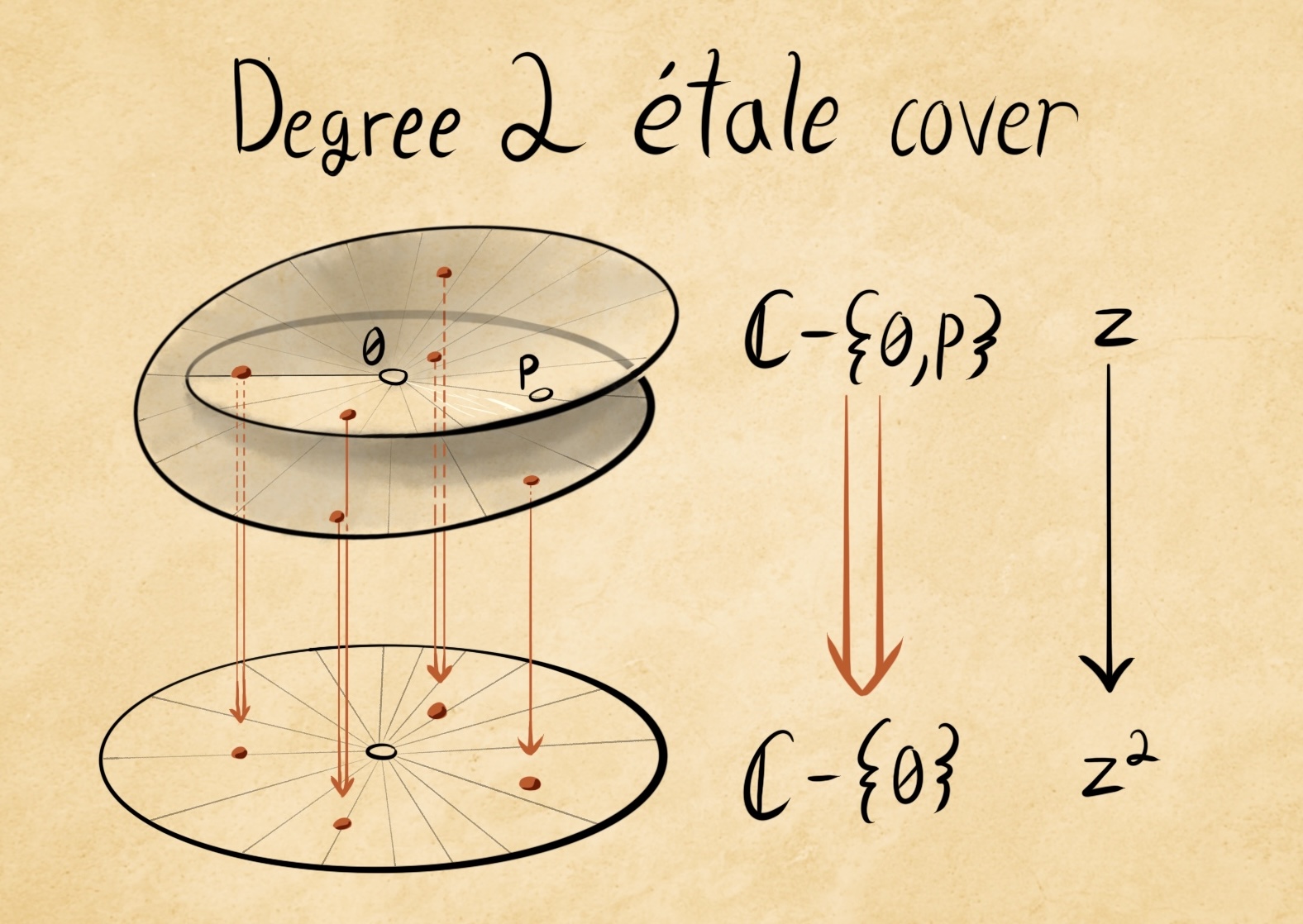
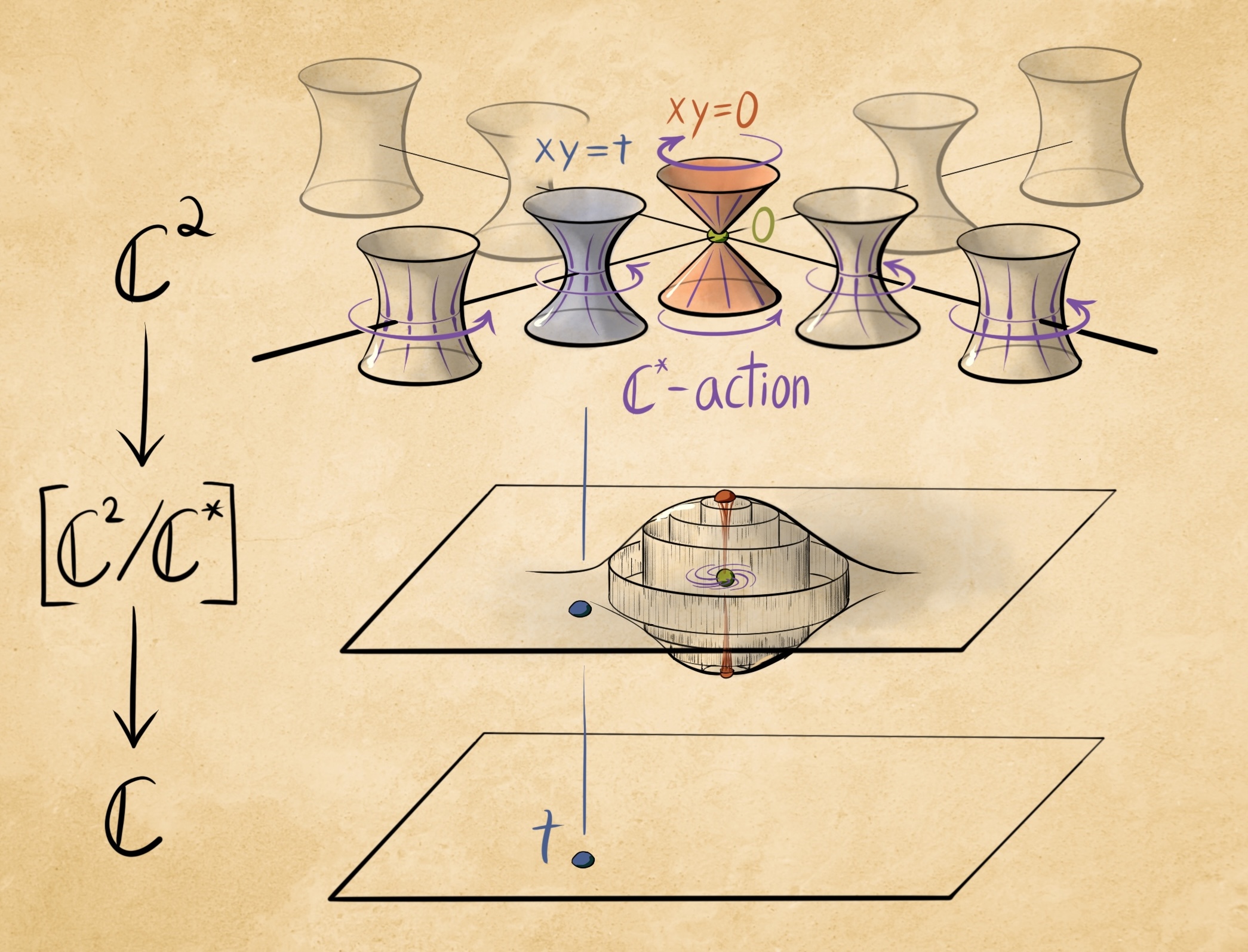
Drawings of stacks. These figures were drawn on commission for Jarod Alper, for his paper Evolution of Stacks and Moduli.
Gallery
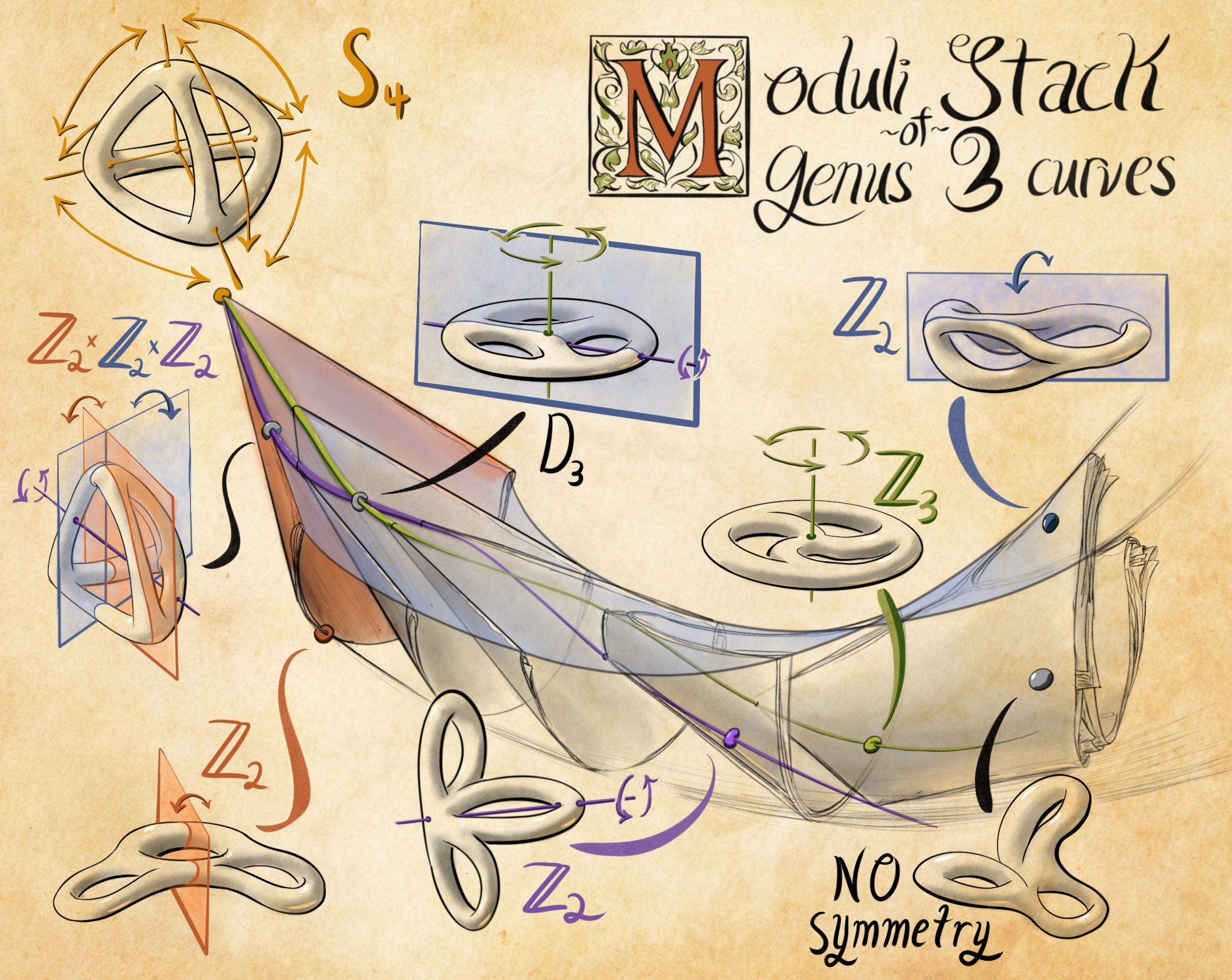
Moduli stack of genus 3 curves
Drawing of a subset of the moduli stack of genus three curves, showing how how the loci of points in the stack with certain automorphism groups might interact. As we move from the top left to the bottom right, we go from more symmetric to less symmetric curves. Each symmetry has its own locus, drawn in its own color with representative curves drawn alongside. From the top, we have:
- $S_4$ tetrahedral symmetry, drawn in yellow
- $\mathbb{Z}_3$ rotational symmetry, drawn in green.
- $\mathbb{Z}_2$ reflection symmetry, drawn in orange.
- another $\mathbb{Z}_2$ reflection symmetry, drawn in blue.
- $\mathbb{Z}_2$ rotational symmetry, drawn in purple.