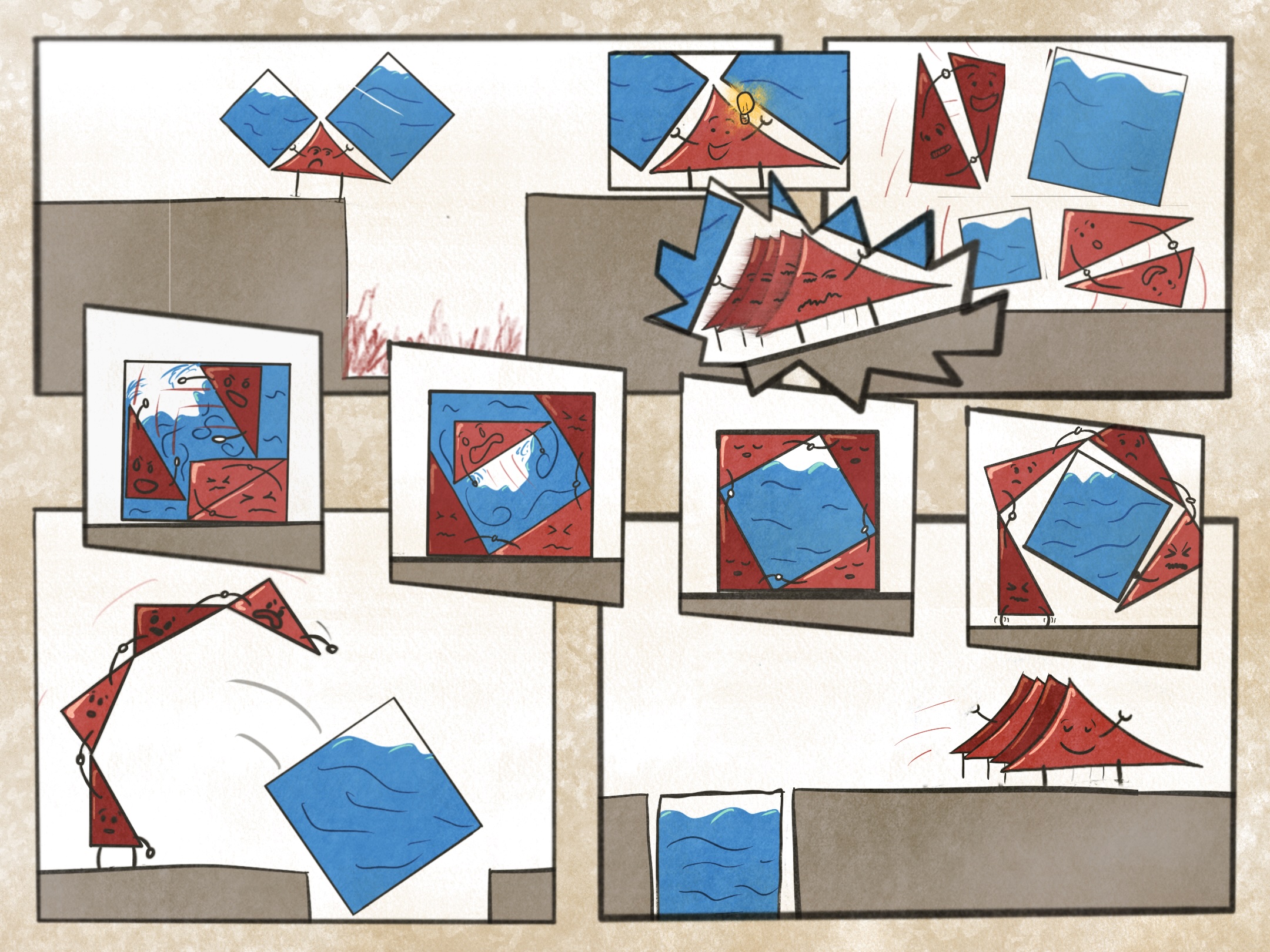
This is a page from a comic I never finished about universal bundles and classifying spaces. We follow the Queen of the grassmen, needing to organize her subjects, a field of grass growing on a manifold. The grass grows every which way, and the queen needs a way to see if the blades can be made to all line up. Can we detect wether a real line bundle (the blades of grass) is trivializable? So the queen toils to construct the classifiyng space of real line bundles, the infinite real projective plane. By lining up her kingdom according to the orientation of each blade of grass, she can topologically detect if the line bundle formed by the blades is trivial.

In this page, we see the queen marveling at the edifice of the ininifte real projective plane she just constructed. At the bottom it is just a point. Then, a circle is attached. Then, a disc is attached to that circle wrapping around twice. Then, a 3-disc, whose boundary sphere wraps around the 2D disc twice. And so on, forever and ever, diminishing into the haze of infinite dimensions. This visualizes the CW complex structure of one construction of infinite real projective space.

A proof-without-words of the pathagorean theorem. The goal was to turn the mathematical insights into charecter beats for our little triangle guy.